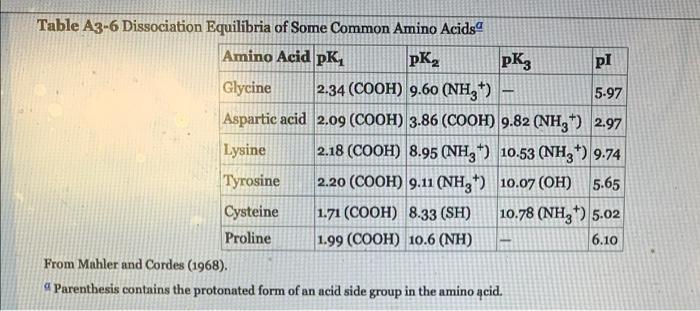
here is table A3-6 :
please solve all questions.
Aspartic acid has two carboxyl groups and one amide group that can each undergo an acid dissociation (see Table A.3-6 in the book). When solving this problem, let A represent the fully dissociated form of the acid in which both carboxyl groups are in their negatively charged form COO and the amide group is in its uncharged form NH2. Other forms of the acid can be represented by adding H* groups to A. For example, the zwitterion will can be represented by , (a) Write the sequence of dissociation equations for H,A+, HA and HA that progressively occur when an aspartic acid solution initially at a very low pH is titrated with a strong base until it reaches a very high pH. (b) Write the equation relating the concentrations of charged aspartic acid species at the isoelectric point. (c) Let Ki. K2 and 63 represent the equilibrium constants for the dissociation of HA', H,A and HA respectively. Write the formulas for these dissociation constants in terms of species concentrations. (d) From the results of (b) and (c), derive an equation for Cr at the isoelectric point in terms of the ki, K2 and K. (e) Using the values of pKj=-logk =1.88, pK2=3.65 and pK3=9.6, solve this equation for C. numerically and obtain the value of pH at the isoelectric point. Table A3-6 Dissociation Equilibria of Some Common Amino Acids Amino Acid pK, pKz pi Glycine 2.34 (COOH) 9.60 (NH4*) 5.97 Aspartic acid 2.09 (COOH) 3.86 (COOH) 9.82 (NH3) 2.97 Lysine 2.18 (COOH) 8.95 (NH3) 10.53 (NH3*) 9.74 Tyrosine 2.20 (COOH) 9.11 (NH) 10.07 (OH) 5.65 Cysteine 1.71 (COOH) 8.33 (SH) 10.78 (NH3*) 5.02 Proline 1.99 (COOH) 10.6 (NH) 6.10 From Mahler and Cordes (1968). a Parenthesis contains the protonated form of an acid side group in the amino acid. Aspartic acid has two carboxyl groups and one amide group that can each undergo an acid dissociation (see Table A.3-6 in the book). When solving this problem, let A represent the fully dissociated form of the acid in which both carboxyl groups are in their negatively charged form COO and the amide group is in its uncharged form NH2. Other forms of the acid can be represented by adding H* groups to A. For example, the zwitterion will can be represented by , (a) Write the sequence of dissociation equations for H,A+, HA and HA that progressively occur when an aspartic acid solution initially at a very low pH is titrated with a strong base until it reaches a very high pH. (b) Write the equation relating the concentrations of charged aspartic acid species at the isoelectric point. (c) Let Ki. K2 and 63 represent the equilibrium constants for the dissociation of HA', H,A and HA respectively. Write the formulas for these dissociation constants in terms of species concentrations. (d) From the results of (b) and (c), derive an equation for Cr at the isoelectric point in terms of the ki, K2 and K. (e) Using the values of pKj=-logk =1.88, pK2=3.65 and pK3=9.6, solve this equation for C. numerically and obtain the value of pH at the isoelectric point. Table A3-6 Dissociation Equilibria of Some Common Amino Acids Amino Acid pK, pKz pi Glycine 2.34 (COOH) 9.60 (NH4*) 5.97 Aspartic acid 2.09 (COOH) 3.86 (COOH) 9.82 (NH3) 2.97 Lysine 2.18 (COOH) 8.95 (NH3) 10.53 (NH3*) 9.74 Tyrosine 2.20 (COOH) 9.11 (NH) 10.07 (OH) 5.65 Cysteine 1.71 (COOH) 8.33 (SH) 10.78 (NH3*) 5.02 Proline 1.99 (COOH) 10.6 (NH) 6.10 From Mahler and Cordes (1968). a Parenthesis contains the protonated form of an acid side group in the amino acid