Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Here is the problem transcribed: ' Considering the expression (1/(sqrt(1+ax)))-sqrt(1-x) where a belongs to the set of rational numbers and a does not equal 0.


Here is the problem transcribed:
' Considering the expression (1/(sqrt(1+ax)))-sqrt(1-x) where a belongs to the set of rational numbers and a does not equal 0. The binomial expansion of this expression, in ascending powers of x, as far as the term in x^2, is 4bx+bx^2, where b belongs to the set of all rational numbers.
PART A: Find the value of a and the value of b.
PART B: State the restriction which must be placed on x for this expansion to be valid.'

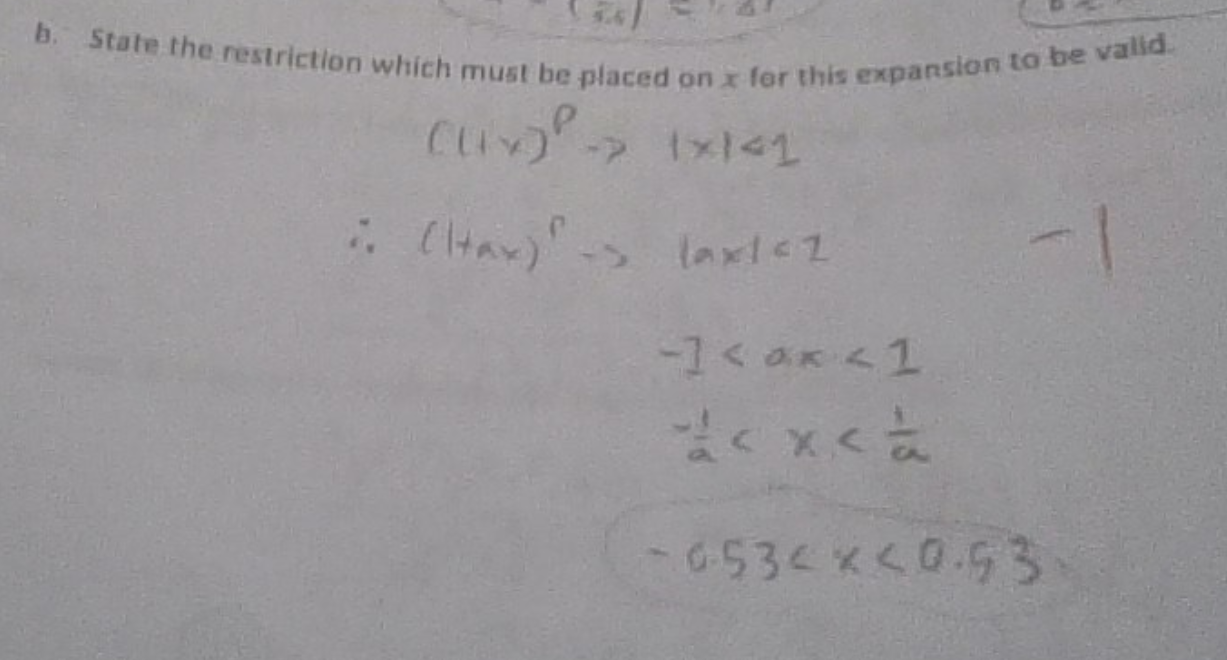
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


