Hi

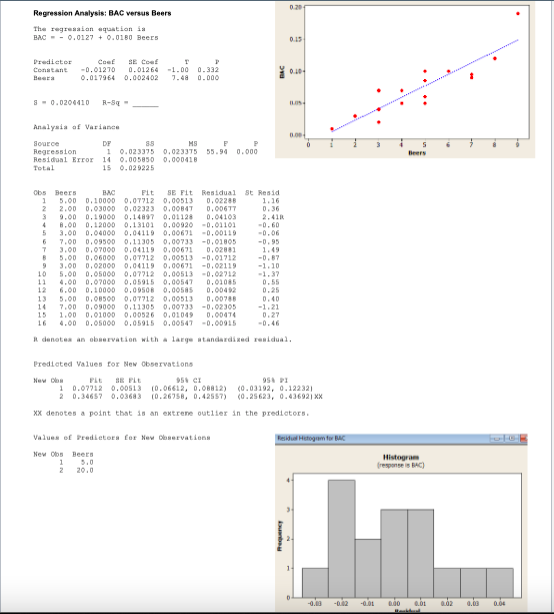
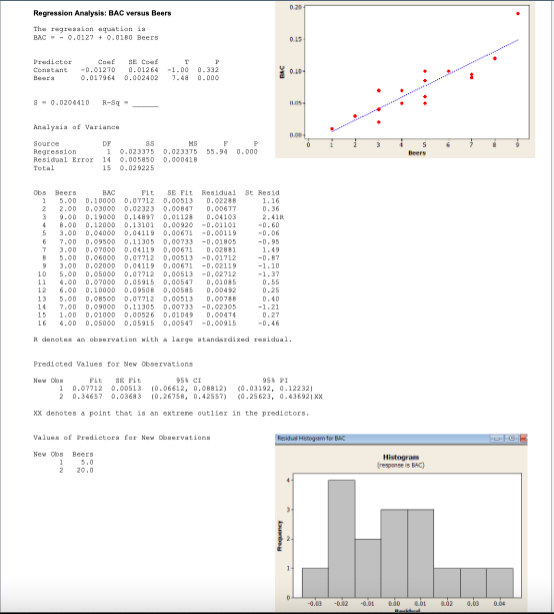
16 student volunteers drank a randomly assigned number of cans of beer. Thirty minutes later a police officer measured their blood alcohol content [BAC] in grams of alcohol per deciliter of blood. Data and computer output attached on next page. a) Find the least square line where BAC is dependent on Beers consumed. Interpret the slope. b) From the ANOVA table, Find and Interpret the r-squared statistic. c) Test the hypothesis that the beers consumed and BAC are correlated (a = .05) d) Find a 95% Confidence Interval for the mean BAC for a student who consumes 5 beers. el Would this model be appropriate for a student who consumed 20 beers? Explain. f) Joe claims that he can still legally drive after consuming 5 beers, The legal BAC limit is 0.08. Find a 95%% Prediction interval for Joe's BAC. Do you think Joe can legally drive? [) Residual Analysis 1. Look at the histogram of the Residual Errors. Do you believe the assumption for a Normal Distribution of Residuals Errors is satisfied? 2. We would expect the residuals to be random, about half would be positive and half would be negative. Check the actual residuals and compare the actual percentages to the expected percentages. 3. The assumption for regression is that the residuals have a Normal Distribution. This means about 68% of the residuals would have a Z-score between -1 and 1, 95%% of the residuals would have a Z-score between -2 and 2 and all the residuals would have a Z-score between -3 and 3. The Column labeled "Standardized Residual" is the Z-score for each residual. Check to see what percentage of the data has 2-scores in each of these three intervals and compare the actual percentages to the expected percentages (68%, 95%, 100)Regression Analysis: BAC versus Beers The regression aquation is BAG - - 0. 0127 + 0.0180 Beers Predictor Coat BE COME Constant -0. 01270 0. 012 64 -1 - 00 0 - 332 0. 017964 0. 002402 7. 48 0-000 - 0.0204410 A-9q Analysis of Variance douECS HB P S Regression 1 0. 023375 0. 023375 55-94 0.000 Residual Error 14 G. 005850 0.060418 Total 0. 029225 Obs Beers FLE BE Fit Residual St Reaid 5.90 D . 10060 D, 07712 0, 00513 1: 16 2.00 D. 03060 0.02323 0.36 9.00 D. 19000 0. 14807 0. 04103 2. 410 0. 12000 0, 13101 0. 00920 -0.01101 3.00 0. 04060 0. 04119 0. 00671 -0.00110 -0. 06 7.GD D. 11305 0. 00733 -0. 1805 -0. 95 0. GOOD 0,04119 0.00671 D. 62801 5.60 D. OT712 0,06513 -0. 01712 -D . BT 3.00 0. 02060 0,04119 0, 0671 -0, 02119 -1: 10 0. 05060 0, 07712 0.00513 -0. 02712 -1. 37 1 1 4.00 0.07060 0.05915 0. 09547 0. 01085 0.65 12 6.00 0. 10090 0. 904 02 0.25 13 5.00 0.08560 10, 07712 0, 00513 0. 40 14 D. 11305 0,09753 -0, 02305 1.21 15 1:00 0. 01060 0.00526 0. 01049 D. 60474 0. 27 4.90 0.08090 0.08915 0.09547 -0.90915 At danoben an observation with a large standardized residual. Predicted Values for New Observations New Com FLE BE FLE 954 FI 0.07743 D. 00513 [D . 06418, 0.08812) 40 . 03192, 0. 122321 D. 24657 0. 03683 (0. 26758, 0. 42657) 40. 20623, 0.436921 XX MX denotes a point that is an extreme outlier in the predictors. Values of Predictors For New Choservations Make Hidejum fo MC New Qos Beers 510 Histogram 29,0 -10.1 -012 -0.01 160