Hi, can someone help me with these questions?

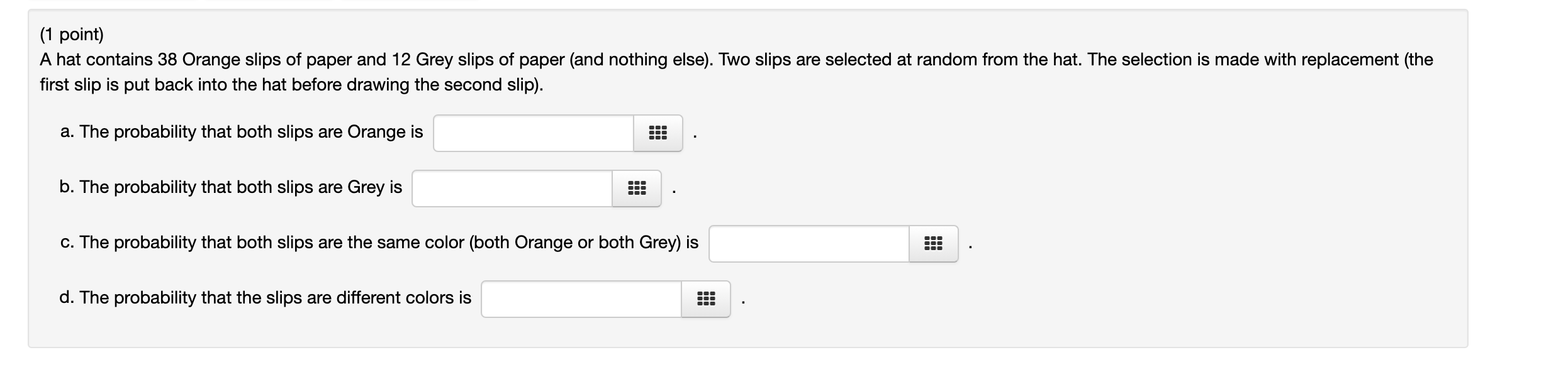
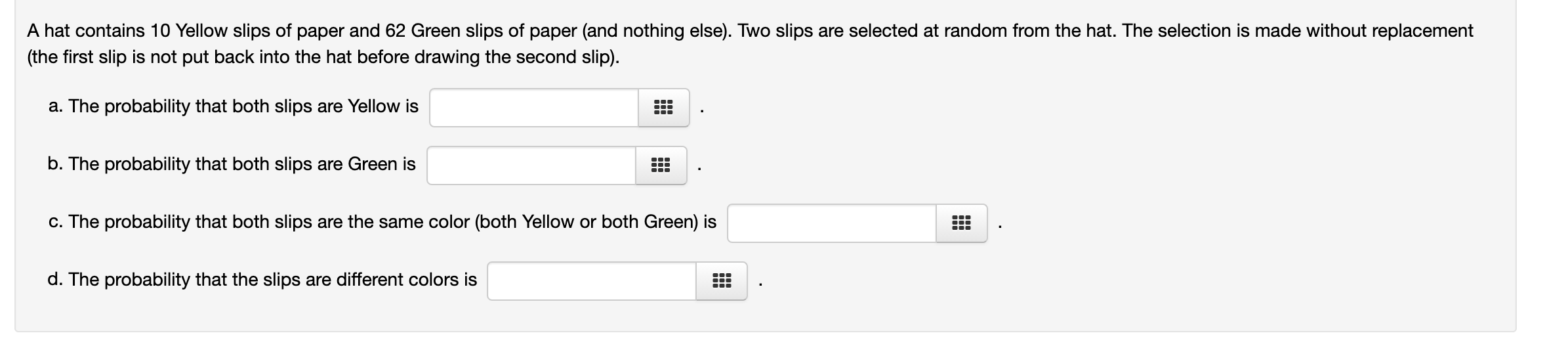
(1 point) a. If the knowledge that an event A has occurred changes the expected probability of a second event B, then the events A and B are said to be 0 A. mutually exclusive. 0 B. the sample space. 0 c. dependent. O D. independent. b. If the knowledge that an event A has occurred (on a particular observation) implies that a second event B cannot occur (on the same observation), then the events A and B are said to be 0A. the sample space. 0 B. independent. 0 G. mutually exclusive. 0 D. collectively exhaustive. c. If the knowledge that an event A has occurred does not change the expected probability of a second event B. then the events A and B are said to be 0A. the sample space. 0 B. independent. 0 C. mutually exclusive. 0 D. dependent. A jar contains 13 red balls, 22 green balls, and 35 yellow balls. A sequence of three balls is selected (with replacement) from the jar. a. The probability that the rst ball is green is l b. The probability that all three balls are green is l c. The probability that at least one of three balls is red or yellow . d. The probability that none of the balls are green is ' (1 point) A college mathematics course meets two days every week for one hour each day. The instructor chooses a random time during each class and counts the number of students present at that time. On any particular day, the probability that the instructor performs this count during the rst half of class is 0.71. a. On a particular day, what is the probability that the instructor performs the count during the second half of class? ' (do not convert to percent!) b. During a particular week, assume the counting time chosen on the second day of the week is independent of the counting time chosen on the first day. What is the probability thatrthe count is performed during the rst half of class on both days of that week? (do not convert to percent!) c. During a particular week, assume the counting time chosen on the second day of the week is independent of the counting time chosen on the first day. What is the probability that the count is performed during the second half of class on both days of that week? (do not convert to percentl) (1 point) A statistics class consists of 27 female students and 14 male students. Two different students are selected at random. a. The conditional probability that the second student is Male, given that the first student is Female, is b. The conditional probability that the second student is Female, given that the rst student is Male, is (1 point) A statistics class consists of 31 female students and 14 male students. Two different students are selected at random. a. The conditional probability that the second student is Female, given that the first student is Female, is b. The conditional probability that the second student is Male, given that the first student is Male, is "' An hat contains 199 slips of paper. 39 of these are Blue; the rest are Pink. Two slips are selected at random from the hat. ' With replacement (a) If the selection is made with replacement (the first slip is put back into the hat before drawing the second slip), the probability that both slips are Blue is Suppose that a single die with 10 sides (numbered 1, 2, 3, ... , 10) is rolled twice. Compute the probability of each of the following events. The first roll is even: The second roll is even: Both rolls are even:(1 point) In a survey of one-hundred people, the following data were obtained regarding gender and educational background. Female Male Total College degree 31 28 59 Nocollegedegree 20 21 41 Total 51 49 100 If a person is selected at random from those surveyed, find the probability of each of the following events. a. The person is female or has a college degree. 7 V l Answer: a: b. The person is male or does not have a college degree. Answer: 55E 0. The person is female or does not have a college degree. Answer: H: . (1 point) An insurace company has data on 222 motor vehicle accidents involving its policyholders. Each accident is classified according to whether there were any injuries or fatalities, and whether the at-fault driver was using some kind of distracting device (for example, texting while driving, which is now illegal in Georgia). The data are summarized in the table below. Device No Device TOTAL No injuries or fatalities 57 75 132 No fatalities, but at least one injury 21 39 60 At least one fatality 14 16 30 TOTAL 92 130 222 An insurance agent randomly selects one of these 222 accidents to review. Compute the following probabilities: a. The selected accident had no injuries or fatalities. b. In the selected accident, the at-fault driver was using some kind of distracting device. c. The selected accident had no injuries/fatalities, and the at-fault driver was not using a distracting device. d. The selected accident had no injuries/fatalities, or the at-fault driver was not using a distracting device. e. The selected accident had at least one fatality, and the at-fault driver was using a distracting device.(1 point) A hat contains 38 Orange slips of paper and 12 Grey slips of paper (and nothing else). Two slips are selected at random from the hat. The selection is made with replacement (the first slip is put back into the hat before drawing the second slip). a. The probability that both slips are Orange is 55E b. The probability that both slips are Grey is d. The probability that the slips are different colors is l A hat contains 10 Yellow slips of paper and 62 Green slips of paper (and nothing else). Two slips are selected at random from the hat. The selection is made without replacement (the first slip is not put back into the hat before drawing the second slip). a. The probability that both slips are Yellow is b. The probability that both slips are Green is =:: d. The probability that the slips are different colors is