Hi, can someone help me with these questions?

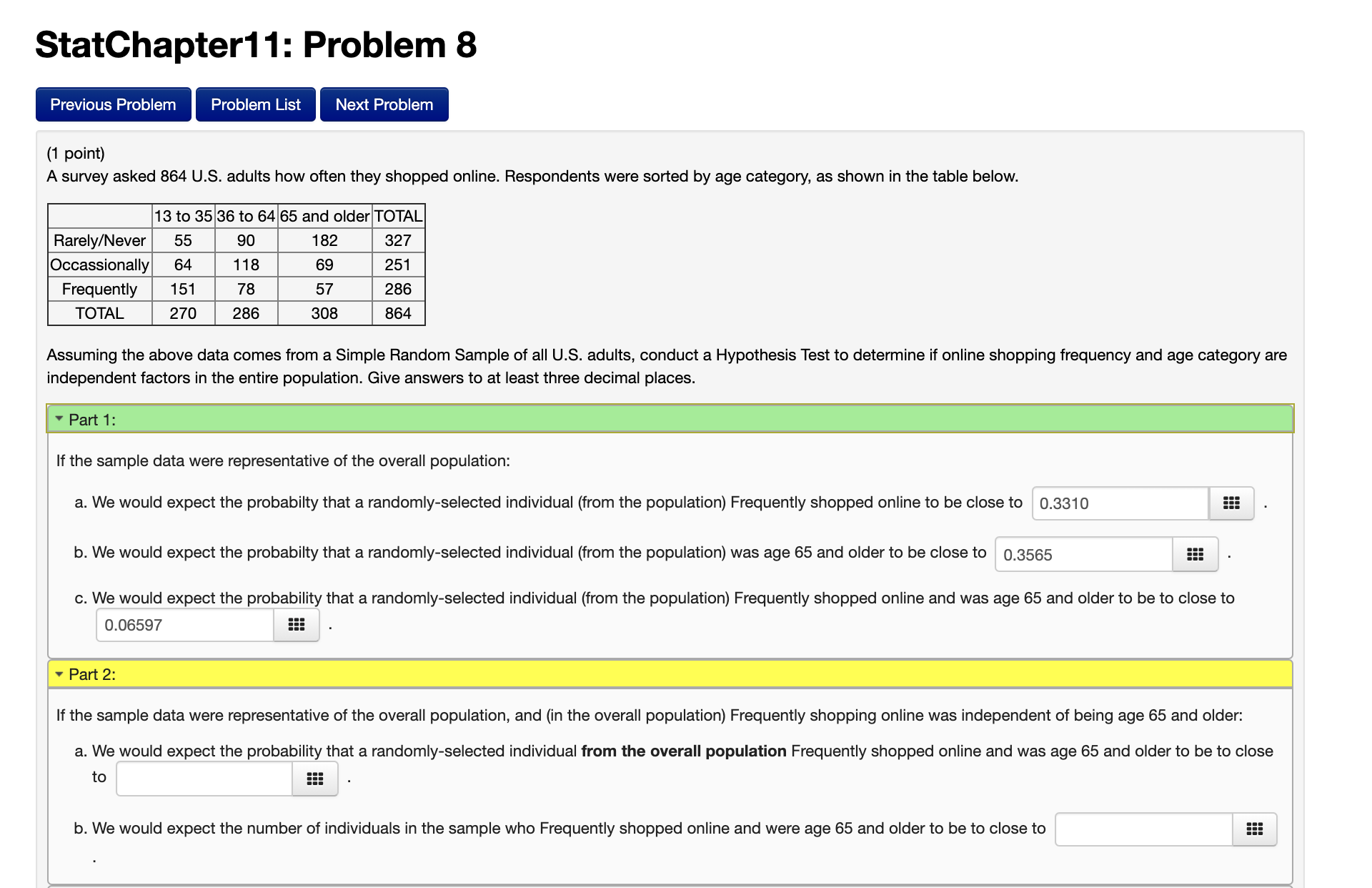
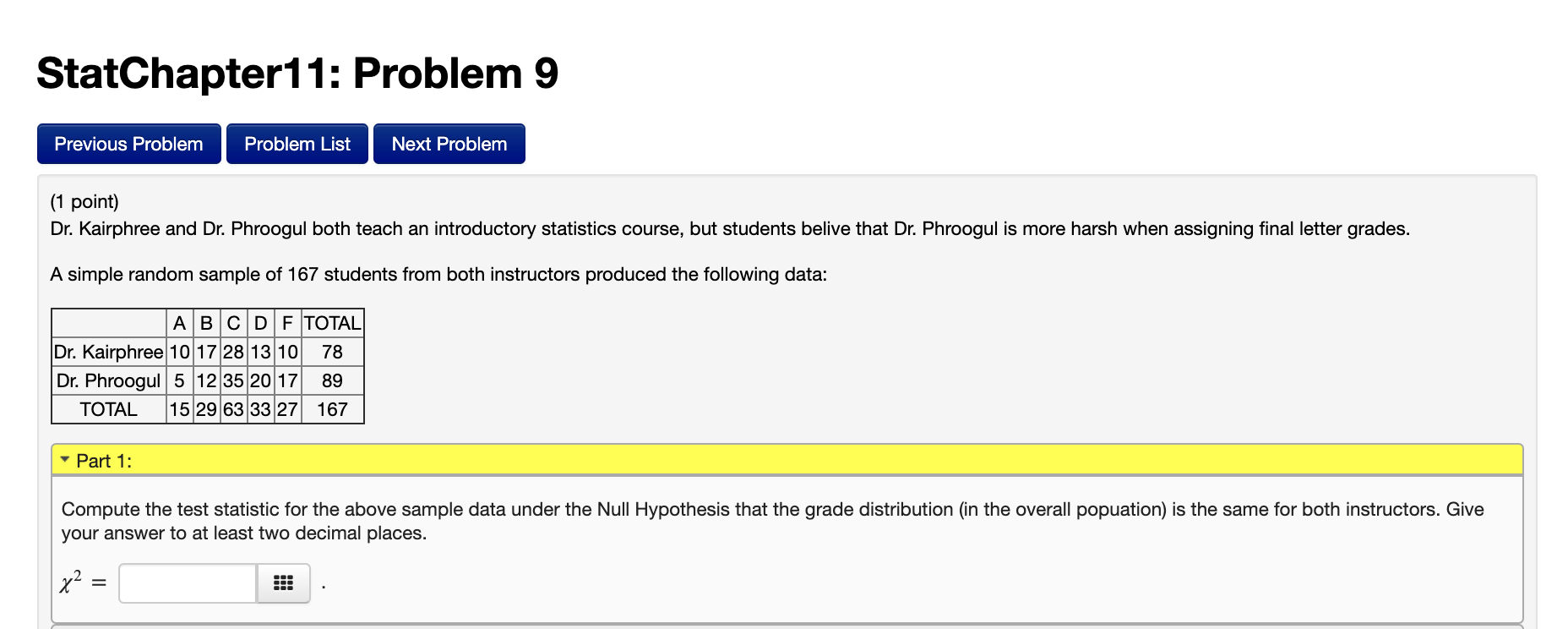
StatChapter11: Problem 6 (1 point) Is mobile device ownership affected by the type of community in which people live? A survey of 758 people produced the counts shown in the table below (for the purpose of this survey, "cellphone" means a mobile device that is not a smartphone). SU b urban No Mobile 39 74 132 245 Cellphone 53 93 4B 1 94 Smartphone 168 87 64 319 TOTAL 260 254 244 758 Assuming the above data comes from a Simple Random Sample, conduct a Hypothesis Test to determine if there is an association between device ownership and type of community in the entire population. ' Part 1: If the sample data were representative of the overall population: a. We would expect the probabilty that a randomly-selected individual (from the population) owns Cellphone be close to 0.2559 b. We would expect the probabilty that a randomly-selected individual (from the population) lived in a(n) Urban community to be close to 0.3430 c. We would expect the probability that a randomly-selected individual (from the population) owns a Cellphone and lives in a(n) Urban community to be to close to If the sample data were representative of the overall population, and (in the overall population) owning a Cellphone was independent of living in a(n) Urban community: a. We would expect the probability that a randomly-selected individual (in the overall population) owns a Cellphone and lives in a(n) Urban community to be to close to 0.0878 ::= b. We would expect the number of individuals in the sample who own a Cellphone and live in a(n) Urban community to be to close to 66.54 Compute the test statistic for the above sample data under the Null Hypothesis that type of mobile device and type of community are independent factors. Give your answer to at least two decimal places. 32 = as StatChapter11: Problem 8 (1 point) A survey asked 864 U.S. adults how often they shopped online. Respondents were sorted by age category, as shown in the table below. 13 to 35 36 to 64 65 and older TOTAL Flare ly/Never 55 90 1 82 327 Occassionally 64 1 18 Frequently 1 51 78 TOTAL 270 286 Assuming the above data comes from a Simple Random Sample of all U.S. adults, conduct a Hypothesis Test to determine if online shopping frequency and age category are independent factors in the entire population. Give answers to at least three decimal places. If the sample data were representative of the overall population: a. We would expect the probabilty that a randomly-selected individual (from the population) Frequently shopped online to be close to 0.3310 b. We would expect the probabilty that a randomly-selected individual (from the population) was age 65 and older to be close to Q3555 c. We would expect the probability that a randomly-selected individual (from the population) Frequently shopped online and was age 65 and older to be to close to 0.06597 iii ' Part 2: If the sample data were representative of the overall population, and n the overall population) Frequently shopping online was independent of being age 65 and older: a. We would expect the probability that a randomly-selected individual from the overall population Frequently shopped online and was age 65 and older to be to close to b. We would expect the number of individuals in the sample who Frequently shopped online and were age 65 and older to be to close to StatChapter11: Problem 9 Previous Problem Problem List Next Problem (1 point) Dr. Kairphree and Dr. Phroogul both teach an introductory statistics course, but students belive that Dr. Phroogul is more harsh when assigning final letter grades. A simple random sample of 167 students from both instructors produced the following data: ABCD F TOTAL Dr. Kairphree 10 17 28 13 10| 78 Dr. Phroogul 5 12 35 20 17 89 TOTAL 15 29 63 33 27 167 Part 1: Compute the test statistic for the above sample data under the Null Hypothesis that the grade distribution (in the overall popuation) is the same for both instructors. Give your answer to at least two decimal places. x2 =