Hi dears,

I need your support to solve this case using linear programming using EXCEL solver & writing the objective and constraints.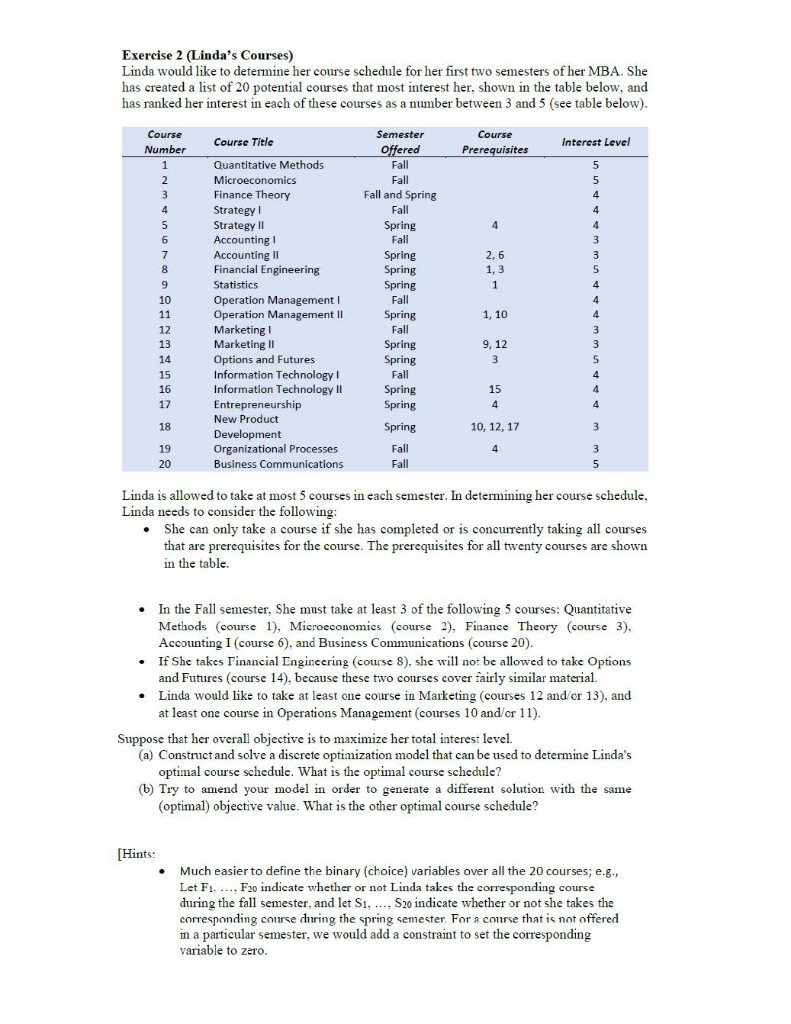

Exercise 2 (Linda's Courses) Linda would like to determine her course schedule for her first two semesters fher MBA. She has created a list of 20 potential courses that most interest her, shown in the table below, and has ranked her interest in each of these courses as number between 3 and 5 (see table below). Course Semester Course Interest Level Course Title Number Offered Fall Prerequisites Quantitative Methods Microeconomics 1 5 Fall 2 5 Fall and Spring Finance Theory 4 Fall Strategy 4 trategy Fall Ac 2, 6 7 Accounting I Financial Engineering Spring Spring Spring 1, 3 A Statistics 1 Fall 4 10 Operation Management I Operation Management I Marketing I Marketing I 11 Spring Fall 1, 10 4 12 3 13 Spring Spring 9, 12 Options and Futures Information Technology I Information Technology I Entrepreneurship New Product 14 Fall 15 4 16 Spring Spring 15 17 4 18 Spring 10, 12, 17 3. Development 19 Processes Fall ogzaoar Business Communications 20 Fall 5 Linda is allowed to take at most 5 courses in each semester. In determining her course schedule, Linda needs to consider the following: She can only take a course if she has completed or is concurently taking all courses that are prerequisites for the course. The prerequisites for all twenty courses are shown in the table In the Fall semester, She must take at least 3 of the following 5 courses: Quantitative Methods (course 1), Mieroeconomics (course 2), Finance Theory (course 3), Accounting I (course 6), and Business Communications (course 20). f She takes Financial Engineering (course 8), she will not be allowed to take Options and Futures (course 14), because these two courses cover fairly similar material Linda would like to take at least one course in Marketing (courses 12 and/or 13), and t least one course in Operations Management (courses 10 and/or 11). Suppose that her overall objective is to maximize her total interest level (a) Construct and solve a discrete optimization model that can be used to determine Linda's optimal course schedule. What is the optimal course schedule? (b) Try to amend your model in order to generate a different solution with the same (optimal) objective value. What is the other optimal course schedule? Hints: Much easier to define the binary (choice) variables over all the 20 courses; e.g., Let Fi. . F20 indicate whether or not Linda takes the corresponding course during the fall semester, and let S1, . S20 indicate whether or not she takes the corresponding course during the spring semester. For a conrse that is not offered in a particular semester, we would add a constraint to set the corresponding variable to zero. Additional constraints would be: Fall semester maximum O o Fall semester minimum Spring semester maximum o Spring semester minimum o A constraint for each prerequisite A constraint for Financial Engineering or Options o A constraint for Marketing C ectar minimm. A constraint for Operations Management] Exercise 2 (Linda's Courses) Linda would like to determine her course schedule for her first two semesters fher MBA. She has created a list of 20 potential courses that most interest her, shown in the table below, and has ranked her interest in each of these courses as number between 3 and 5 (see table below). Course Semester Course Interest Level Course Title Number Offered Fall Prerequisites Quantitative Methods Microeconomics 1 5 Fall 2 5 Fall and Spring Finance Theory 4 Fall Strategy 4 trategy Fall Ac 2, 6 7 Accounting I Financial Engineering Spring Spring Spring 1, 3 A Statistics 1 Fall 4 10 Operation Management I Operation Management I Marketing I Marketing I 11 Spring Fall 1, 10 4 12 3 13 Spring Spring 9, 12 Options and Futures Information Technology I Information Technology I Entrepreneurship New Product 14 Fall 15 4 16 Spring Spring 15 17 4 18 Spring 10, 12, 17 3. Development 19 Processes Fall ogzaoar Business Communications 20 Fall 5 Linda is allowed to take at most 5 courses in each semester. In determining her course schedule, Linda needs to consider the following: She can only take a course if she has completed or is concurently taking all courses that are prerequisites for the course. The prerequisites for all twenty courses are shown in the table In the Fall semester, She must take at least 3 of the following 5 courses: Quantitative Methods (course 1), Mieroeconomics (course 2), Finance Theory (course 3), Accounting I (course 6), and Business Communications (course 20). f She takes Financial Engineering (course 8), she will not be allowed to take Options and Futures (course 14), because these two courses cover fairly similar material Linda would like to take at least one course in Marketing (courses 12 and/or 13), and t least one course in Operations Management (courses 10 and/or 11). Suppose that her overall objective is to maximize her total interest level (a) Construct and solve a discrete optimization model that can be used to determine Linda's optimal course schedule. What is the optimal course schedule? (b) Try to amend your model in order to generate a different solution with the same (optimal) objective value. What is the other optimal course schedule? Hints: Much easier to define the binary (choice) variables over all the 20 courses; e.g., Let Fi. . F20 indicate whether or not Linda takes the corresponding course during the fall semester, and let S1, . S20 indicate whether or not she takes the corresponding course during the spring semester. For a conrse that is not offered in a particular semester, we would add a constraint to set the corresponding variable to zero. Additional constraints would be: Fall semester maximum O o Fall semester minimum Spring semester maximum o Spring semester minimum o A constraint for each prerequisite A constraint for Financial Engineering or Options o A constraint for Marketing C ectar minimm. A constraint for Operations Management]