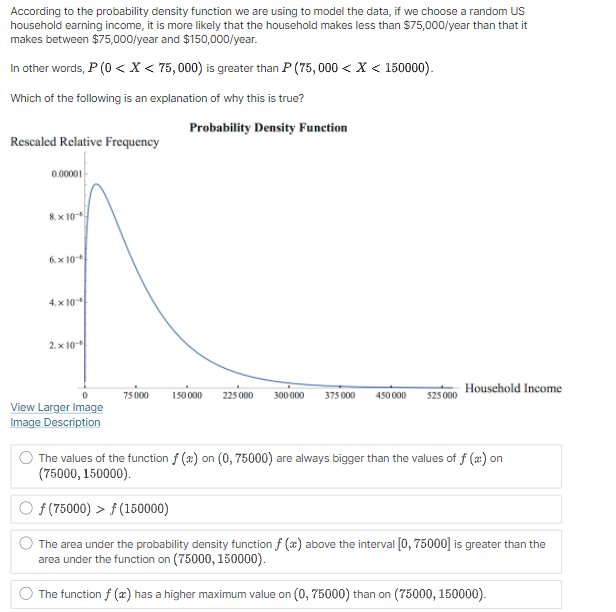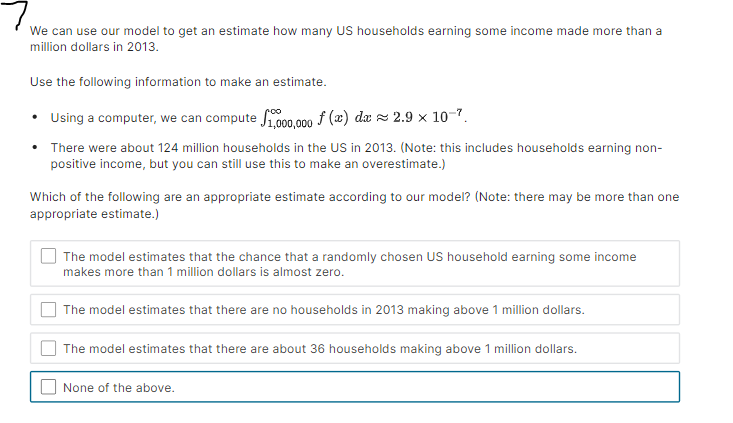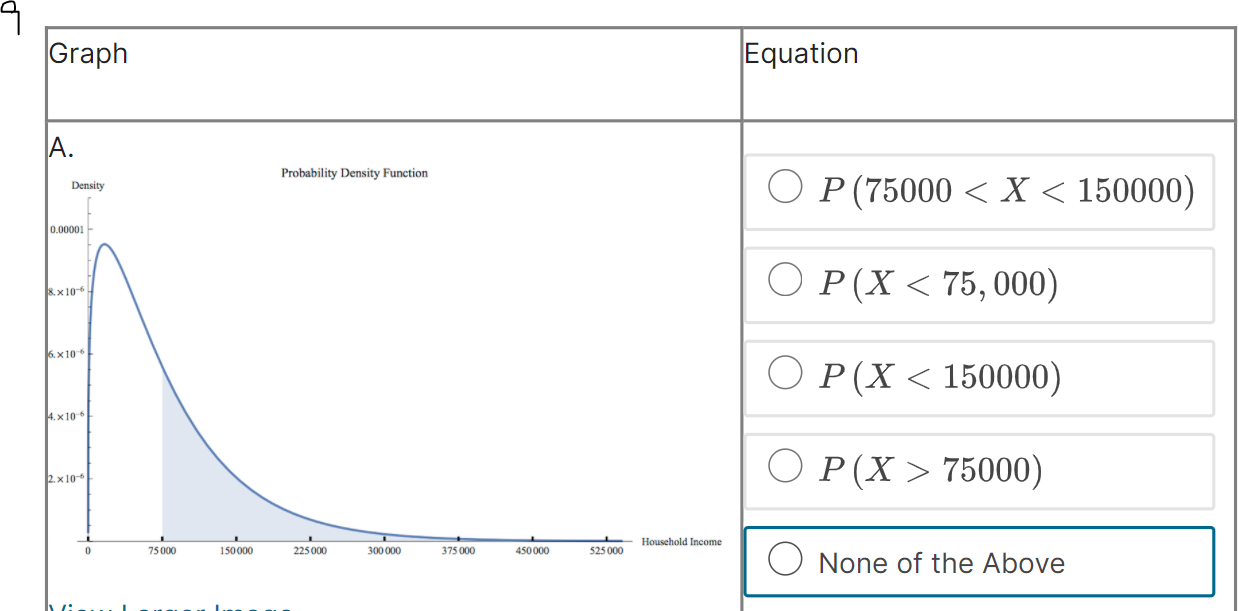
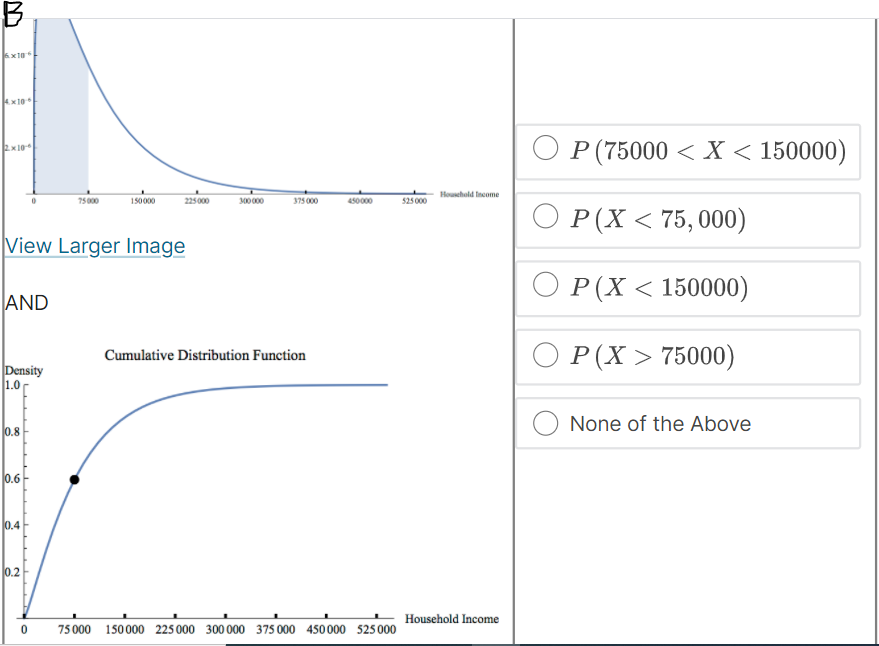
Hi expert only answer please no explanation required

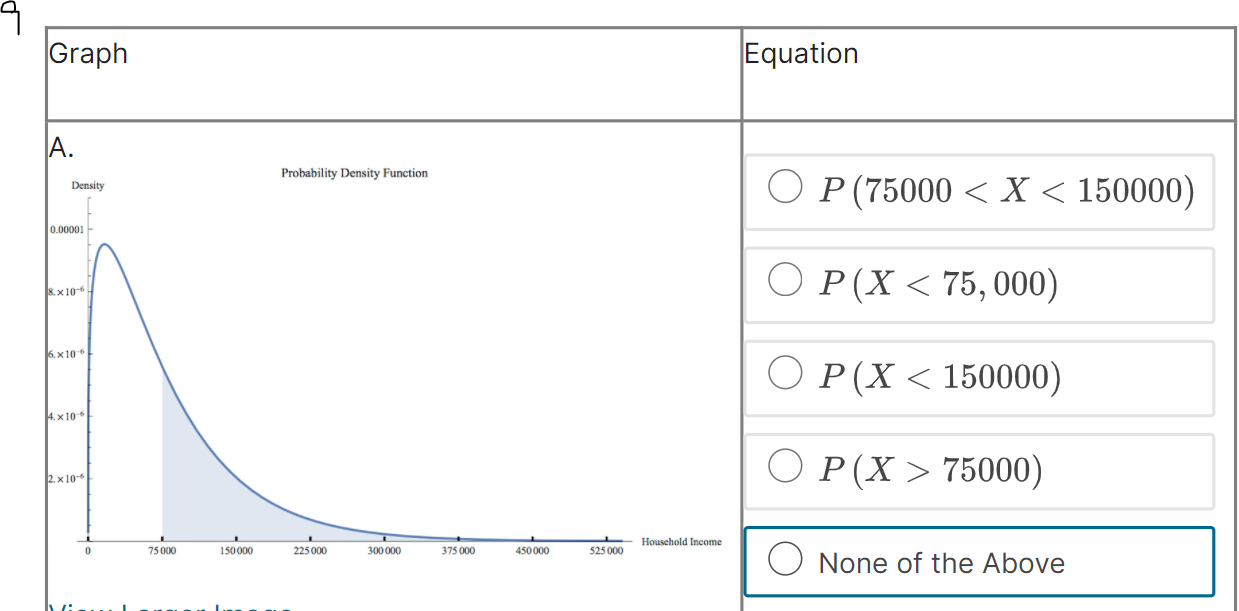
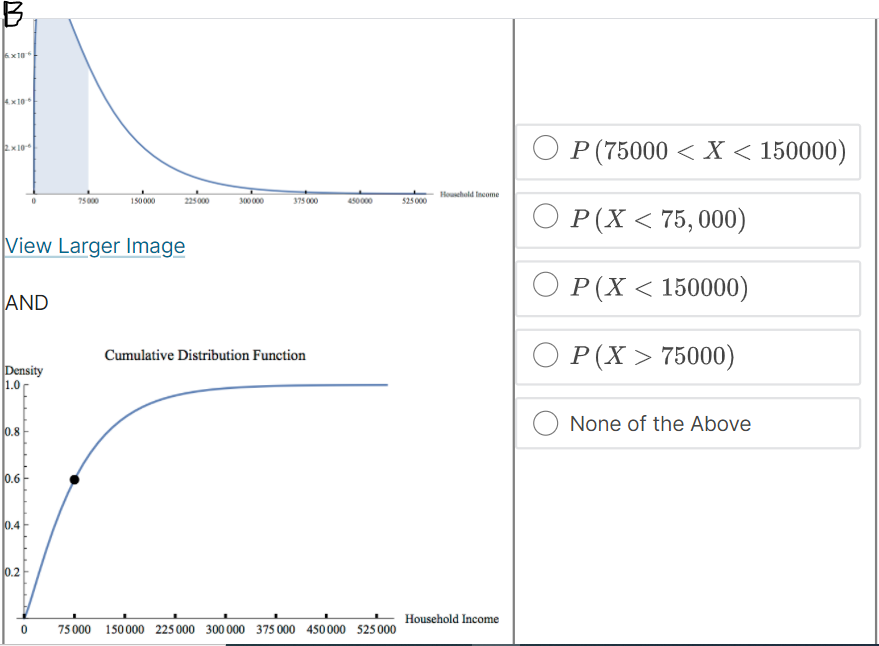
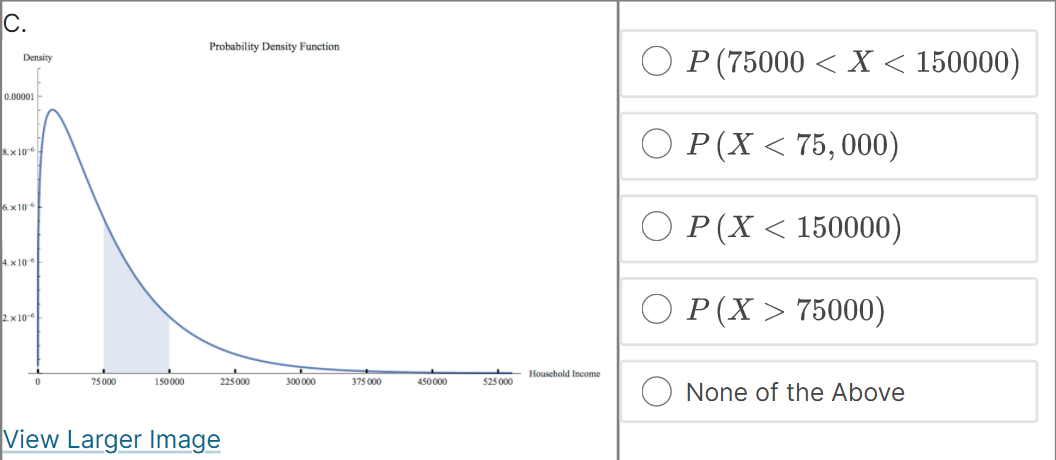
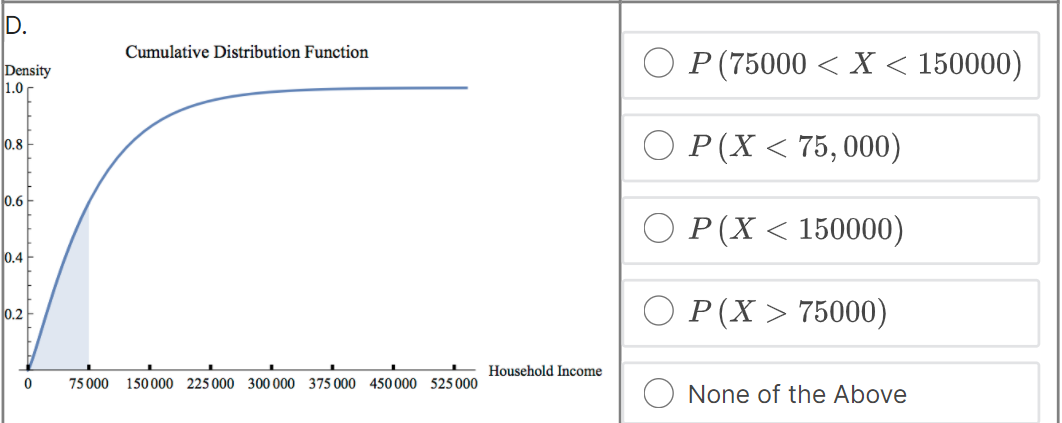
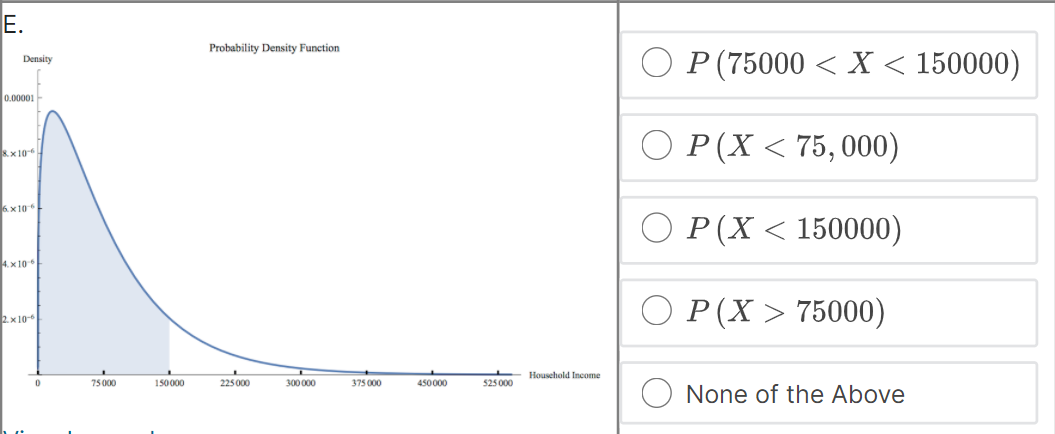
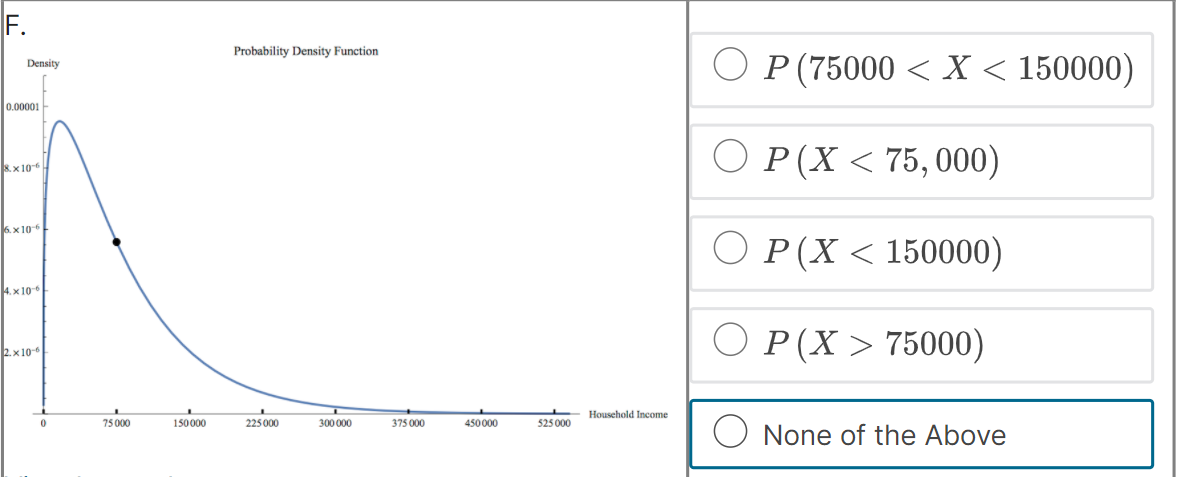
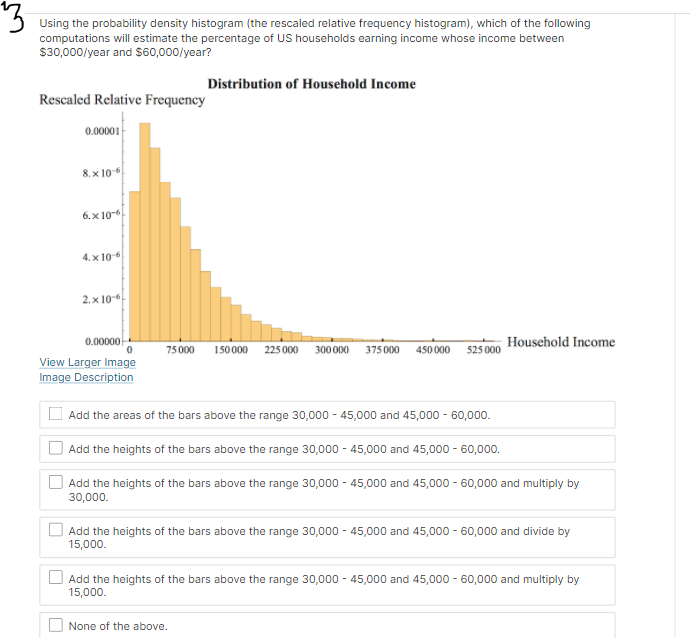
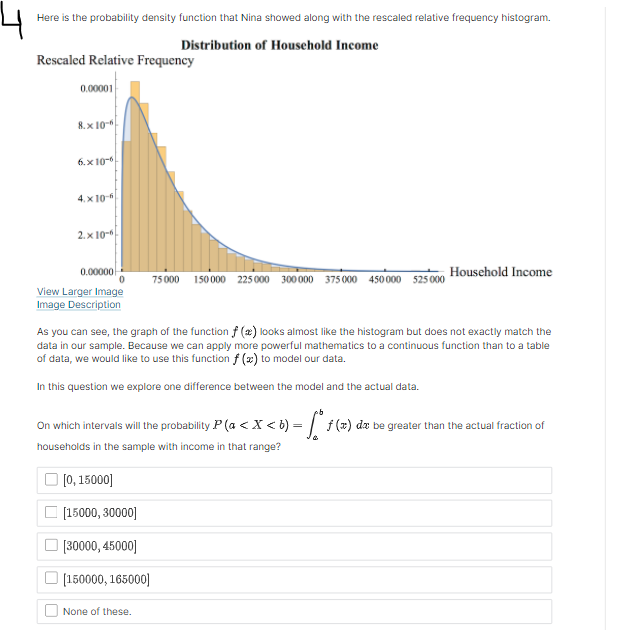
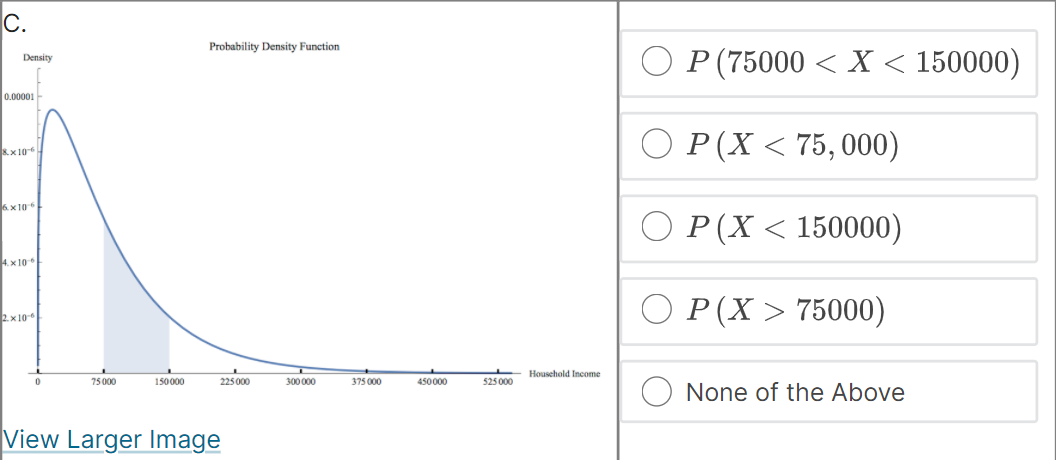
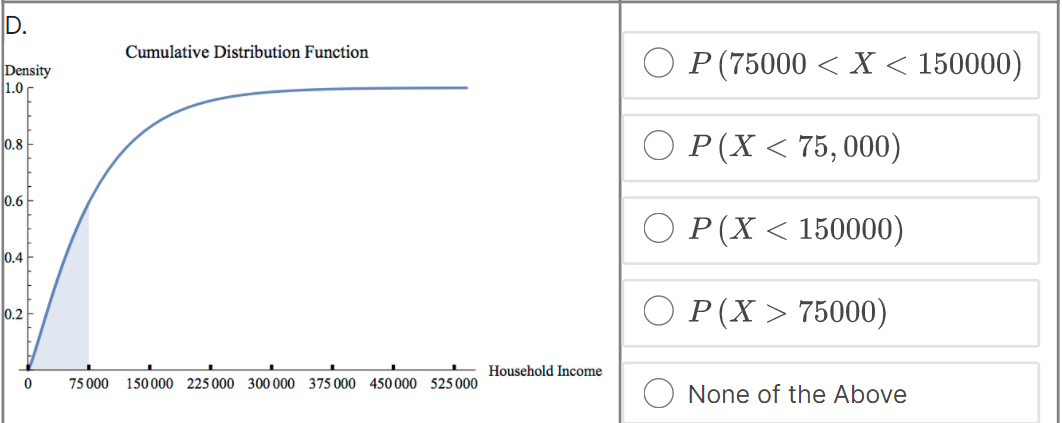
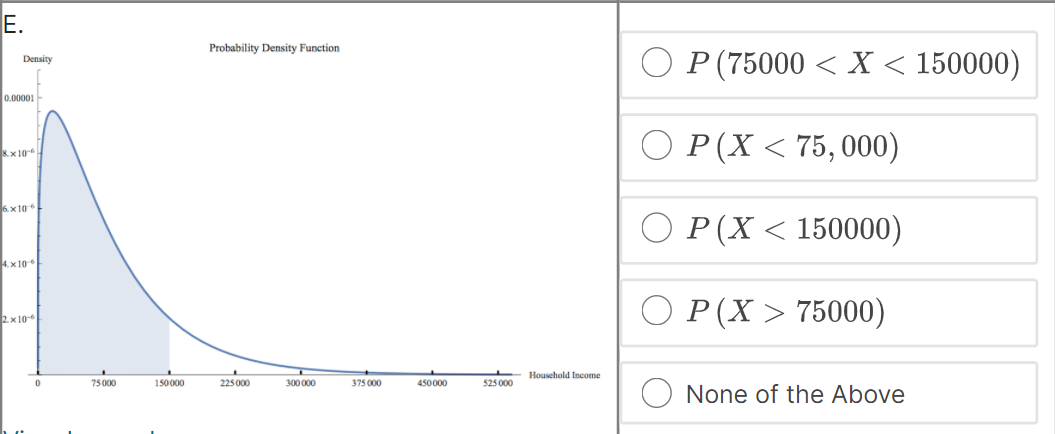
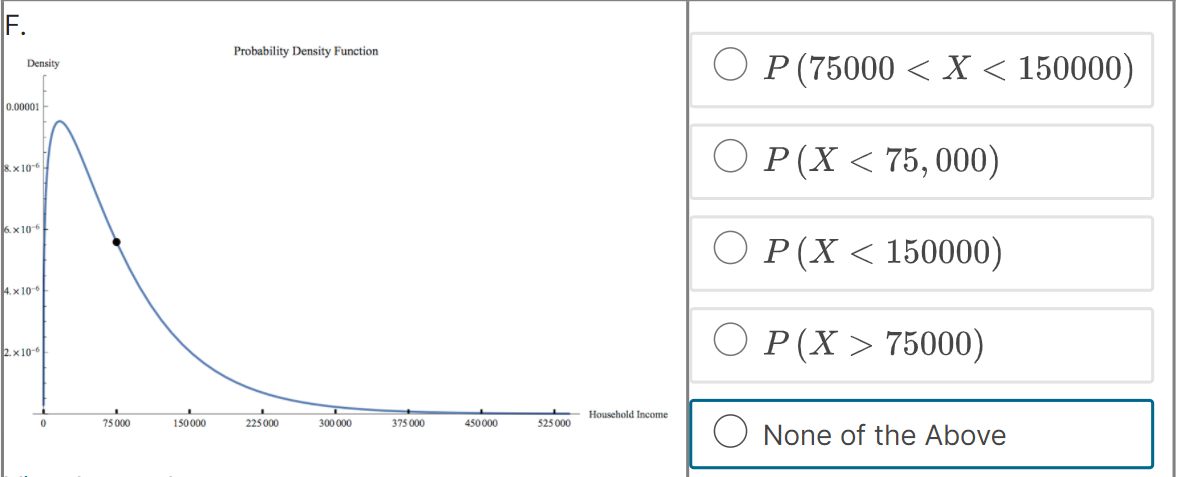
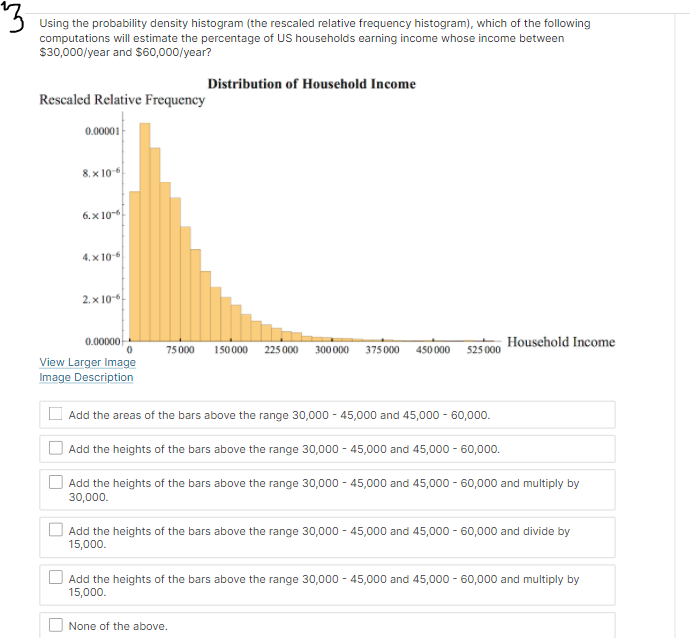
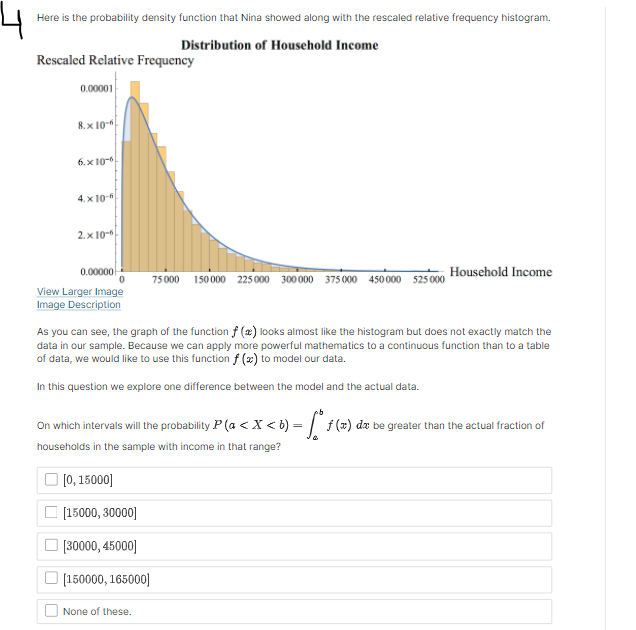
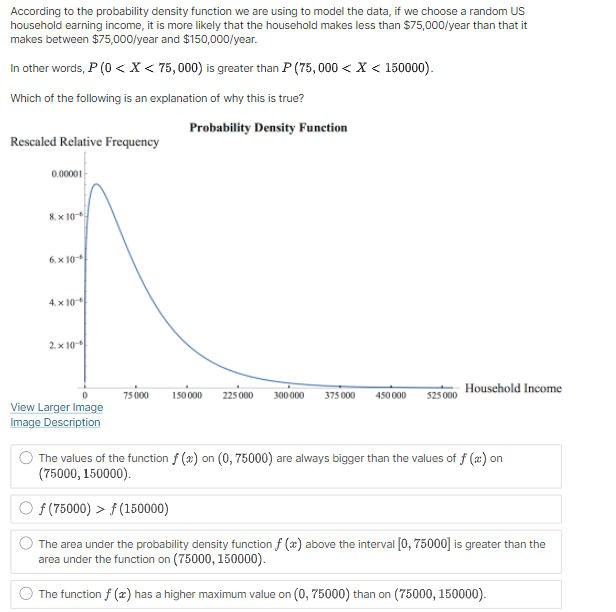
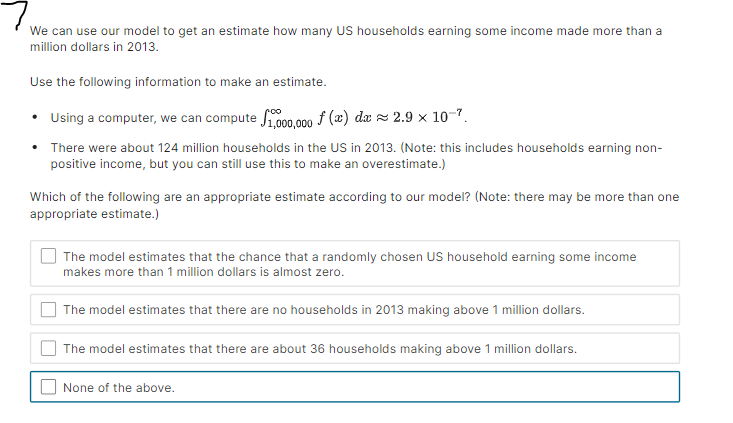
Suppose that f (@:) is the probability density function for the random variable X = household income in the US. Which integral measures P (14500 75000) Household Income 75 000 150 000 225 000 300 000 375 000 450 000 525 000 None of the Above4 x10 . O P (75000 75000) 1.0 0.8 None of the Above 0.6- 0.4- 0.2 0 75000 150 000 225000 300 000 375 000 450 000 525000 - Household IncomeC. Probability Density Function Density O P (75000 75000) Household Income 75 000 150 000 225 000 300 000 375 000 450 000 525 000 None of the Above View Larger ImageD. Cumulative Distribution Function Density O P (75000 75000) Household Income 0 75000 150 000 225000 300 000 375 000 450 000 525000 O None of the AboveE. Probability Density Function Density O P (75000 75000) Household Income 75 000 150 000 225 000 300 000 375 000 450 000 525 000 ONone of the AboveF. Probability Density Function Density O P (75000 75000) Household Income 75 000 150 000 225000 300 000 375 000 450 000 $25 000 O None of the AboveWhich integral measures the probability of a US household having income above $15,000/year? This is denoted as P (X > 15, 000). O f(x) da 15,000 O 1 - f(z) da 15,000 O 450,000 f (x) da 15,000 O f (x) da O None of these.3 Using the probability density histogram (the rescaled relative frequency histogram), which of the following computations will estimate the percentage of US households earning income whose income between $30,000/year and $60,000/year? Distribution of Household Income Rescaled Relative Frequency 0.00001 8. x 10-6 6. x 10-6 4. x 10-6 2. x 10-6 0.00000 0 75000 150 000 225 000 300 000 375000 450000 525000 Household Income View Larger Image Image Description Add the areas of the bars above the range 30,000 - 45,000 and 45,000 - 60,000. Add the heights of the bars above the range 30,000 - 45,000 and 45,000 - 60,000. Add the heights of the bars above the range 30,000 - 45,000 and 45,000 - 60,000 and multiply by 30,000. Add the heights of the bars above the range 30,000 - 45,000 and 45,000 - 60,000 and divide by 15,000. Add the heights of the bars above the range 30,000 - 45,000 and 45,000 - 60,000 and multiply by 15,000. None of the above.Here is the probability density function that Nina showed along with the rescaled relative frequency histogram. Distribution of Household Income Rescaled Relative Frequency 0.0000 1 8. x 10-6 6.x10-6 4. x 10 6 2. x 10-6 0.00000 75000 150 000 225000 300 000 375000 450000 525000 Household Income View Larger Image Image Description As you can see, the graph of the function f (@) looks almost like the histogram but does not exactly match the data in our sample. Because we can apply more powerful mathematics to a continuous function than to a table of data, we would like to use this function f (*) to model our data. In this question we explore one difference between the model and the actual data. Un which intervals will the probability P (a f (150000) The area under the probability density function f (@) above the interval [0, 75000] is greater than the area under the function on (75000, 150000). The function f (a) has a higher maximum value on (0, 75000) than on (75000, 150000).E. Which of the following are valid ways to compute the probability that a randomly chosen household income .X is greater than {1. dollars? El Compute f{o.], where fis the probability density function for X. m Compute In\" f) tit, where f is the probability density function for X. El Compute If f [t] dt, where f is the probability density function for X. El Compute 1 FM], whereF is the cumulative distribution function for X. : We can use our model to get an estimate how many US households earning some income made more than a million dollars in 2013. Use the following information to make an estimate. 0 Using a computer, we can compute Ransom ffm] rim 9:: 2.9 X 107. - There were about \"124 million households in the US in 2013. (Note: this includes households earning non positive income, but 1,rou can still use this to make an overestimate.) Which of the following are an appropriate estimate according to our model? [Note: there may be more than one appropriate estimate] D The model estimates that the chance that a randomly chosen US household earning some income makes more than 1 million dollars is almost zero. D The model estimates that there are no households in 213 making above1 million dollars. E] The model estimates that there are about 36 households making above'l million dollars. [I None of the above. The median of a set of data outs the data in half, separating the higher half of the data from the lower half. We define median for a continuous model similarly. The median of a continuous distribution is the value such that such that a randomly chosen 3: has a seat. chance of being higher than that value and a 50% chance of being lower. Which of the following do you think would compute the median, m, of the orobaoity density function f {at} ? {We'll come baolt to this question in the next 1.iideo.]l O Computem = \"0'5 ffm] do: 0 Find the ualuem such that 1:1 f (3:) do; = [L5 0 Find the ualuem such that I: f [m] dd: = 5U O None of the above. For each mathematical expression, find the image or images that visually represent the value of the expression. l[Every expression has at least one image. One has two images.) NOTE: The graphs are of probability density functions. The vertical axis represents the rescaled relative frequency, also called density