Hi! I don't know how to solve problems that have star signs on the number of the questions. Please help me solve the questions step by step. Thank you so much!

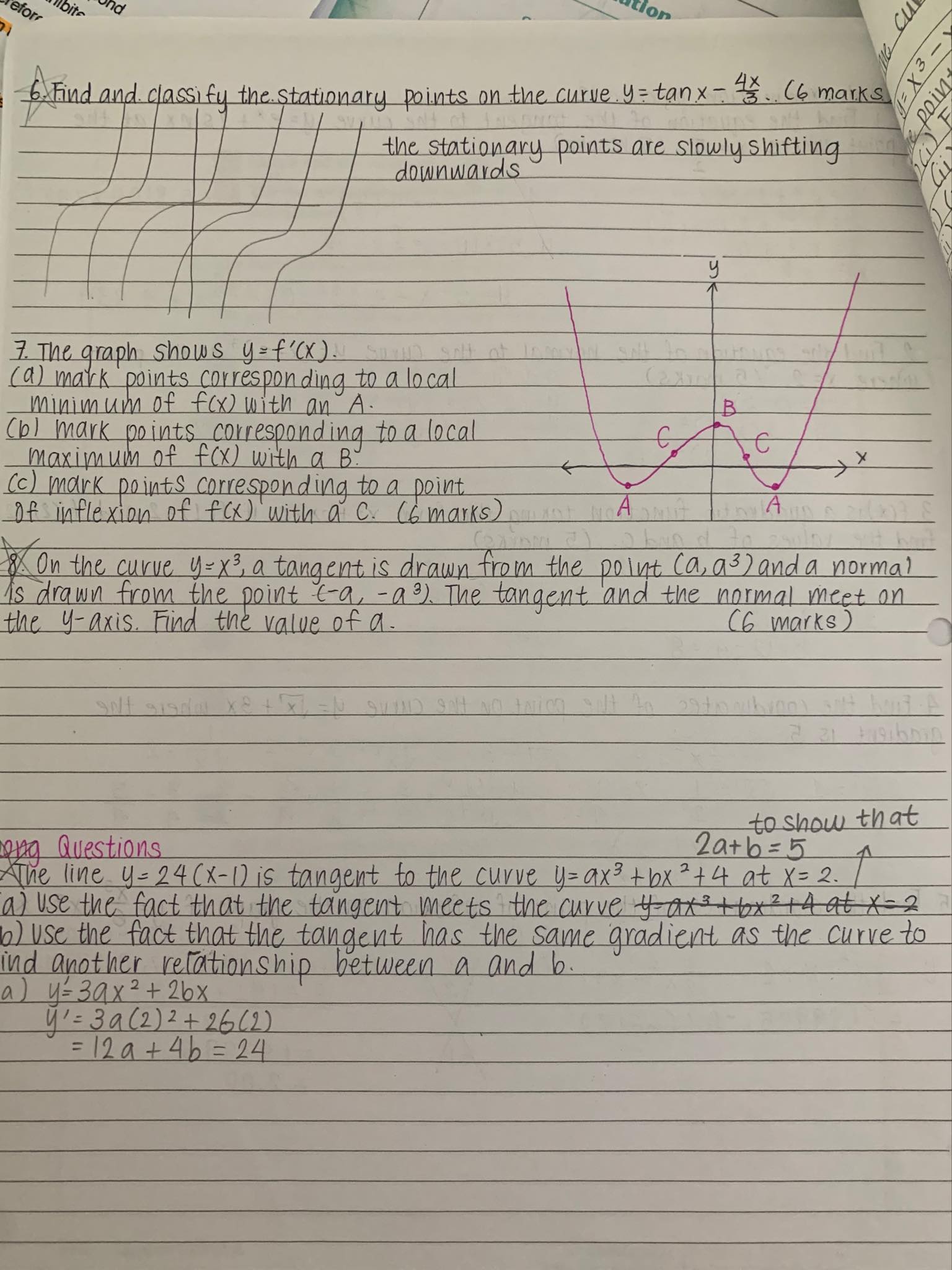
Find the equation of the normal to the curve y= ( x - 2 ) at the point where X = 2 . ( 5 marks ) 4 = ( x- 2) 3 undefined ? nols or Di 4 1 3 ( x - 2) 2 , 4= (2-2)3 =0 A NONtix = 3 ( 2 - 2 ) 2 = 0 1 0 . . y - 0 = 0+2 4=2 Xefor Ion cu 6 . Find and classify the stationary points on the curve . y = tanx - 3 . ( 6 marks. EX 3 pain the stationary points are slowly shifting downwards y 7 . The graph shows y = f' (x ) . ( a ) mark points corresponding to a local minimum of f(x) with an A . ( bl mark points corresponding to a local B maximum of f ( x ) with a B. C ( c ) mark points corresponding to a point of inflexion of f ( x ) with a C . ( 6 marks ) 8On the curve y= x3, a tangent is drawn from the point ( a, a3 ) and a normal is drawn from the point (- a, - a 3 ) . The tangent and the normal meet on the y- axis. Find the value of a . ( 6 marks ) to show that ong Questions 2 atb = 5 The line y = 24 ( x - 1) is tangent to the curve y= ax3 + bx 2 + 4 at X = 2. a ) use the fact that the tangent meets the curve tax + box ? +4 at x- 2 6 ) use the fact that the tangent has the same gradient as the curve to ind another relationship between a and b. a ) 4 = 30 x 2 + 26x 41= 39 ( 2 ) 2 + 26 ( 2) = 12 a + 46 = 24. ) The curve shown is part of the graph of. ( 10 marks ) y = x3 - X 2 - X+ 3 The point A is a local maximum and the point B is a point of inflexion 9 ) ( i ) Find the coordinates of A (i ) Find the coordinates of B 1) ( - 0. 33, 3. 19) 1 ) ( 1 , 2 ) A ) ( i ) Find the equation of the line containing B both A and B ( ij ) Find the equation of a tangent to the curve which is parallel to this line i) ( - 0 . 3 3 , 3 . 19 ) ( 1 , 2 ) MA = 1 2 - YI m = 2 - 3 . 19 = - 1.19 X2 - XI 1+ 0-33 1.33 = - 0 . 89 4 7 3 6 8421 4 = - 0 895 x + 3 IM . = - 0 . 8 9 4 7 3 6 8 421 4 - y, = m ( x - X 1 ) 3 . The population P of bacteria in thousands at a time t in hours e is modelled by P = 10+et - 3t. +20 ( a ) ( i ) Find the initial population of bacteria ( 1 2 marks ) P = 10+ 2 - 3(0 ) = 11 - (il ) At what time does the number of bacteria reach 14 million ? 14 . 0 0,0 0 0 1400 = 10+et- 3t 140 0 - 10 = et - 3t X = 7. 245467 X = 7. 25 hours ( b ) ( i ) Find dP 1390 = et - 3t P = 10+et - 3t dt . P' = et - 3 Find the time at which the bacteria are growing at a rate of 6 million per hour A ( c ) ( i ) Find dap and explain the physical significance of this quanti at 2 P" = et