Hi! I need help modifying the below code to compute the matrix determinant for this given matrix:

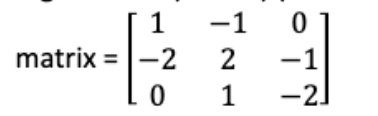
CODE FOR GAUSSIAN ELIMINATION PYTHON (PLEASE EDIT AS NEEDED TO COMPUTE THE MATRIX DETERMINANT):

import numpy as np

# Define the matrix A and vector b A = np.array([[1, 0, 2], [2, -1, 3], [4, 1, 8]], dtype=float) b = np.array([1, -1, 2], dtype=float)

# Combine matrix A and vector b into a single augmented matrix C C = np.column_stack((A, b))

# Initialize the success parameter E to 1 E = 1

# Get the size of the matrix n = C.shape[0]

# Iterate over each column j for j in range(n):

# Find the index of the row with the maximum absolute value in column j p = np.argmax(np.abs(C[j:, j])) + j

# If the maximum value is 0, set E to 0 and exit if C[p, j] == 0: E = 0 break

# If the pivot is not in the j-th row, swap the rows if p != j: C[[j, p], :] = C[[p, j], :]

# Eliminate the entries below the pivot in column j for i in range(j+1, n): C[i, :] -= (C[i, j]/C[j, j]) * C[j, :]

# Check if a unique solution was found if E == 1: # Initialize the solution vector x with zeros x = np.zeros(n)

# Back-substitution to solve for x for j in range(n-1, -1, -1): x[j] = (C[j, -1] - np.dot(C[j, j+1:n], x[j+1:n])) / C[j, j]

# Print the solution print("The solution is: ", x) else: print("The algorithm failed to find a unique solution.")

Please no copy and pasting from another answer and please provide code screenshots so I know your solution helps. Thank you! I will upvote if your solution helps me. :)

matrix =120121012