Hi, I would appreciate any help,

The % Mod Operator

This sort of "wrap-around" arithmetic is called modular arithmetic. We say "fifteen mod twelve" is equal to 3. (Just like how "15 o'clock" mod twelve would be "3 o'clock".) In Python, the mod operator is the % percent sign. Try typing the following into the interactive shell:

>>> 15 % 12

3

>>> 210 % 12

6

>>> 10 % 10

0

>>> 20 % 10

0

"Mod" is "Division Remainder"(Sort Of)

You can think of the mod operator as a "division remainder" operator. 21 5 = 4 remainder 1. And 21 % 5 = 1. This works pretty well for positive numbers, but not for negative numbers. -21 5 = -4 remainder -1. But the result of a mod operation will never be negative. Instead, think of that -1 remainder as being the same as 5 1, which comes to 4. This is exactly what -21 % 5 evaluates to:

>>> -21 % 5

4

But for the purposes of cryptography, we'll only be modding positive numbers.

Example using the Modulo Operator

One common use for the Modulo Operator is to find even or odd numbers. The code below uses the modulo operator to print all odd numbers between 0 and 10.

for number in range(1, 10):

if(number % 2 != 0)

print(number)

We can also create a small function to print out the full result of Euclidean division like so:

def euclidean_division(x, y):

 quotient = x // y 

remainder = x % y

 print(f"{quotient} remainder {remainder}") 

euclidean_division(10, 3) # 3 remainder 1

euclidean_division(11, 3) # 3 remainder 2

The // Integer Division Operator

You may have noticed the // operator used in the euclidean_division() function above. This is the integer division operator. It divides two numbers and rounds down. Try typing the following into the interactive shell:

>>> 41 // 7

5

>>> 41 / 7

5.857142857142857

>>> 10 // 5

2

>>> 10 / 5 

2.0

Notice that an expression with the // integer division operator always evaluates to an int, not a float.

Task1. Modular Exponentiation (power in modular arithmetic)

Given three numbers x, y and p, compute (x**y) % p.

Examples :

Input: x = 2, y = 5, p = 13

Output: 6

Explanation: 2**5 % 13 = 32 % 13 = 6.

Input: x = 7, y = 3, p = 11

Output: 2

Explanation: 7**3 % 11 = 343 % 11 = 2.

The problem with above solutions is, overflow may occur for large value of n or x. Therefore, power is generally evaluated under modulo of a large number.

Below is the fundamental modular property that is used for efficiently computing power under modular arithmetic.

(ab) % p = ( (a % p) (b % p) ) % p

For example a = 50, b = 100, p = 13

50 % 13 = 11

100 % 13 = 9

(50 * 100) % 13 = ( (50 % 13) * (100 mod 13) ) mod 13

or (5000) % 13 = ( 11 * 9 ) % 13

or 8 = 8

Algorithm:

int power(int x, int y, int p)

{

// Initialize result

int res = 1;

// Update x if it is more

// than or equal to p

x = x % p;

while (y > 0)

{

// If y is odd, multiply

// x with result

if((y & 1) == 1)

res = (res * x) % p;

// y must be even now

// y = y / 2

y = y >> 1;

x = (x * x) % p;

}

return res;

}

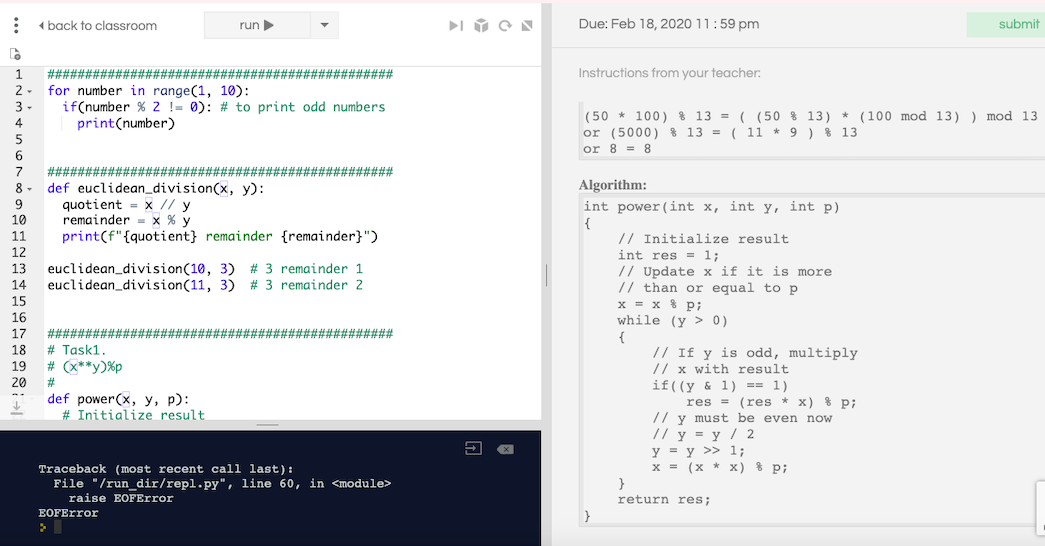
############################################## for number in range(1, 10): if(number % 2 != 0): # to print odd numbers print(number)

############################################## def euclidean_division(x, y): quotient = x // y remainder = x % y print(f"{quotient} remainder {remainder}")

euclidean_division(10, 3) # 3 remainder 1 euclidean_division(11, 3) # 3 remainder 2

This is the code I need help with..

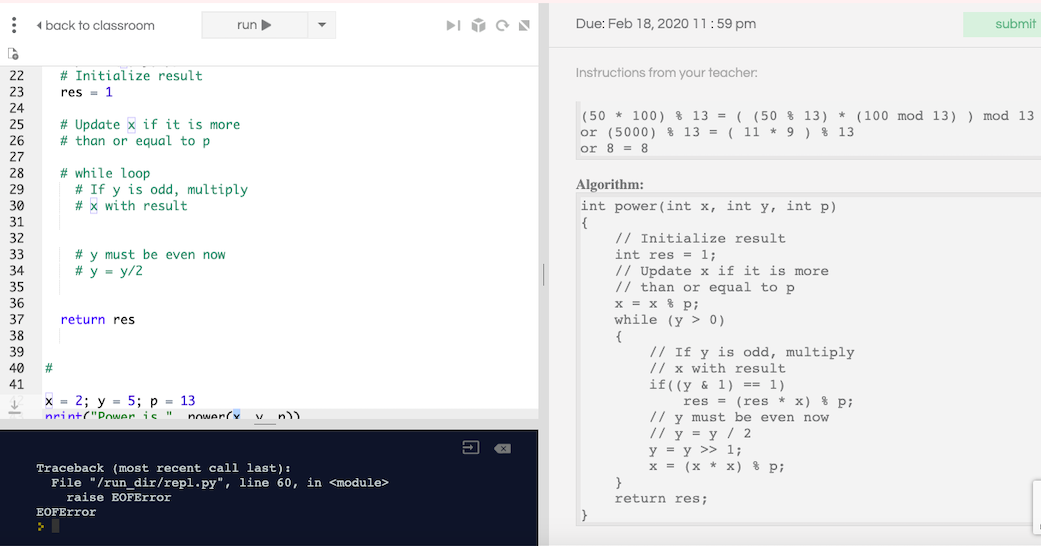
############################################## # Task1. # (x**y)%p # def power(x, y, p): # Initialize result res = 1

# Update x if it is more # than or equal to p

# while loop # If y is odd, multiply # x with result

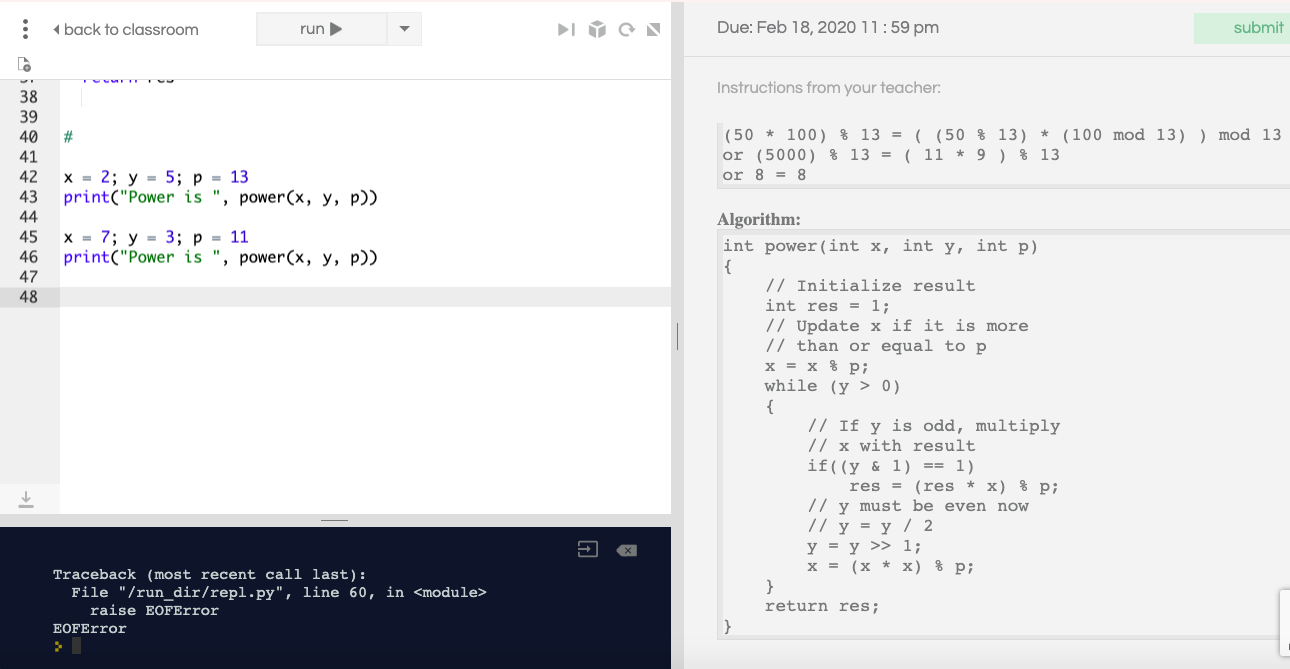
# y must be even now # y = y/2 return res # x = 2; y = 5; p = 13 print("Power is ", power(x, y, p))

x = 7; y = 3; p = 11 print("Power is ", power(x, y, p))

here what I need in the code

1. Appropriate algorithm

2. Code readability (proper indentation, appropriate variable names, etc)

back to classroom run - Due: Feb 18, 2020 11:59 pm submit Instructions from your teacher 3- ############################################## for number in range(1, 10): if(number % 2 != 0): # to print odd numbers print(number) + (50 * 100) % 13 = ( (50 % 13) * (100 mod 13) ) mod 13 or (5000) % 13 = ( 11 * 9 ) % 13 or 8 = 8 00 #################################### ###### def euclidean_division(x, y): quotient = X // y remainder - X % y print(f"{quotient} remainder {remainder}") Algorithm: int power (int x, int y, int p) 9 10 euclidean_division(10, 3) # 3 remainder 1 euclidean_division(11, 3) # 3 remainder 2 // Initialize result int res = 1; // Update x if it is more // than or equal to p X = X % P; while (y > 0) 18 19 20 # Task1. # x**y)%p # def power(x, y, p): # Initialize result // If y is odd, multiply // x with result if((y & 1) == 1) res = (res * x) % p; // y must be even now // y = y / 2 y = y >> 1; x = (x * x) % p; Traceback (most recent call last): File "/run_dir/repl.py", line 60, in raise EOFError EOFError return res; back to classroom run Due: Feb 18, 2020 11:59 pm submit Instructions from your teacher: # Initialize result res = 1 # Update x if it is more # than or equal to p (50 * 100) 8 13 = ( (50 % 13) * (100 mod 13) ) mod 13 or (5000) % 13 = ( 11 * 9 ) % 13 or 8 = 8 # while loop # If y is odd, multiply # X with result Algorithm: int power(int x, int y, int p) # y must be even now # y = y/2 // Initialize result int res = 1; // Update x if it is more // than or equal to p X = X % P; while (y > 0) return res X = 2; y = 5; p = 13 nrint("Power is " nowerly vn) // If y is odd, multiply // x with result if((y & 1) == 1) res = (res * x) % P; // y must be even now // y = y / 2 y = y >> 1; x = (x * x) & p; Traceback (most recent call last): File "/run_dir/repl.py", line 60, in raise EOFError EOFError return res; back to classroom run Due: Feb 18, 2020 11:59 pm submit Instructions from your teacher: (50 * 100) % 13 = ( (50 % 13) * (100 mod 13) ) mod 13 or (5000) % 13 = ( 11 * 9 ) % 13 or 8 = 8 X = 2; y = 5; p = 13 print("Power is ", power(x, y, p)) X = 7; y = 3; p = 11 print("Power is ", power(x, y, p)) Algorithm: int power(int x, int y, int p) // Initialize result int res = 1; // Update x if it is more // than or equal to p x = x % p; while (y > 0) // If y is odd, multiply 17 x with result if((y & 1) == 1) res = (res * x) % p; // y must be even now 17 y = y 1 2 y = y >> 1; x = (x * x) % p; Traceback (most recent call last): File "/run_dir/repl.py", line 60, in raise EOFError EOFError return res