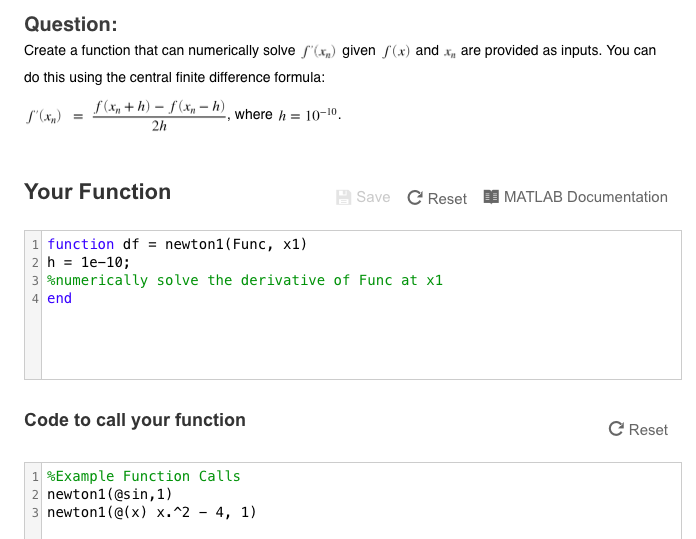
Hi, I'm currently really struggling on this question, it would be greatly appreciated (PLEASE COMPLETE USING MATLAB) Newtons Method approximates a root of a function by iterating through the equation where is the nth estimate for the root of the function f (x). In order to it- erate through this method, we need to provide an initial guess for the root, Ti For example, if we apply this method to f(a)sin(x) using x-1, we note that f'(a)cos(x) cos(1)--0.5574 sin(-0.5574) cos(-0.5574) 3-0.5574 - = 0.0659 cos(0.0659)-9.5722 x 10- We can see that as we iterate through Newtons Method we are converging towards 0, which is one of the roots of f(z) sin(r) Question: Create a function that can numerically solvef) given (x) and do this using the central finite difference formula: are provided as inputs. You can f (x" + h)-f(x" _ h), where h-10-10. 2h Your Function Save C Reset MATLAB Documentation 1 function df newton1 (Func, x1) 3%numerically solve the derivative of Func at x1 4 end Code to call your function C Reset %Example Function Calls 2 newton1(@sin,1) newton1(@(x) x."2 - 4, 1)