Question
Hi, I'm having problems solving this question in my STAT practical class. I need some helps and explanation about this. Consider a standard deck of
Hi, I'm having problems solving this question in my STAT practical class. I need some helps and explanation about this.
Consider a standard deck of 48 Japanese Hanafuda playing cards. The deck is divided into 12 suits, for each month of the year, with 4 cards per suit. In total there are 12 cards per season (3 months per season). The number of cards in the deck will be reduced via the following actions: Remove three of the four July (Winter-season) cards Remove four other cards that are not from the Winter-season months The cards that are removed are discarded, and so are not used for the remainder of this question. Therefore, now I have a modified deck consisting of 41 cards. Given this deck, consider the following scenario: Suppose that a card is randomly drawn from this reduced deck. Let W1 denote the event that this card is a Winter-season card. The drawn card (regardless of type) is then discarded. Suppose that a second card is randomly drawn from further reduced deck (now containing just 40 cards). let W2 denote the event that this card is a Winter-season card. Using this information, answer the following questions. (a) What is P(W1)? (b) What is
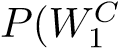
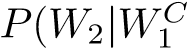
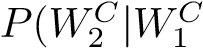
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


