Hi! I'm trying to solve the three-body problem using Euler method to solve differential equations in Python. This is the problem:

In physics and classical mechanics, the three-body problem is the problem of taking the initial positions and velocities (or momenta) of three point masses and solving for their subsequent motion according to Newton's laws of motion and Newton's law of universal gravitation. The three-body problem is a special case of the n-body problem. Unlike two-body problems, no general closed-form solution exists, as the resulting dynamical system is chaotic for most initial conditions, and numerical methods are generally required.

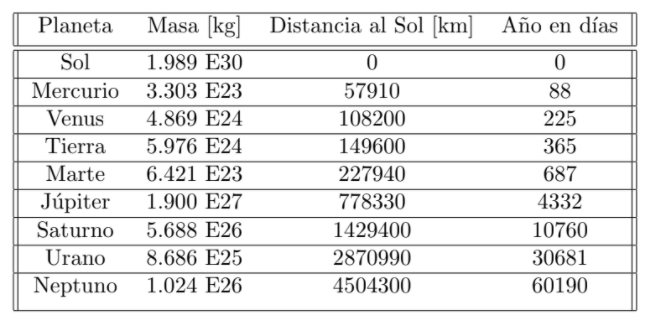
Given the data in the table, write a program that chooses the Sun as the default body and asks the user for two planets and graphs the positions of the three bodies for at least 100,000 days.

I have written the following code, but I only get a big blue rectangle in my graph every time I try to run it. Could you help me to correct and improve my code? Thanks a lot!

import numpy as np import matplotlib.pyplot as plt

print("============EL PROBLEMA DE LOS TRES CUERPOS============") print(" El programa tiene como objeto predeterminado el Sol") print("Seleccione dos planetas (Ej.- Para Mercurio, escriba el nnero ''1'')") #print(" Escriba el nmero 9 para salir para salir del programa") print("1.- Mercurio") print("2.- Venus") print("3.- Tierra") print("4.- Marte") print("5.- Jpiter") print("6.- Saturno") print("7.- Urano") print("8.- Neptuno")

def sol(): #Funciones que contienen la informacin de cada cuerpo masa = 1.989E30 r = 0 ao = 0 return masa, r, ao

def mer(): masa = 3.303E23 r = 57910 ao = 88 return masa, r, ao

def ven(): masa = 4.869E24 r = 108200 ao = 225 return masa, r, ao

def tie(): masa = 5.976E24 r = 149600 ao = 365 return masa, r, ao

def mar(): masa = 6.421E23 r = 227940 ao = 687 return masa, r, ao

def jup(): masa = 1.900E27 r = 778330 ao = 4332 return masa, r, ao

def sat(): masa = 5.688E26 r = 1429400 ao = 10760 return masa, r, ao

def ura(): masa = 8.686E25 r = 2870990 ao = 30681 return masa, r, ao

def nep(): masa = 1.024E26 r = 4504300 ao = 60190 return masa, r, ao

cuerpo1 = input("Primer cuerpo: ") #Pedimos al usuario dos planetas if cuerpo1 == '1': #de acuerdo al nmero que escriban c1 = mer() elif cuerpo1 == '2': c1 = ven() elif cuerpo1 == '3': c1 = tie() elif cuerpo1 == '4': c1 = mar() elif cuerpo1 == '5': c1 = jup() elif cuerpo1 == '6': c1 = sat() elif cuerpo1 == '7': c1 = ura() elif cuerpo1 == '8': c1 = nep()

cuerpo2 = input("Segundo cuerpo: ") if cuerpo2 == '1': c2 = mer() elif cuerpo2 == '2': c2 = ven() elif cuerpo2 == '3': c2 = tie() elif cuerpo2 == '4': c2 = mar() elif cuerpo2 == '5': c2 = jup() elif cuerpo2 == '6': c2 = sat() elif cuerpo2 == '7': c2 = ura() elif cuerpo2 == '8': c2 = nep()

c0 = sol() #Sacamos las variables de las tuplas de acuerdo a lo elegido

m0 = c0[0] m1 = c1[0] m2 = c2[0]

r0 = c0[1] r1 = c1[1] r2 = c2[1]

a1 = c1[2] a2 = c2[2]

G = 6.67430e-11 #Declaramos variables y condiciones iniciales secday = 24*3600 ti = 0 #Tiempo inicial y final de das a segundos tf = 100000*secday

xi0 = r0 #Posicin x inicial para Sol, planeta 1 y 2 xi1 = r1 xi2 = r2 yi0 = 0 #Posicin y inicial para Sol, planeta 1 y 2 yi1 = 0 yi2 = 0

velix0 = 0 #Velocidad inicial en 'x' y 'y' para Sol, planeta 1 y 2 velix1 = 0 velix2 = 0 veliy0 = 0 veliy1 = np.sqrt((G*m1) / r1) #Velocidad inicial: Velocidad orbital para los planetas veliy2 = np.sqrt((G*m2) / r2)

n = 100000 h = secday #Obtenemos la norma del vector r requerida rnorm1_1 = (np.sqrt((xi0-xi1)**2 + (yi0-yi1)**2))**3 rnorm1_2 = (np.sqrt((xi0-xi2)**2 + (yi0-yi2)**2))**3 rnorm2_1 = (np.sqrt((xi1-xi2)**2 + (yi1-yi2)**2))**3 rnorm2_2 = (np.sqrt((xi1-xi0)**2 + (yi1-yi0)**2))**3

rnorm3_1 = (np.sqrt((xi2-xi0)**2 + (yi2-yi0)**2))**3 rnorm3_2 = (np.sqrt((xi2-xi1)**2 + (yi2-yi1)**2))**3

#Definimos las ecuaciones para cada cuerpo def F0x(x,y): #Cuerpo: Sol return -(G*m1*(xi0-xi1)/rnorm1_1) - (G*m2*(xi0-xi2)/rnorm1_2) def F0y(x,y): return -(G*m1*(yi0-yi1)/rnorm1_1) - (G*m2*(yi0-yi2)/rnorm1_2)

def F1x(x,y): #Cuerpo: Planeta 1 return -(G*m1*(xi1-xi2)/rnorm2_1) - (G*m2*(xi1-xi0)/rnorm2_2) def F1y(x,y): return -(G*m1*(yi1-yi2)/rnorm2_1) - (G*m2*(yi1-yi0)/rnorm2_2)

def F2x(x,y): #Cuerpo: Planeta 2 return -(G*m1*(xi2-xi0)/rnorm3_1) - (G*m2*(xi2-xi1)/rnorm3_2) def F2y(x,y): return -(G*m1*(yi2-yi0)/rnorm3_1) - (G*m2*(yi2-yi1)/rnorm3_2)

T = np.arange(ti,tf+h,h) #Creamos listas donde guardaremos los datos n = len(T)

X0 = np.zeros_like(T) Y0 = np.zeros_like(T) X1 = np.zeros_like(T) Y1 = np.zeros_like(T) X2 = np.zeros_like(T) Y2 = np.zeros_like(T)

VX0 = np.zeros_like(T) VY0 = np.zeros_like(T) VX1 = np.zeros_like(T) VY1 = np.zeros_like(T) VX2 = np.zeros_like(T) VY2 = np.zeros_like(T)

X0[0] = xi0 #Definimos las funciones en cero Y0[0] = yi0 X1[0] = xi1 Y1[0] = yi1 X2[0] = xi2 Y2[0] = yi2

VX0[0] = velix0 VY0[0] = veliy0 VX1[0] = velix1 VY1[0] = veliy1 VX2[0] = velix2 VY2[0] = veliy2

for i in range (n-1): #Resolvemos las ecuaciones dif. con mtodo de Euler VX0[i+1] = VX0[i] + h * (F0x(X0[i],Y0[i])) VY0[i+1] = VY0[i] + h * (F0y(X0[i],Y0[i])) X0[i+1] = X0[i] + h * VX0[i+1] Y0[i+1] = Y0[i] + h * VY0[i+1] VX1[i+1] = VX1[i] + h * (F1x(X1[i],Y1[i])) VY1[i+1] = VY1[i] + h * (F1y(X1[i],Y1[i])) X1[i+1] = X1[i] + h * VX1[i+1] Y1[i+1] = Y1[i] + h * VY1[i+1] VX2[i+1] = VX2[i] + h * (F2x(X2[i],Y2[i])) VY2[i+1] = VY2[i] + h * (F2y(X2[i],Y2[i])) X2[i+1] = X2[i] + h * VX2[i+1] Y2[i+1] = Y2[i] + h * VY2[i+1]

plt.plot(X0,Y0,"r-") #Graficamos cada cuerpo plt.plot(X1,Y1,"g-") plt.plot(X2,Y2,"b-") plt.show()

Planeta Sol Mercurio Venus Tierra Marte Jpiter Saturno Urano Neptuno Masa kg) Distancia al Sol [km] Ao en das 1.989 E30 0 0 3.303 E23 57910 88 4.869 E24 108200 225 5.976 E24 149600 365 6.421 E23 227940 687 1.900 E27 778330 4332 5.688 E26 1429400 10760 8.686 E25 2870990 30681 1.024 E26 4504300 60190 Planeta Sol Mercurio Venus Tierra Marte Jpiter Saturno Urano Neptuno Masa kg) Distancia al Sol [km] Ao en das 1.989 E30 0 0 3.303 E23 57910 88 4.869 E24 108200 225 5.976 E24 149600 365 6.421 E23 227940 687 1.900 E27 778330 4332 5.688 E26 1429400 10760 8.686 E25 2870990 30681 1.024 E26 4504300 60190