Hi. Please help me with my activities. In task A, you have to answer the table. I will provide the picture of that. Don't answer this if you're not confident with it. If there are any errors, feel free to correct it to come up with the right answer. Thank you. Will rate helpful after reviewing. God bless.

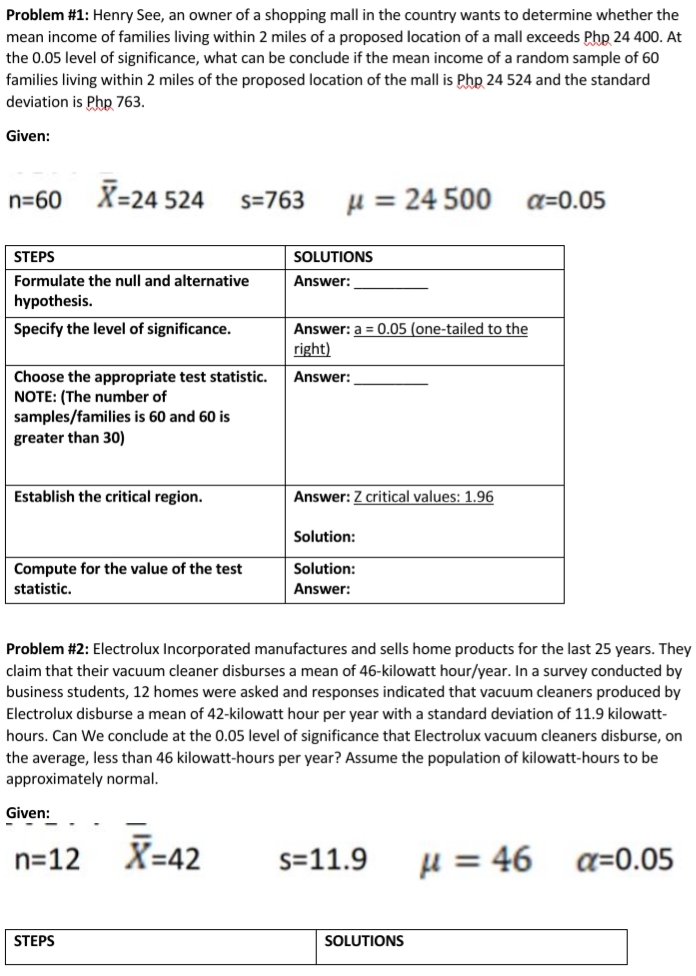
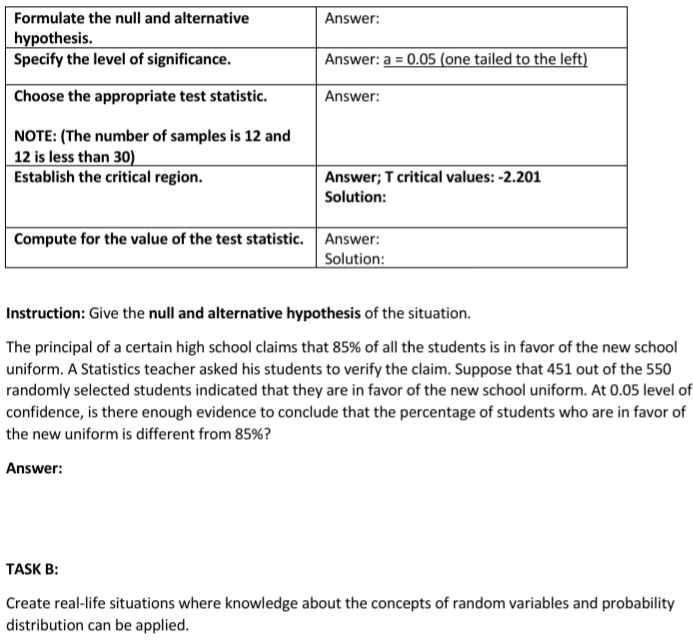
Problem #1: Henry See, an owner of a shopping mall in the country wants to determine whether the mean income of families living within 2 miles of a proposed location of a mall exceeds Php 24 400. At the 0.05 level of significance, what can be conclude if the mean income of a random sample of 60 families living within 2 miles of the proposed location of the mall is Php 24 524 and the standard deviation is Php 763. Given: n=60 X=24 524 s=763 / = 24 500 a=0.05 STEPS SOLUTIONS Formulate the null and alternative Answer: hypothesis. Specify the level of significance. Answer: a = 0.05 (one-tailed to the right) Choose the appropriate test statistic. Answer: NOTE: (The number of samples/families is 60 and 60 is greater than 30) Establish the critical region. Answer: Z critical values: 1.96 Solution: Compute for the value of the test Solution: statistic. Answer: Problem #2: Electrolux Incorporated manufactures and sells home products for the last 25 years. They claim that their vacuum cleaner disburses a mean of 46-kilowatt hour/year. In a survey conducted by business students, 12 homes were asked and responses indicated that vacuum cleaners produced by Electrolux disburse a mean of 42-kilowatt hour per year with a standard deviation of 11.9 kilowatt- hours. Can We conclude at the 0.05 level of significance that Electrolux vacuum cleaners disburse, on the average, less than 46 kilowatt-hours per year? Assume the population of kilowatt-hours to be approximately normal. Given: n=12 X=42 S=11.9 u = 46 a=0.05 STEPS SOLUTIONSFormulate the null and alternative Answer: hypothesis. Specify the level of significance. Answer: a = 0.05 (one tailed to the left) Choose the appropriate test statistic. Answer: NOTE: (The number of samples is 12 and 12 is less than 30) Establish the critical region. Answer; T critical values: -2.201 Solution: Compute for the value of the test statistic. Answer: Solution: Instruction: Give the null and alternative hypothesis of the situation. The principal of a certain high school claims that 85% of all the students is in favor of the new school uniform. A Statistics teacher asked his students to verify the claim. Suppose that 451 out of the 550 randomly selected students indicated that they are in favor of the new school uniform. At 0.05 level of confidence, is there enough evidence to conclude that the percentage of students who are in favor of the new uniform is different from 85%? Answer: TASK B: Create real-life situations where knowledge about the concepts of random variables and probability distribution can be applied