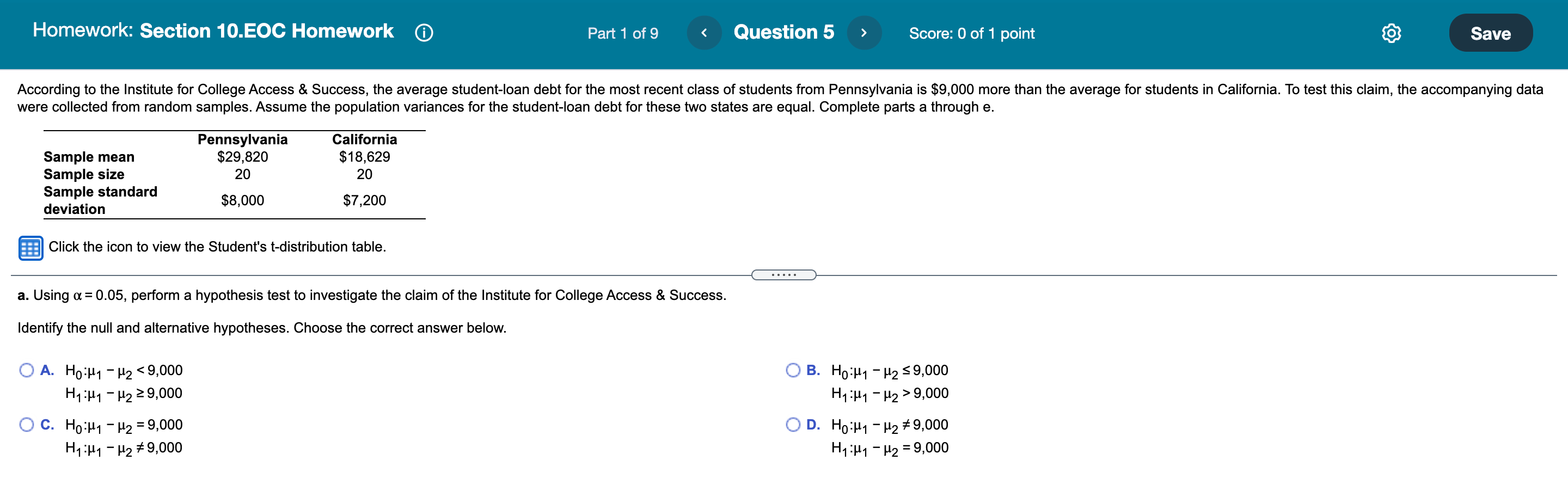
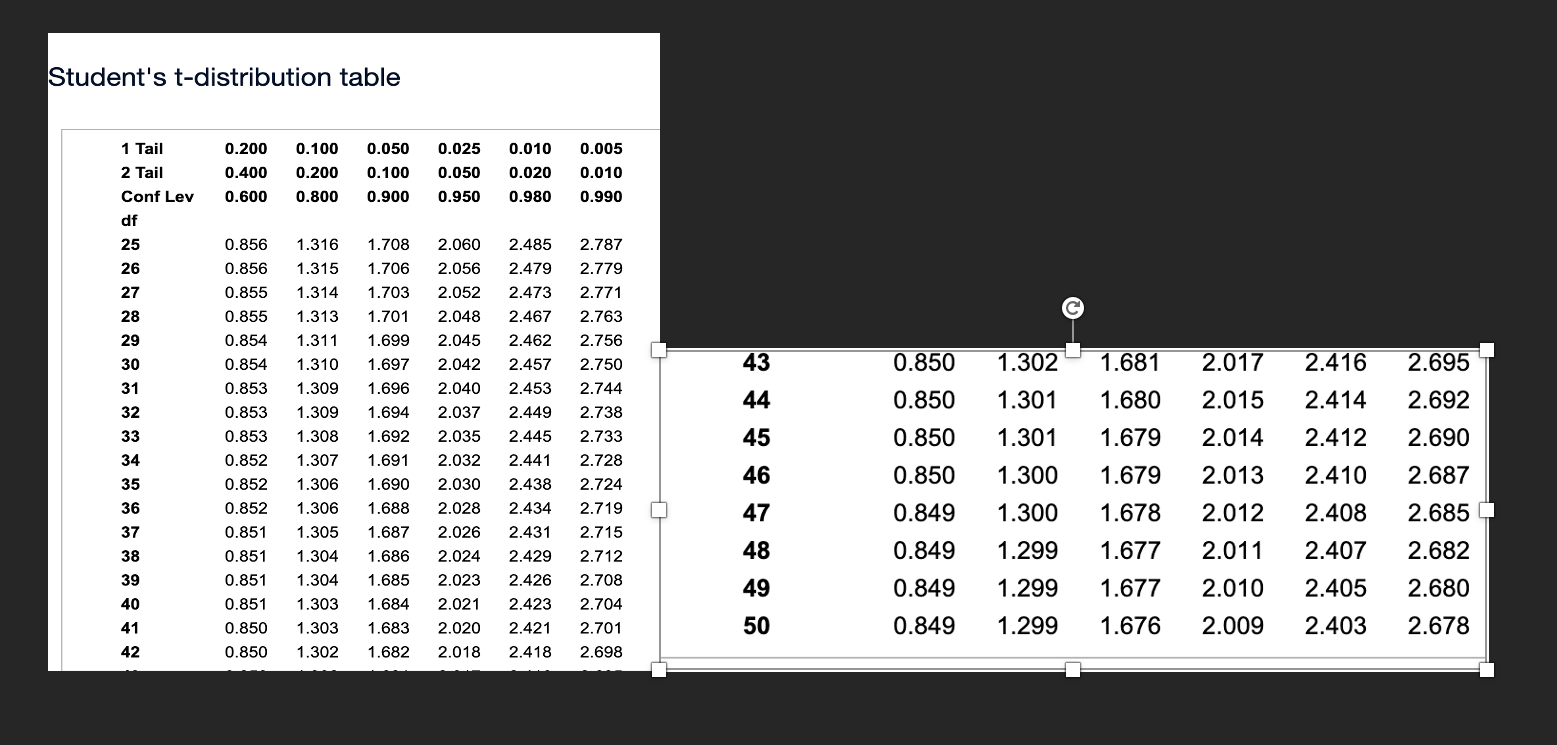
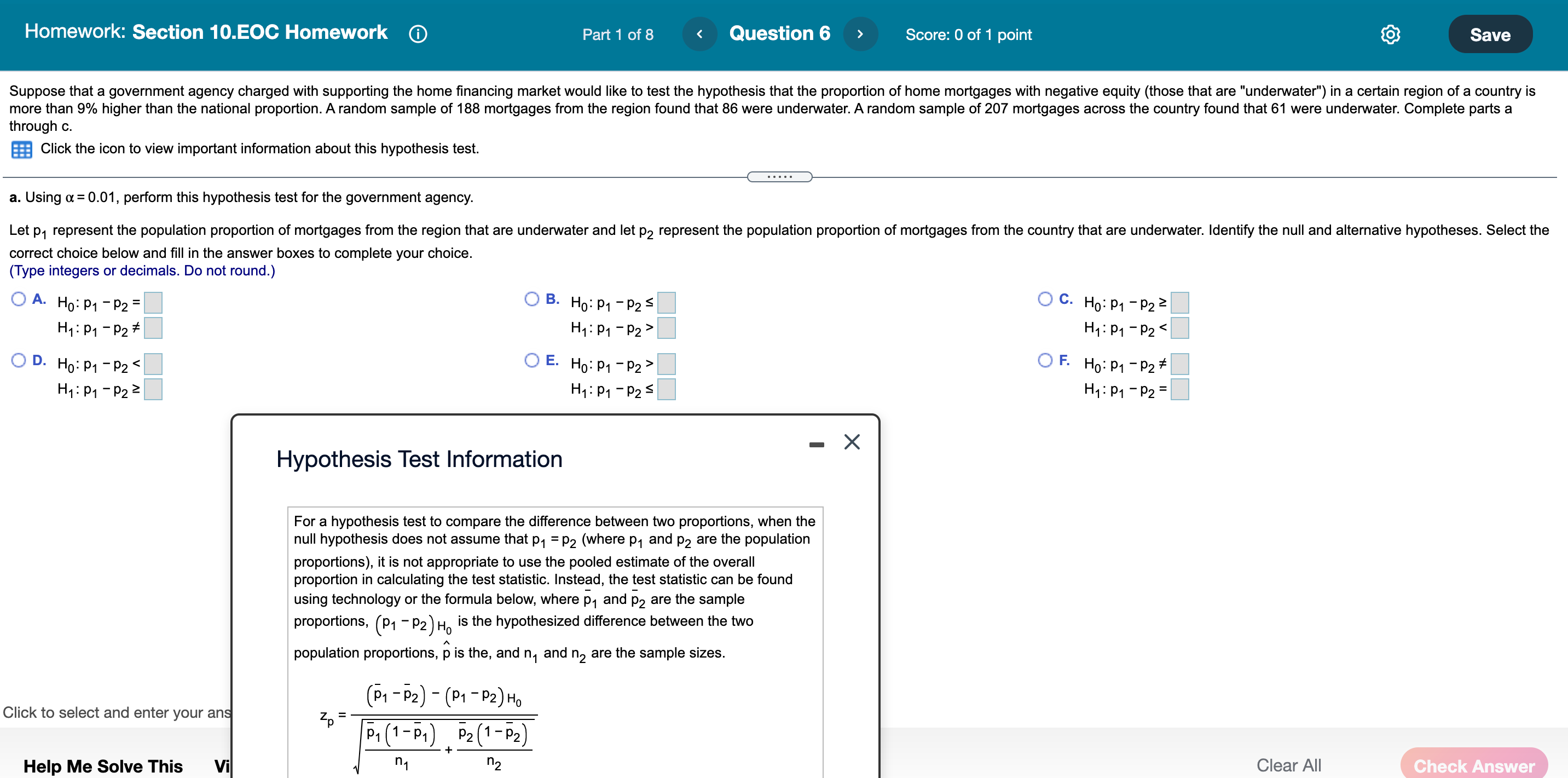
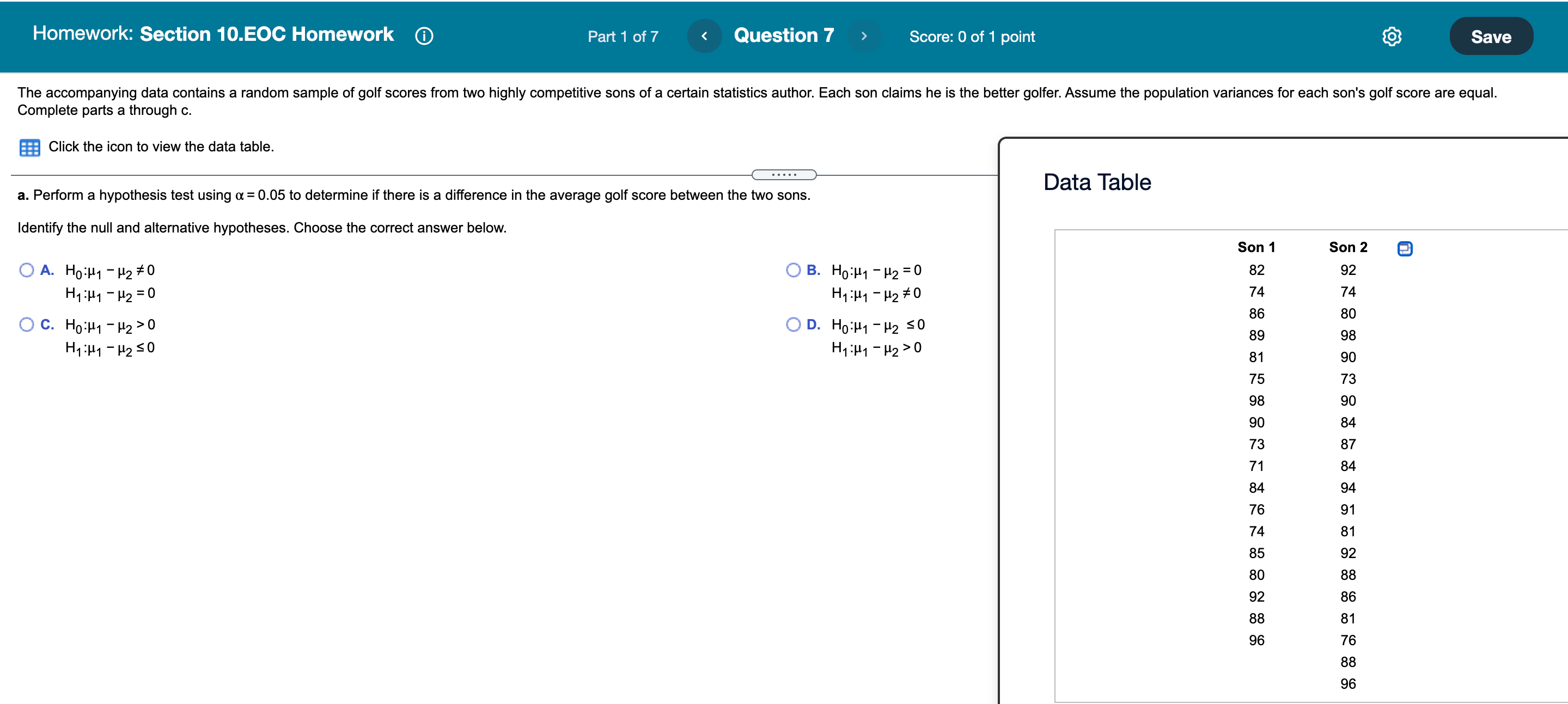
Homework: Section 10.EOC Homework Part 1 of 8 Question 2 Score: 0.33 of 1 point Save During the 2007-2008 decline in the housing market, it appeared that the average size of a newly constructed house fell. To investigate this trend, the square footages of a random sample of houses built in 2008 were compared to houses built in 2018. A random sample of 45 homes built in 2008 had a sample mean of 2,449.7 square feet and a sample standard deviation of 768.5 square feet. A random sample of 50 homes built in 2018 had a sample mean of 2,227.3 square feet and a sample standard deviation of 746.9 square feet. Assume that the population variances for the square footages of houses built in these two years are equal. Complete parts a through d. a. Using a = 0.05, perform a hypothesis test to determine if the average home constructed in 2008 was larger than a home built in 2018. Identify the null and alternative hypotheses. Choose the correct answer below. O A. HO:M1 - H2 so OB. HO:H1 - H2#0 H1: 1 1 - H 2 > 0 H1: H1 - 1 2 = 0 OC. HO:H1 -H2 20 OD. HO:M1 - H2 = 0 H1: 141 - H2 H1 : P1 - P2 = H1 : P1 - P2 2 H1 : P1 - P2 s OD. Ho: P1 - P2 2 OE. Ho: P1 - P2 S OF. Ho: P1 - P2 = H1 : P1 - P2 H1 : P1 - P2# - X Loan Data For-Profit Nonprofit X1 = 29 X2 = 12 n1 = 255 n2 = 235 Print DoneHomework: Section 10.EOC Homework (D Question 3 Score: 0 of1 point Pzer would like to test the effectiveness of a new cholesterol medication it has developed. To test the effectiveness, the LDL cholesterol level of 12 randomly selected individuals was measured before and after they took the medication The data is stored in the accompanying data table. Complete parts a through e below. Click here to view the data table. Click here to view the Student's ldistribution table. 8. Using a = 0.01, perform a hypothesis test to determine if the average LDL level is more than 50 points lower for patients who have taken the new medication. Identify the null and alternative hypotheses. Choose the correct answer below. OA. H: #50 OB. H2}! 250 ol'd 0 d H1zpd=50 H1:pd50 H1:pd#50 Homework: Section 10.EOC Homework Part 1 of 7 Question 4 Score: 0 of 1 point Save An interesting question is whether the strike zone for the batter in Baseball League A is different from the strike zone in Baseball League B. One way to address this question is to compare the percentage of called third strikes in the two leagues. To test this hypothesis, a random sample of plate appearances from each league was selected and the number of called third strikes was counted. The accompanying table shows the data. Complete parts a through c. Click the icon to view the third strike data. a. Perform a hypothesis test using a = 0.10 to determine if the proportion of called third strikes differs between the leagues. Let p, represent the population proportion of called third strikes in League A and let p2 represent the population proportion of called third strikes in League B. Identify the null and alternative hypotheses. Select the correct choice below and fill in the answer boxes to complete your choice. (Type integers or decimals. Do not round.) O A. Ho: P1 - P2 S OB. Ho: P1 - P2 H1 : P1 - P2> H1 : P1 - P2 2 H1: P1 - P2 s O D. Ho: P1 - P2 = OE. Ho: P1 - P2# OF. Ho: P1 - P2 2 H1 : P1 - P2# H1 : P1 - P2 = H1 : P1 - P2 9,000 O C. HO:H1 - H2 =9,000 OD. HO:H1 - H2 # 9,000 H1:H1 - H2 #9,000 H1:H1 - H2 =9,000Student's t-distribution table 1 Tail 0.200 0.100 0.050 0.025 0.010 0.005 2 Tail 0.400 0.200 0.100 0.050 0.020 0.010 Conf Lev 0.600 0.800 0.900 0.950 0.980 0.990 df 25 0.856 1.316 1.708 2.060 2.485 2.787 26 0.856 1.315 1.706 2.056 2.479 2.779 27 0.855 1.314 1.703 2.052 2.473 2.771 28 0.855 1.313 1.701 2.048 2.467 2.763 C 29 0.854 1.311 1.699 2.045 2.462 2.756 30 0.854 1.310 1.697 2.042 2.457 2.750 43 0.850 1.302 1.681 2.017 2.416 2.695 31 0.853 1.309 1.696 2.040 2.453 2.744 32 0.853 1.309 1.694 2.037 2.449 2.738 44 0.850 1.301 1.680 2.015 2.414 2.692 33 0.853 1.308 1.692 2.035 2.445 2.733 45 0.850 1.301 1.679 2.014 2.412 2.690 34 0.852 1.307 1.691 2.032 2.441 2.728 35 0.852 1.306 1.690 2.030 2.438 2.724 46 0.850 1.300 1.679 2.013 2.410 2.687 36 0.852 1.306 1.688 2.028 2.434 2.719 47 0.849 37 1.300 1.678 2.012 2.408 2.685 0.851 1.305 1.687 2.026 2.431 2.715 38 0.851 1.304 1.686 2.024 2.429 2.712 48 0.849 1.299 1.677 2.011 2.407 2.682 39 0.851 1.304 1.685 2.023 2.426 2.708 49 40 0.849 0.851 1.299 1.303 1.684 2.021 1.677 2.423 2.704 2.010 2.405 2.680 41 0.850 1.303 1.683 2.020 2.421 2.701 50 0.849 1.299 1.676 2.009 2.403 2.678 42 0.850 1.302 1.682 2.018 2.418 2.698Homework: Section 10.EOC Homework Part 1 of 8 Question 6 Score: 0 of 1 point Save Suppose that a government agency charged with supporting the home financing market would like to test the hypothesis that the proportion of home mortgages with negative equity (those that are "underwater") in a certain region of a country is more than 9% higher than the national proportion. A random sample of 188 mortgages from the region found that 86 were underwater. A random sample of 207 mortgages across the country found that 61 were underwater. Complete parts a through c. Click the icon to view important information about this hypothesis test. . . . . . a. Using a = 0.01, perform this hypothesis test for the government agency. Let p, represent the population proportion of mortgages from the region that are underwater and let p2 represent the population proportion of mortgages from the country that are underwater. Identify the null and alternative hypotheses. Select the correct choice below and fill in the answer boxes to complete your choice. (Type integers or decimals. Do not round.) O A. Ho: P1 - P2= O B. Ho: P1 - P2 s O C. Ho: P1 - P2 2 H1 : P1 - P2# H1 : P 1 - P2 > H1 : P1 - P2 OF. Ho: P1 - P2# H1 : P1 - P2 2 H1 : P1 - P2 s H1 : P1 - P2 = X Hypothesis Test Information For a hypothesis test to compare the difference between two proportions, when the null hypothesis does not assume that p1 = P2 (where p, and p2 are the population proportions), it is not appropriate to use the pooled estimate of the overall proportion in calculating the test statistic. Instead, the test statistic can be found using technology or the formula below, where p, and p2 are the sample proportions, (P1 - P2) Ho is the hypothesized difference between the two population proportions, p is the, and n, and n2 are the sample sizes. ( P1 - P2 ) - ( P1 - P2 ) Ho Click to select and enter your ans ZO = P 1 ( 1 - P 1 ) P2 ( 1 - P 2 ) Help Me Solve This Vi n1 n2 Clear All Check AnswerHomework: Section 10.EOC Homework Part 1 of 7 Question 7 > Score: 0 of 1 point Save The accompanying data contains a random sample of golf scores from two highly competitive sons of a certain statistics author. Each son claims he is the better golfer. Assume the population variances for each son's golf score are equal. Complete parts a through c. Click the icon to view the data table. Data Table a. Perform a hypothesis test using a = 0.05 to determine if there is a difference in the average golf score between the two sons. Identify the null and alternative hypotheses. Choose the correct answer below. Son 1 Son 2 O A. HO:H1 - H2 # 0 OB. HO:H1 - H2 = 0 82 92 H1: 1 1 - 12 = 0 H1: Hy - 12 # 0 74 74 86 80 O C. HO:M1 - H2 >0 OD. HO:M1 - H2 SO 89 98 H1: H1 - H2 50 H1: 1 1 - H 2 > 0 81 90 75 73 98 90 90 84 73 87 71 84 84 94 76 91 74 81 85 92 80 88 92 86 88 81 96 76 88 96


















