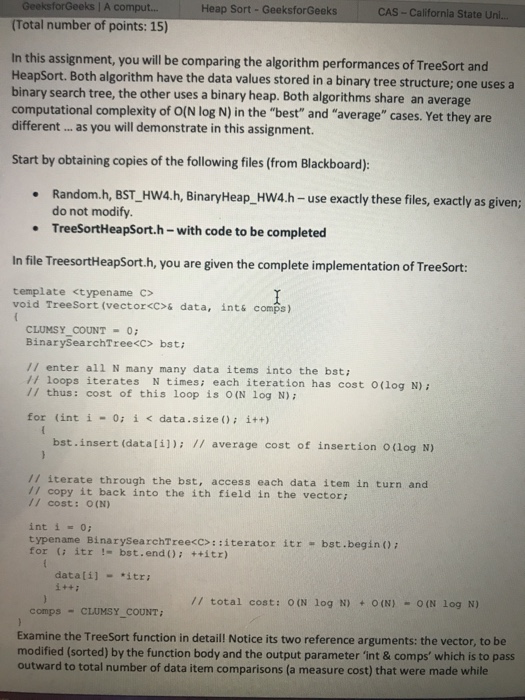
Homework Task 1: (5 pts) Complete the implementation of the HeapSort function, following the example of TreeSort. The binary heap data structure does not have an iterator, but based on your knowledge of the BinaryHeap interface, you should find a suitable alternative for what needs to happen.

#ifndef RANDOM_H_

#define RANDOM_H_

#include

#include

#include

#include

#include

using namespace std;

template

void rand_permute(Cont&);

void rand_seed()

{

int seed = static_cast(time(0));

srand(seed);

}

int rand_int(int a, int b)

{

return a + rand() % (b - a + 1);

}

vector rand_int_vector(int k, int a, int b)

{

set set_of_k;

vector rvec;

while (set_of_k.size()

{

int rv = rand_int(a,b);

set_of_k.insert(rv);

}

// will produce vector without duplicate values;

set::iterator itr = set_of_k.begin();

for (; itr != set_of_k.end(); ++itr)

rvec.push_back(*itr);

rand_permute(rvec);

return rvec;

}

template

void rand_permute(Cont& vals)

{

for (int i = 1; i

{

int r1 = rand_int(0,vals.size()-1);

int r2 = rand_int(0,vals.size()-1);

typename Cont::iterator itr1 = vals.begin();

typename Cont::iterator itr2 = vals.begin();

for (int i = 1; i

for (int i = 2; i

std::swap(*itr1,*itr2);

}

return;

}

#endif

----------------------------------------------------

#include

#include

#include

#include

#include "Random.h"

#include "TreeSortHeapSort.h"

using namespace std;

int main()

{

vector tosort1;

vector comps1;

vector comps2;

int sum1;

int sum2;

int numdata = 25;

rand_seed();

for (numdata = 10; numdata

{ sum1 = 0;

sum2 = 0;

for (int i = 1; i

{ tosort1 = rand_int_vector(numdata,1,1000);

vector tosort2(tosort1);

int k1,k2;

TreeSort(tosort1,k1);

assert(tosort1.size() == numdata);

HeapSort(tosort2,k2);

assert(tosort2.size() == numdata);

comps1.push_back(k1);

comps2.push_back(k2);

sum1 += k1;

sum2 += k2;

cout

double nlogn = numdata* log10(numdata)/log10(2); int nn = numdata * numdata;

double avg1 = (double)sum1 / 25;

double avg2 = (double)sum2 / 25;

cout

}

}

return 0;

}

-------------------------------------

#ifndef TSORTHSORT_H_

#define TSORTHSORT_H_

#include

#include

#include "BST_HW4.h"

#include "BinaryHeap_HW4.h"

using namespace std;

extern int CLUMSY_COUNT;

template

void TreeSort(vector& data, int& comps)

{

CLUMSY_COUNT = 0;

BinarySearchTree bst;

for (int i = 0; i

{

bst.insert(data[i]);

}

int i = 0;

typename BinarySearchTree::iterator itr = bst.begin();

for (; itr != bst.end(); ++itr)

{

data[i] = *itr;

i++;

}

comps = CLUMSY_COUNT;

}

template

void HeapSort(vector&data, int& comps)

{

CLUMSY_COUNT = 0;

// HW4: fill in to implement HeapSort;

comps = CLUMSY_COUNT;

}

#endif

--------------------------------------------------------------

#ifndef BINARYHEAP_H_

#define BINARYHEAP_H_

#include

#include "Vector.h"

using namespace std;

extern int CLUMSY_COUNT;

template

class BinaryHeap

{

public:

BinaryHeap()

: heap(100), currentSize(0)

{}

BinaryHeap(int capacity)

: heap(capacity), currentSize(0)

{}

BinaryHeap(const Vector&);

bool isEmpty() const

{

return currentSize == 0;

}

int size() const

{

return currentSize;

}

const C & findMin() const

{

return heap[1];

}

void insert(const C &);

void insert(C &&);

void deleteMin();

void deleteMin(C &);

void makeEmpty()

{

while (!heap.isEmpty())

heap.pop_back();

currentSize = 0;

}

void printHeap() const

{

printHeap(1,0);

}

private:

int currentSize;

Vector heap;

void buildHeap()

{

for (int i = currentSize/2; i > 0; i--)

percolateDown(i);

}

void percolateDown(int);

void printHeap(int,int) const;

};

template

BinaryHeap::BinaryHeap(const Vector& items)

: heap(items.size() + 10), currentSize(items.size())

{

for (int i = 0; i

heap[i + 1] = items[i];

buildHeap();

}

template

void BinaryHeap::insert(const C& x)

{

if (currentSize == heap.size()-1)

heap.resize(heap.size()*2);

int hole = ++currentSize;

C copy = x;

heap[0] = std::move(copy);

for (; x

{

CLUMSY_COUNT++;

heap[hole] = std::move(heap[hole/2]);

}

heap[hole] = std::move(heap[0]);

}

template

void BinaryHeap::insert(C&& x)

{

if (currentSize == heap.size()-1)

heap.resize(heap.size()*2);

int hole = ++currentSize;

C copy = x;

heap[0] = std::move(copy);

for (; x

heap[hole] = std::move(heap[hole/2]);

heap[hole] = std::move(heap[0]);

}

template

void BinaryHeap::deleteMin()

{

assert(!isEmpty());

heap[1] = std::move(heap[currentSize--]);

percolateDown(1);

}

template

void BinaryHeap::deleteMin(C & minItem)

{

assert(!isEmpty());

minItem = std::move(heap[1]);

heap[1] = std::move(heap[currentSize--]);

percolateDown(1);

}

template

void BinaryHeap::percolateDown(int hole)

{

int child;

C tmp = std::move(heap[hole]);

for (; hole * 2

{

CLUMSY_COUNT++;

child = hole * 2;

if (child != currentSize && heap[child + 1]

child++;

if (heap[child]

heap[hole] = std::move(heap[child]);

else

break;

}

heap[hole] = std::move(tmp);

}

template

void BinaryHeap::printHeap(int index, int offset) const

{

if (index > currentSize)

return;

for (int i = 1; i

cout

cout

printHeap(2*index, offset + 1);

printHeap(2*index+1, offset + 1);

return;

}

#endif

-----------------------------------------------------------------------------------------------------------

#ifndef BINARY_SEARCH_TREE_H

#define BINARY_SEARCH_TREE_H

//#include "dsexceptions.h"

#include

#include

#include

#include

using namespace std;

int CLUMSY_COUNT = 0;

template

class BinarySearchTree

{

private:

struct BinaryNode

{

C element;

BinaryNode *left;

BinaryNode *right;

BinaryNode *parent;

BinaryNode(const C & elem, BinaryNode *lt,

BinaryNode *rt,

BinaryNode *par)

: element(elem), left(lt), right(rt), parent(par)

{}

};

public:

//struct BinaryNode;

class iterator

{public:

iterator() : current{nullptr}

{}

iterator(BinaryNode * t) : current(t)

{}

C & operator *() const

{

return current->element;

}

bool operator ==(iterator other) const

{

return current == other.current;

}

bool operator != (iterator other) const

{

return current != other.current;

}

iterator & operator ++()

{

if (is_root(current))

current = leftmost(current->right);

else if (is_left_child(current))

{

if (current->left == nullptr && current->right

== nullptr)

{

current = current->parent;

CLUMSY_COUNT++;

}

else if (current->right != nullptr)

current = leftmost(current->right);

else

{

//; // should not happen

current = current->parent; // NEW!!

CLUMSY_COUNT++;

}

}

else if (is_right_child(current))

{

if (current->right != nullptr)

current = leftmost(current->right);else

current = follow_parent_until_leftchild(current);

}

return *this;

}

iterator & operator++(int)

{

iterator old(*this);

++(*this);

return old;

}

protected:

BinaryNode * current;

/*

bool is_right_child(BinaryNode * t)

{

return (t != nullptr && t->parent == nullptr);

}

*/

bool is_root(BinaryNode *t)

{

return (t != nullptr && t->parent == nullptr);

}

bool is_left_child(BinaryNode *t)

{

assert(t != nullptr);

if (t->parent != nullptr && t->parent->left == t)

return true;

else

return false;

}

bool is_right_child(BinaryNode *t)

{

assert(t != nullptr);

if (t->parent != nullptr && t->parent->right ==

t)

return true;

else

return false;

}

BinaryNode * leftmost(BinaryNode *t)

{

if (t == nullptr)

return nullptr;

CLUMSY_COUNT++;

if (t->left == nullptr)

return t;

return leftmost(t->left);

}

BinaryNode * follow_parent_until_leftchild(BinaryNode *t)

{

if (is_root(t))

return nullptr;

CLUMSY_COUNT++;

if (is_left_child(t))

return t->parent;

return follow_parent_until_leftchild(t->parent);

}

friend class BinarySearchTree;

};

public:

BinarySearchTree( ) : root{ nullptr }

{

}

BinarySearchTree( const BinarySearchTree & rhs ) : root{ nullptr }

{

root = clone( rhs.root);

}

BinarySearchTree( BinarySearchTree && rhs ) : root{ rhs.root }

{

rhs.root = nullptr;

}

~BinarySearchTree( )

{

makeEmpty( );

}

BinarySearchTree & operator=( const BinarySearchTree & rhs )

{

BinarySearchTree copy = rhs;

std::swap( *this, copy );

return *this;

}

BinarySearchTree & operator=( BinarySearchTree && rhs )

{

std::swap( root, rhs.root );

return *this;

}

const C & findMin( ) const

{

assert(!isEmpty());

return findMin( root )->element;

}

const C & findMax( ) const

{

assert(!isEmpty());

return findMax( root )->element;

}

bool contains( const C & x ) const

{

return contains( x, root );

}

bool isEmpty( ) const

{

return root == nullptr;

}

void printTree( ostream & out = cout ) const

{

if( isEmpty( ) )

out

else

printTree( root, out );

}

void printInternal()

{

printInternal(root,0);

}

void makeEmpty( )

{

makeEmpty( root );

}

iterator insert( const C & x )

{

return insert( x, root, root);

}

iterator insert( C && x )

{

return insert( std::move( x ), root, root);

}

void remove( const C & x )

{

remove( x, root );

}

iterator begin() const

{

BinaryNode *t = root;

while (t->left != nullptr)

t = t->left;

iterator beg(t);

return beg;

}

iterator end() const

{

iterator theend(nullptr);

return theend;

}

int size() const

{

if (root == nullptr)

return 0;

return 1 + size(root->left) + size(root->right);

}

private:

BinaryNode *root;

iterator insert( const C & x, BinaryNode * & t,

BinaryNode * & par )

{

if( t == nullptr )

{

t = new BinaryNode{ x, nullptr, nullptr, par };

return iterator(t);

}

else if( x element )

{

CLUMSY_COUNT++;

return insert( x, t->left, t );

}

else if( t->element

{

CLUMSY_COUNT++;

return insert( x, t->right, t );

}

else

return iterator(t); // Duplicate; do nothing

}

iterator insert( C && x, BinaryNode * & t, BinaryNode *

& par )

{

if( t == nullptr )

{

t = new BinaryNode{ std::move( x ), nullptr,

nullptr, par };

return iterator(t);

}

else if( x element )

return insert( std::move( x ), t->left, t );

else if( t->element

return insert( std::move( x ), t->right, t );

else

return iterator(t); // Duplicate; do nothing

}

void remove( const C & x, BinaryNode * & t )

{

if( t == nullptr )

return;

// Item not found; do nothing

if( x element )

remove( x, t->left );

else if( t->element

remove( x, t->right );

else if( t->left != nullptr && t->right !=

nullptr ) // Two children

{

t->element = findMin( t->right )->element;

remove( t->element, t->right );

}

else{

BinaryNode *oldNode = t;

if (t->left != nullptr)

{

t->left->parent = t->parent;

t = t->left;

}

else

{

if (t->right != 0)

t->right->parent = t->parent;

t = t->right;

}

delete oldNode;

}

}

BinaryNode * findMin( BinaryNode *t ) const

{

if( t == nullptr )

return nullptr;

if( t->left == nullptr )

return t;

return findMin( t->left );

}

BinaryNode * findMax( BinaryNode *t ) const

{

if( t != nullptr )

while( t->right != nullptr )

t = t->right;

return t;

}

bool contains( const C & x, BinaryNode *t ) const

{

if( t == nullptr )

return false;

else if( x element )

return contains( x, t->left );

else if( t->element

return contains( x, t->right );

else

return true;

// Match

}

void makeEmpty( BinaryNode * & t )

{

if( t != nullptr )

{

makeEmpty( t->left );

makeEmpty( t->right );

delete t;

}

t = nullptr;

}

void printTree( BinaryNode *t, ostream & out )

const

{

if( t != nullptr )

{

printTree( t->left, out );out element

printTree( t->right, out );

}

}

void printInternal(BinaryNode* t, int offset)

{

for(int i = 1; i

cout

if (t == nullptr)

{

cout

return;

}

cout element

printInternal(t->left, offset + 1);

printInternal(t->right, offset + 1);

}

BinaryNode * clone1(BinaryNode *t) const

{

if (t == nullptr)

return nullptr;

else

return new BinaryNode(t->element, clone1(t->left),

clone1(t->right), nullptr);

}

void put_parents(BinaryNode * t, BinaryNode * par)

const

{

if (t == nullptr)

return;

t->parent = par;

if (t->left != nullptr)

put_parents(t->left, t);

if (t->right != nullptr)

put_parents(t->right, t);

}

BinaryNode * clone(BinaryNode *t) const

{

BinaryNode * theclone = clone1(t);

put_parents(theclone, nullptr);

return theclone;

}

int size(BinaryNode* t) const

{

if (t == nullptr)

return 0;

return 1 + size(t->left) + size(t->right);

}

};

#endif

GeeksforGeeks | A c (Total number of points: 15) Heap Sort-GeeksforGeeks CAS-California State Uni In this assignment, you will be comparing the algorithm performances of TreeSort and Heapsort. Both algorithm have the data values stored in a binary tree structure; one uses a binary search tree, the other uses a binary heap. Both algorithms share an average computational complexity of O(N log N) in the "best" and "average" cases. Yet they are different .. as you will demonstrate in this assignment. Start by obtaining copies of the following files (from Blackboard): Random.h, BST_HW4.h, BinaryHeap_HW4.h-use exactly these files, exactly as given; do not modify. TreeSortHeapSort.h-with code to be completed In file TreesortHeapSort.h, you are given the complete implementation of TreeSort: template void TreeSort (vector& data, int& comps) CLUMSY_COUNT 0: BinarySearchTree bst: // enter all N many many data items into the bst: // loops iterates N timesi each iteration has cost o(log N) // thus: cost of this loop is O (N log N) for (int i-0; ::iterator itr bst.begin for ( itr bst.end)i ++itr) data[i] itr // total cost: o (N log N)O(N) -O(N log N) comps- CLUMSY COUNT: Examine the TreeSort function in detaill Notice its two reference arguments: the vector, to be modified (sorted) by the function body and the output parameter 'int & comps' which is to pass outward to total number of data item comparisons (a measure cost) that were made while