Question

1 Approved Answer

Posted on Feb 27, 2024

HOW DO YOU SOLVE THIS PROBLEM ON EXCEL? 1. The solution of LP2 should have subtours with multiple arcs.(If instead you get a solution with

HOW DO YOU SOLVE THIS PROBLEM ON EXCEL?

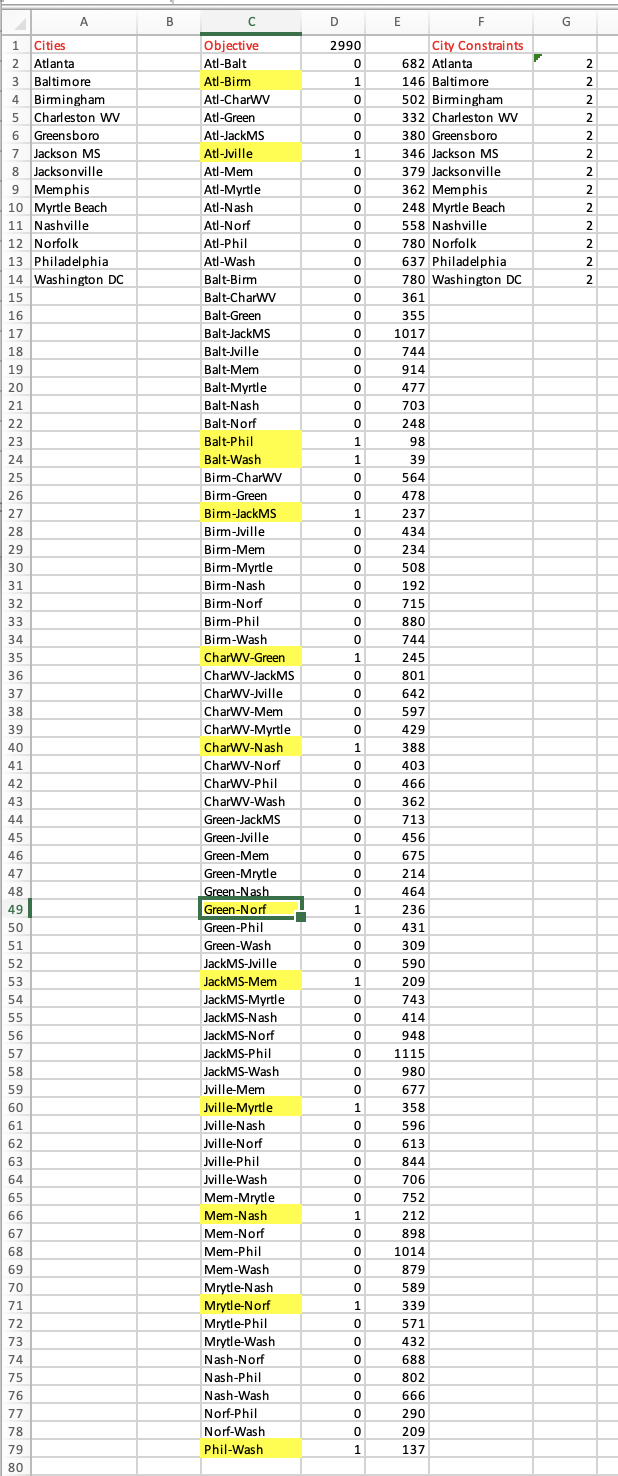
1. The solution of LP2 should have subtours with multiple arcs.(If instead you get a solution with more arcs with values greater than 1, then add constraints to eliminate these.)The fun (and somewhat time-consuming) part of the project is using the arcs whose values are equal to 1 to identify the subtours in your solution (e.g. if the first arc = 1, then a tour goes directly from Atlanta to Baltimore). Identifying the positive decision variables and connecting the corresponding cities will reveal the subtours that make up the solution to LP2.Find the smallest of these subtours and add a constraint to eliminate it.

For example: if cells D2, D3 and D14 all equal 1, this would give a subtour from Atlanta to Baltimore (D2) to Birmingham (D14) and back to Atlanta (D3). You would eliminate this by putting the formula =D2+D3+D14 into a cell on your spreadsheet, say G15, and then adding the constraint G15Specify the smallest subtour that you found by listing the 3 cities included in this tour (similar to the one in the example above: Atlanta to Baltimore to Birmingham to Atlanta, except that the 3-city subtour that you find makes geographic sense!).

Subtour:

2. Create a constraint to eliminate the subtour identified in the previous question and re-solve the LP relaxation. Give the optimal objective function of the new LP (LP3).

Optimal objective function value of LP3:

3. Repeat the process you just stepped through to identify the smallest subtour from LP3 (it should be similar to the one you just eliminated, but with 4 cities included instead of 3). Add a constraint to eliminate this subtour (since it has 4 cities, your constraint should require that the sum of the 4 arcs in the subtour must be). List the arcs in this subtour. After adding the new constraint, solve the resulting LP (LP4) and record its objective function value.

Arcs in subtour of LP3:

Optimal objective function value of LP4:

4. Repeat question 3 two more times. You should find two subtours that are very similar to the one you identified in the previous question. In fact, they should connect the same 4 cities. Identify the similar subtour in LP4 (by listing its arcs), add the constraint to eliminate it, and record the objective function value of LP5. Do the same thing to identify a subtour in LP5, eliminate it, and give the objective function value of the resulting LP6.

Arcs in subtour of LP4:

Optimal objective function value of LP5:

Arcs in subtour of LP5:

Optimal objective function value of LP6:

5. Considering the similarities of the previous three subtours that you had to eliminate one at a time, develop a better constraint (and a better approach) that could eliminate all of the subtours connecting the same 4 cities all at once?

6. The point of the previous question is that a single constraint could eliminate all subtours connecting the same 4 cities. Sadly, the total number of possible subtour constraints is combinatorial.How many sets of 4-city groupings would there be out of 13 total cities? This number might not seem so huge. But it ramps up quickly. How many sets of 10-city groupings would there be for a TSP with 100 total cities?

7. See if you can find the optimal solution to the 13-city TSP by continuing to eliminate subtours. After solving LP6, all that should be needed is to identify arcs whose LP6 solution value equals 2 and add the constraints to ensure they are. See what you can come up with as your best tour, either by continuing to add subtour constraints or by building one yourself using what you have learned from the LP solutions. Provide the tour (e.g Atlanta to Birmingham to ...), along with its associated costs.