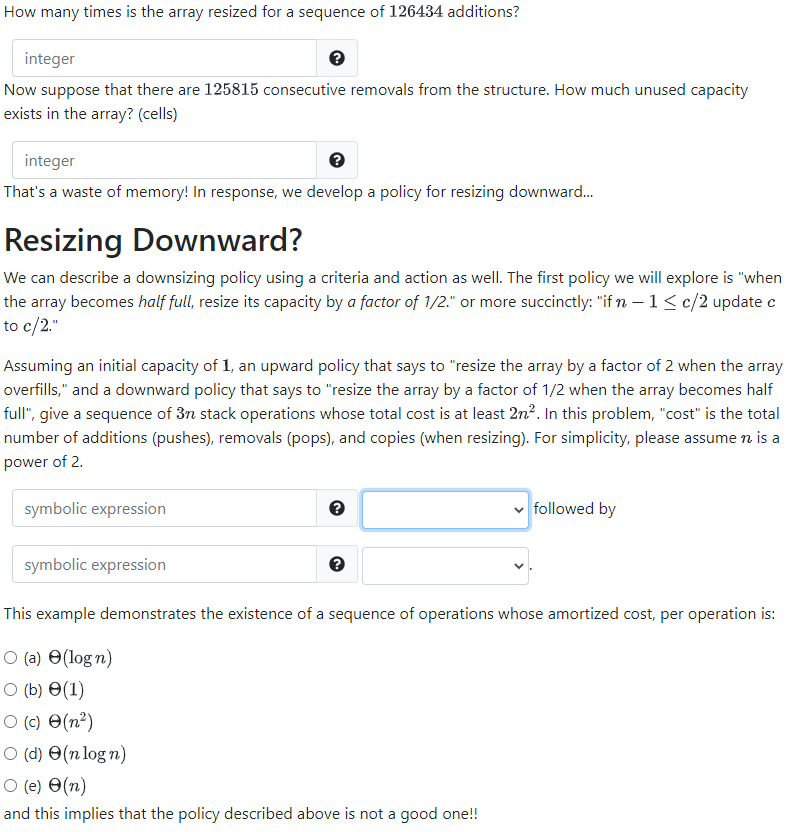
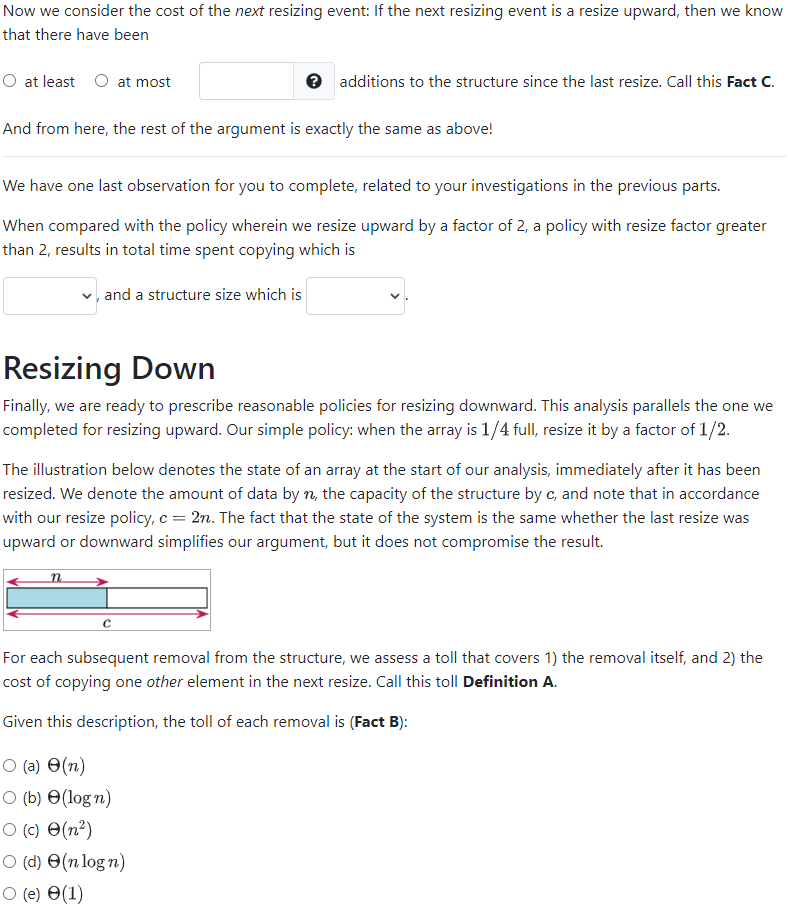
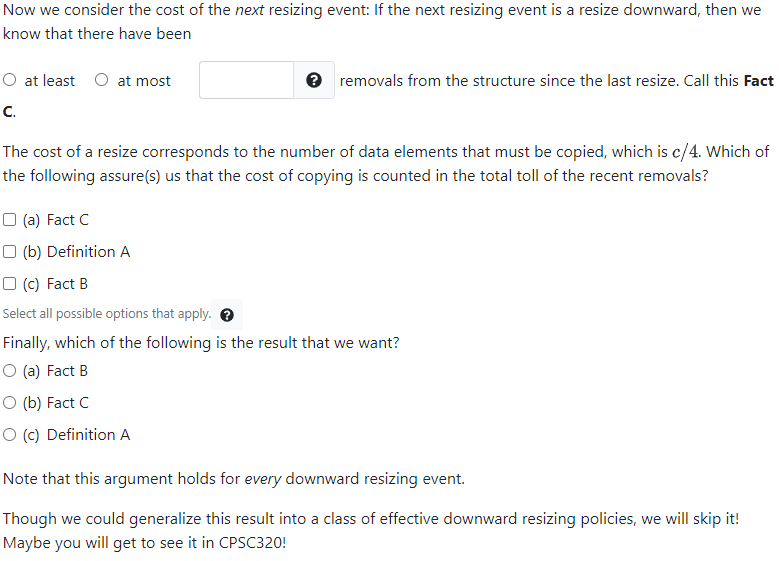
Question 5: Array Resizing In class we explored a bit of the theory behind resizing arrays. While our discussion was motivated by the C++ implementation of the vector, and though we discussed it in the context of ADT Stack, the ideas contained in the analysis are powerful and worth understanding deeply and more generally. They apply to any structure implemented using blocks of contiguous memory, and they also serve as a perfect application of a new analysis tool that you'll use in CPSC320: Amortized Analysis. In this question we examine the problem of array resizing from a slightly different perspective, and we use that new approach to devise a resizing policy that we can use for resizing downward, as well as upward. In the end, we generalize our discoveries so we understand the class of policies that will give us the same asymptotic results. The resizing problem is, fundamentally, an analysis of the trade-off between the cost of computation, and the space used by a structure. In this problem, we wish to bound both of these features by some constant factor of the number of operations performed (additions and removals) over the lifetime of the structure. Preliminaries We start by reviewing the results that we explored in class. Consider a sequence of additions to an array, beginning with an empty array of capacity 1. Suppose that our growth resize policy is as follows: When the array overfills, 1. Create a new array whose capacity is twice the original. 2. Copy all existing data into the new array. 3. Free the space associated with the old array. 4. Rename the new array, using the old name. After the resize, we add the new data element to the array. Note that the copy step requires n copies where n is the amount of data the array contains before the addition. We can describe the policy more succinctly as: "if n+1 > c update c to 2c" where c is the capacity of the array. The criteria for resizing is that the array becomes overfull (n+1> c) and the action is to double the capacity (c = 2c). How many times is the array resized for a sequence of 126434 additions? integer Now suppose that there are 125815 consecutive removals from the structure. How much unused capacity exists in the array? (cells) integer That's a waste of memory! In response, we develop a policy for resizing downward... Resizing Downward? We can describe a downsizing policy using a criteria and action as well. The first policy we will explore is "when the array becomes half full, resize its capacity by a factor of 1/2." or more succinctly: "if n - 1 c/2 update c to c/2." Assuming an initial capacity of 1, an upward policy that says to "resize the array by a factor of 2 when the array overfills," and a downward policy that says to "resize the array by a factor of 1/2 when the array becomes half full", give a sequence of 3n stack operations whose total cost is at least 2n. In this problem, "cost" is the total number of additions (pushes), removals (pops), and copies (when resizing). For simplicity, please assume n is a power of 2. symbolic expression symbolic expression followed by This example demonstrates the existence of a sequence of operations whose amortized cost, per operation is: (a) O(logn) (b) (1) (c) (n) O (d) (nlogn) (e) e(n) and this implies that the policy described above is not a good one!! Resizing Up (reprise) To design a good policy for resizing downward, it will help us to understand our basic resize upward policy in more detail: In class, we assessed the cost of an upward resizing policy by considering a (large) sequence of additions to the structure, adding up the total cost of copying data during the additions, and then dividing to find the average cost per operation (aka "amortised cost"). In this analysis, we still want to assess the cost of a policy, but we will do it by focussing on the cost of each resize event, and allowing for any sequence of additions and removals. In each of the statements below, answer the questions to complete a proof that our basic policy for resizing upward (double when full) is a good one. That is, that a resizing event costs no more than a constant amount of time per operation, on average. In another part of the problem we will argue that our space used is no more than a constant times the amount of data contained in the structure. The illustration below denotes the state of an array at the start of our analysis, immediately after it has been resized. We denote the amount of data by n, the capacity of the structure by c, and note that in accordance with our resize policy, c = 2n. n C For each subsequent addition to the structure, we assess a toll that covers 1) the addition itself, 2) the cost of copying the new addition in the next resize, and 3) the cost of copying one other element in the next resize. Call this toll Definition A. Given this description, the toll of each addition is (Fact B): (a) O(n) (b) O(logn) (c) O(n) (d) O(nlogn) (e) (1) Now we consider the cost of the next resizing event: If the next resizing event is a resize upward, then we know that there have been O at least O at most additions to the structure since the last resize. Call this Fact C. The cost of a resize corresponds to the number of data elements that must be copied, which is c. Which of the following assure(s) us that the cost of copying is counted in the total toll of the recent additions? (a) Fact C (b) Definition A (c) Fact B Select all possible options that apply. Finally, which of the following is the result that we want? (a) Fact B (b) Fact C (c) Definition A Note that this argument holds for every upward resizing event. To show us that you understand this argument, we would like you to do the same analysis for a policy whose action is to increase the size of the array by a factor of 3.3 when the array fills. The illustration below denotes the state of an array at the start of our analysis, immediately after it has been resized. We denote the amount of data by n, the capacity of the structure by c, and note that in accordance with our resize policy, c = 3.3n. C For each subsequent addition to the structure, we assess a toll that covers 1) the addition itself, 2) the cost of copying the new addition in the next resize, and 3) the cost of copying in the next resize. Call this toll Definition A. Given this description, the toll of each addition is (Fact B): (a) O(n) (b) O(logn) (c) O(n) (d) O(nlogn) (e) (1) other element(s) Now we consider the cost of the next resizing event: If the next resizing event is a resize upward, then we know that there have been O at least at most additions to the structure since the last resize. Call this Fact C. And from here, the rest of the argument is exactly the same as above! We have one last observation for you to complete, related to your investigations in the previous parts. When compared with the policy wherein we resize upward by a factor of 2, a policy with resize factor greater than 2, results in total time spent copying which is and a structure size which is Resizing Down Finally, we are ready to prescribe reasonable policies for resizing downward. This analysis parallels the one we completed for resizing upward. Our simple policy: when the array is 1/4 full, resize it by a factor of 1/2. The illustration below denotes the state of an array at the start of our analysis, immediately after it has been resized. We denote the amount of data by n, the capacity of the structure by c, and note that in accordance with our resize policy, c = 2n. The fact that the state of the system is the same whether the last resize was upward or downward simplifies our argument, but it does not compromise the result. n C For each subsequent removal from the structure, we assess a toll that covers 1) the removal itself, and 2) the cost of copying one other element in the next resize. Call this toll Definition A. Given this description, the toll of each removal is (Fact B): O (a) (n) (b) (logn) (c) (n) (d) O(nlogn) O (e) (1) Now we consider the cost of the next resizing event: If the next resizing event is a resize downward, then we know that there have been O at least at most removals from the structure since the last resize. Call this Fact C. The cost of a resize corresponds to the number of data elements that must be copied, which is c/4. Which of the following assure(s) us that the cost of copying is counted in the total toll of the recent removals? (a) Fact C (b) Definition A (c) Fact B Select all possible options that apply. Finally, which of the following is the result that we want? (a) Fact B (b) Fact C O (c) Definition A Note that this argument holds for every downward resizing event. Though we could generalize this result into a class of effective downward resizing policies, we will skip it! Maybe you will get to see it in CPSC320! Conclusion, and Space In the last two parts, we have shown that we can resize upward and downward, each with constant average cost per operation. Since we can do it for both types of resizing, the result holds over the lifetime of the structure! Given the two policies: 1) if the array fills, resize upward by a factor of two, and 2) if the array is ever less than 1/4 full, resize downward by a factor of 1/2, we know that: c n, and where c is the capacity of the array, and n is the amount of data it contains. Thus, our structure always has size which is: (a) (logn) (b) (1) (c) O(n) (d) O(nlogn) (e) e(n) YAY!