How to solve \ \ lines. Here are the values of the variables

y=

number of culs-de-sac and

z=

number of intersections:\ \\\\table[[

y

,1,0,1,0,0,2,0,1,1,1,2,1,0,0,1,1,0,1,1,1,1,0,0,0],[

z

,1,8,6,1,1,5,3,0,0,4,4,0,0,1,2,1,4,0,4,0,3,0,1,1],[

y

,1,1,2,0,1,2,2,1,1,0,2,1,1,0,1,5,0,3,0,1,1,0,0,],[

z

,0,1,3,2,4,6,6,0,1,1,8,3,3,5,0,5,2,3,1,0,0,0,3,]]\ (a) Construct a histogram for the

y

data.\ What proportion of these subdivisions had no culs-de-sac? At least one cul-de-sac? (Round your answers to three decimal places.)\ no culs-de-sac\ (No Response) (No Response)\ at least one cul-de-sac\ (No Response)

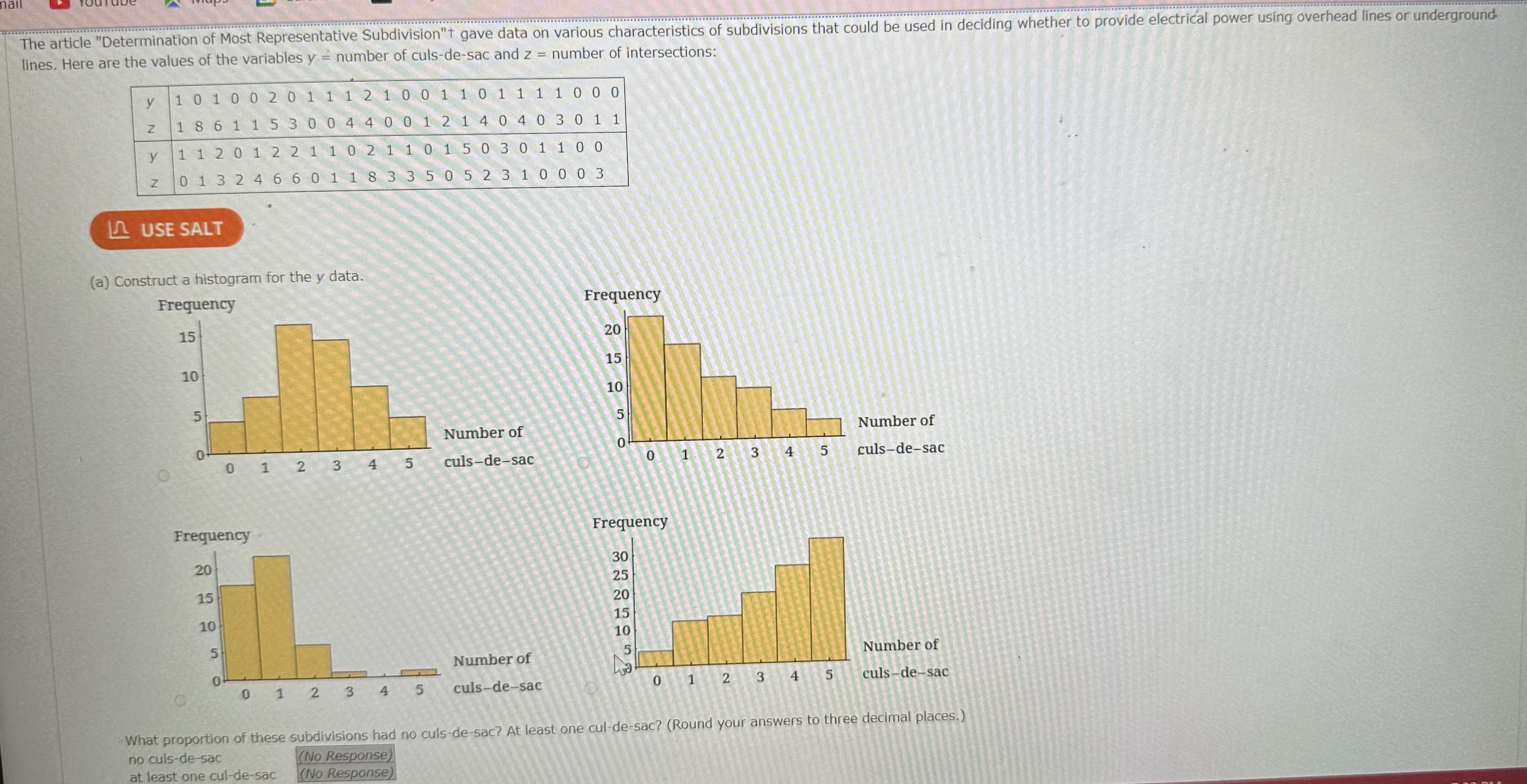
es. Here are the values of the variables y= number of culs-de-sac and z= number of intersections: \begin{tabular}{|l|llllllllllllllllllllllll|} \hliney & 1 & 0 & 1 & 0 & 0 & 2 & 0 & 1 & 1 & 1 & 2 & 1 & 0 & 0 & 1 & 1 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \\ z & 1 & 8 & 6 & 1 & 1 & 5 & 3 & 0 & 0 & 4 & 4 & 0 & 0 & 1 & 2 & 1 & 4 & 0 & 4 & 0 & 3 & 0 & 1 & 1 \\ \hliney & 1 & 1 & 2 & 0 & 1 & 2 & 2 & 1 & 1 & 0 & 2 & 1 & 1 & 0 & 1 & 5 & 0 & 3 & 0 & 1 & 1 & 0 & 0 \\ z & 0 & 1 & 3 & 2 & 4 & 6 & 6 & 0 & 1 & 1 & 8 & 3 & 3 & 5 & 0 & 5 & 2 & 3 & 1 & 0 & 0 & 0 & 3 \\ \hline \end{tabular} (a) What proportion of these subdivisions had no culs-de-sac? At least one no culs-de-sac