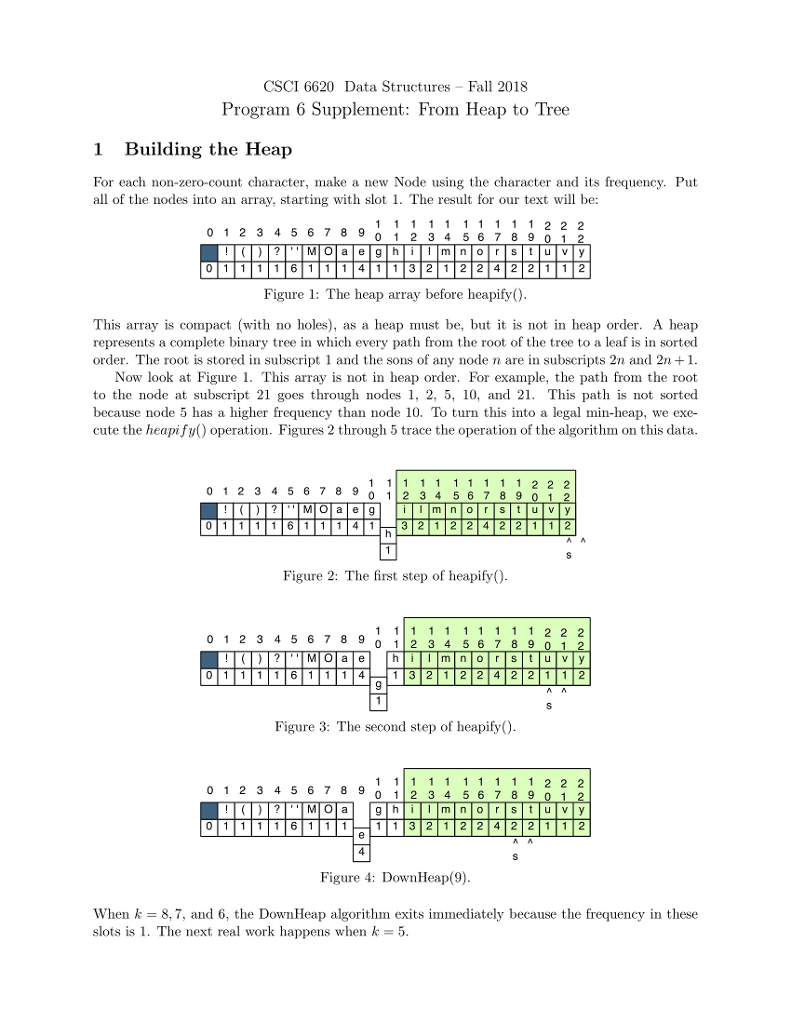
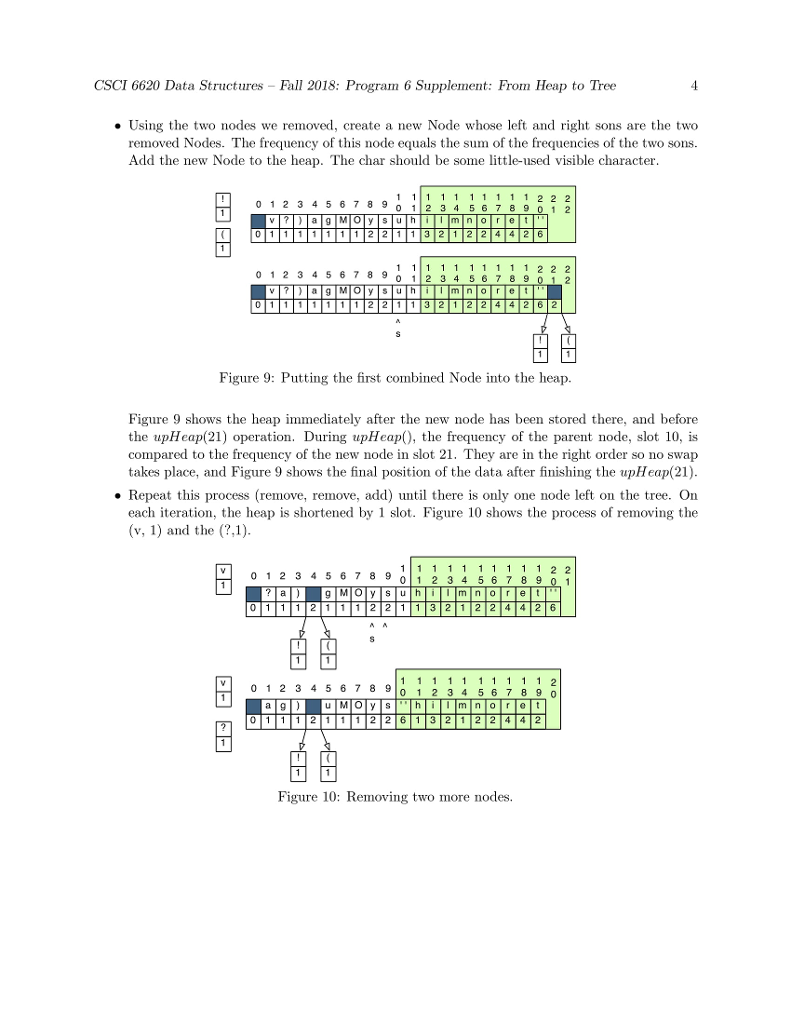
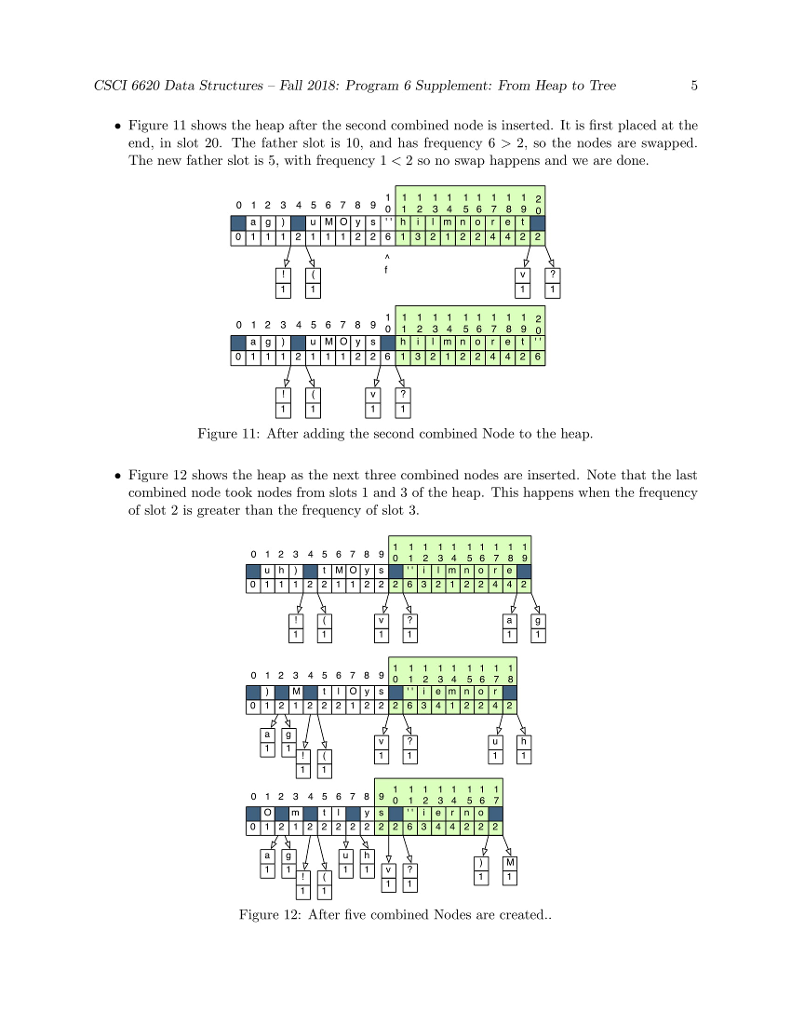
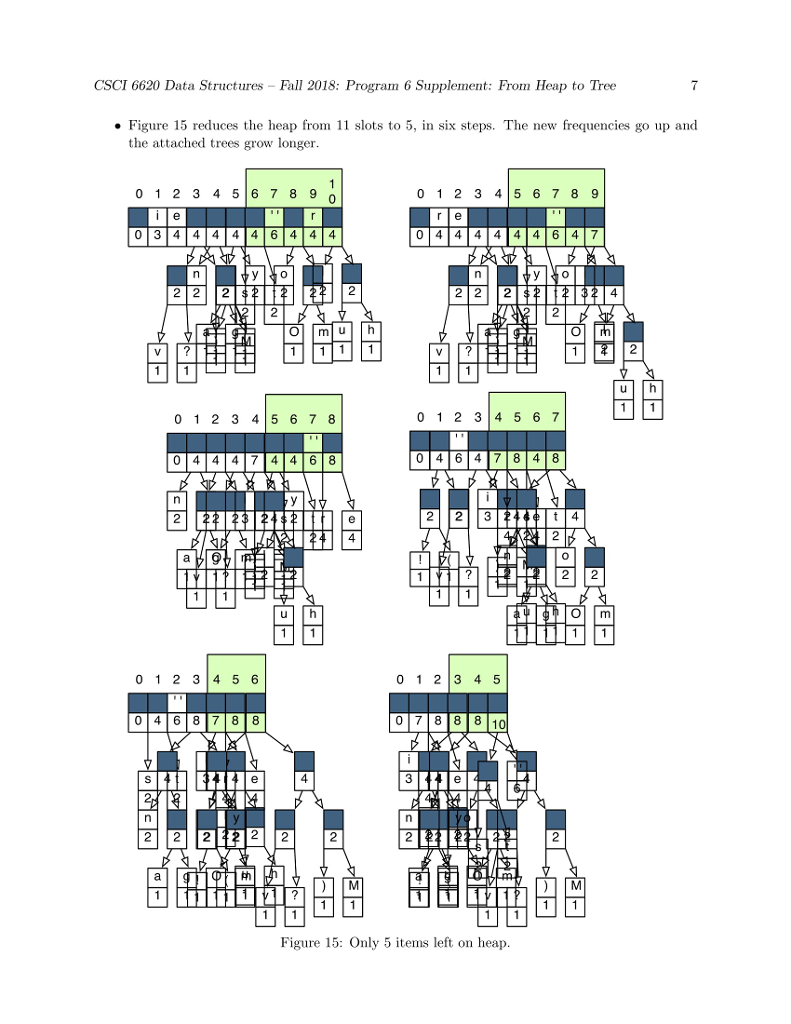
huffman code to compress a file: heap and node 1. to create MAIN,,HUFFMAN(CONTROLLER), INT[]-TALLY TABLE, HUFFFMAN-HP, IFSTREAM-PLAIN TEXT AND HUFF HEAP.. huffman code uses all 8 bits in a byte. 2. Using several major data structures and produce a bit-oriented output file. 3. GOALS OF THE PROGRAM-1. To use a command-line argument for main(), the name of the file to be compressed. 2. To write the first two phases of a file compression program that we be further developed in programs 6 and 7. 3. To use characters as subscripts for an array. 4. To implement / adapt the heap algorithms. The main Program The main program. In main(): 1. Call banner() 2. Then pick up the name of the input file from the command line. Call the Huffman constructor with this file name as its parameter. 3. Call Huffman::compress(). 4. Call bye() and end execution. P5 Phase 1: The Initial Tally In this phase, you will count the number of times each character appears in a text file. Debug this before you start Phase 2. Huffman, the Controller Class. Declare a class named Huffman. It will be instantiated by main and will, in turn, instantiate and run all other parts of the application. Data members for P5 are: 1. tally, an array of 256 integers for counting occurrences of the 256 possible ASCII characters. 2. An ifstream for the input file. 3. A counter for the number of input characters Function members for this phase include: 1. A constructor with one string parameter. Open and verify the file named by the parameter. 2. A print function that prints the final contents of the tally array and the number of characters in the file. This function is for debugging. It is not part of the compression algorithm. Code will be added to this function in later assignments. 3. A private worker function named doTally(). (a) Read the input file one character at a time, in a way that does not skip whitespace. (b) Use the character code to subscript the tally array, and add 1 to the appropriate array slot. (c) When eof is found, make your input file so that it is ready to read again by seeking to 0 bytes from the beginning of the file: streamName.seekg (0, is.beg); 4. A public worker function named compress. This is the primary function that implements the application. It will be called from main and it calls all other major functions. At this time implement the following: (a) Call doTally(). When it returns, print the results of the tally, including the number of characters in the input file. (b) Call the Heap constructor with a pointer to the tally array as its parameter. (c) Call heapify(); it must return a Node* (alias Tree) that is the root of a HuffTree. (d) When heapify() returns, call Heap::print(). (e) Calls on other phases of the program will be added here, as the project develops. Phase 2: The HuffHeap The Node Class This is a helper class for both the HuffHeap class and the HuffTree class. It has four data members. Two (a frequency and a character) will be used by the Heap class. The other two are Node pointers. All four data members will be used by the Tree class. Because this class will be used by two other classes, define it as a fully separate private class that gives friendship to HuffHeap (and later also to HuffTree). At the top of the Node class, write a typedef that makes the name Tree a synonym for Node* 1. Define a private Node constructor with two parameters, the character and its frequency. Use the parameters to initialize two data members. Set the other two to nullptr. In P6, you will define another constructor with different parameters. 2. Define a private print function that prints the char first,followed by a space, followed by the frequency. If a char is invisible, print the ascii code instead. The HuffHeap Class The Heap class will make a min-heap out of the tallies created in Phase 1. Data members. 1. An empty array of 257 Trees. 256 is the maximum possible number of tallies, and slot 0 of this array will always be left empty. 2. An integer subscript of the last array slot that is in use. This is also the number of tally objects in the array. Set this initially to 0. The first Node should go in slot 1. 3. Integers for use by the heap algorithms: the subscripts of father, leftSon, and rightSon. Public function members. 1. A public constructor with one parameter, the int[] tally array. This will be called from the Huffman class. Use the parameter to access the array in the Huffman class. Walk through the array, looking for non-zero counters. If you find one, construct a new Node and store the pointer in the next open slot in the Heap array. 2. A public print function. Output the number of Trees in the heap and then print all of them (use delegation). 3. A public worker function named heapify() or buildHeap(). Implement the buildHeap algorithm from the notes. In the process, implement private functions for upHheap() and downHheap(). Note; the rest of the Heap functions will be added in Program 6. Now look at Figure 1. This array is not in heap order. For example, the path from the root to the node at subscript 21 goes through nodes 1, 2, 5, 10, and 21. This path is not sorted because node 5 has a higher frequency than node 10. To make this into a legal min-heap, we execute the heapify() operation. Refer to the separate Heapify handout for detailed descriptions of the functions and a trace of the heapify algorithm.

INPUT FILE:

input text :

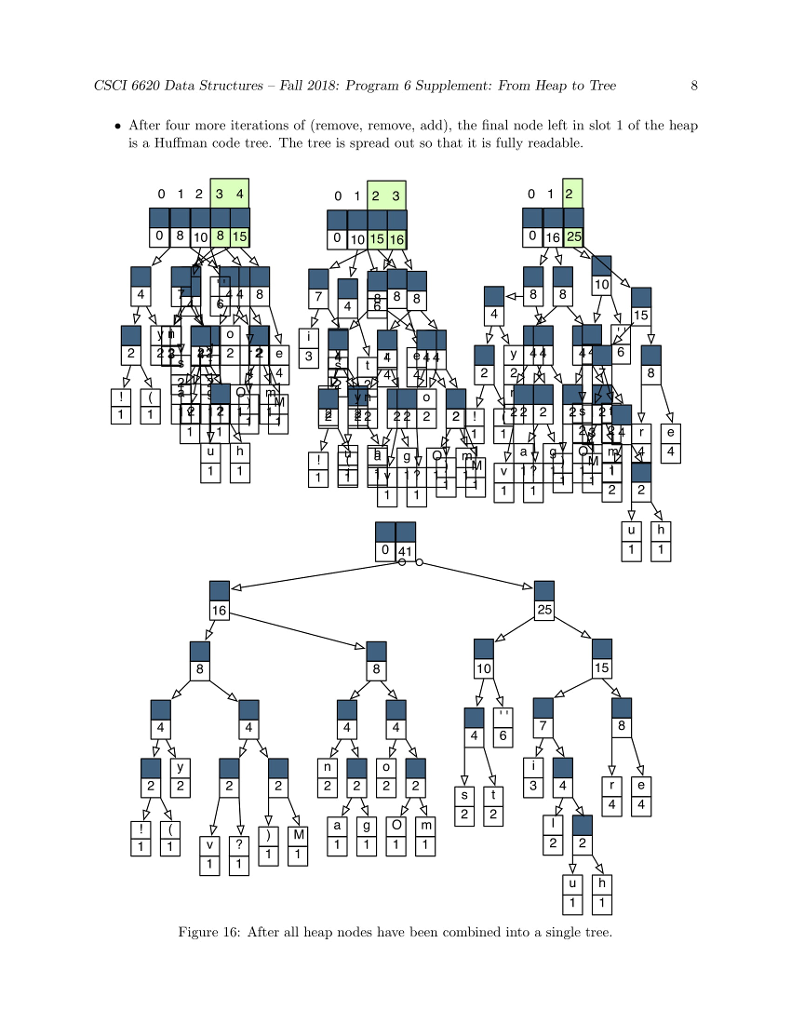
aaaa bbc aaaa bbc d eee eee eee fff ggg

CSCI 6620 Data Structures Fall 2018 Program 6 Supplement: From Heap to Tree 1 Building the Heap For each non-zero-count character, make a new Node using the character and its frequency. Put all of the nodes into an array, starting with slot 1. The result for our text will be: 0 1 2 345 6 78 9012 3 4 5 6 7 8 9 01116111 41 1 3 2122 422 1 2 Figure 1: The heap array before heapify) This array is compact (with no holes), as a heap must be, but it is not in heap order. A heap represents a complete binary tree in which every path from the root of the tree to a leaf is in sorted order. The root is stored in subscript 1 and the sons of any node n are in subscripts 2n and 2n +1 Now look at Figure 1. This array is not in heap order. For example, the path from the root to the node at subscript 21 goes through nodes 1, 2, 5, 10, and 21. This path is not sorted because node 5 has a higher frequency than node 10. To turn this into a legal min-heap, we exe- cute the heapi fy) operation. Figures 2 through 5 trace the operation of the algorithm on this data. 0 12 3 456 7 8 9 02 3 4 56 7 8 9 01 1 11 611 1 4 1 12 2 42 2 112 Figure 2: The first step of heapify() 0 1 2 3 4 5 678 9 a e 01111 611 1 4 0 12 3 4 5 6 7 8 9 13 21 2 2 4 2 2 1 1 2 9 Figure 3: The second step of heapify) o 1 2 3 4 5678 9 01 2 3 4 5 6 7 8 9 0111161 11 113 212 2 42 2 1 1 2 Figure 4: DownHeap(9) When k-8,7, and 6, the DownHeap algorithm exits immediately because the frequency in these slots is 1. The next real work happens when k-5 CSCI 6620 Data Structures Fall 2018 Program 6 Supplement: From Heap to Tree 1 Building the Heap For each non-zero-count character, make a new Node using the character and its frequency. Put all of the nodes into an array, starting with slot 1. The result for our text will be: 0 1 2 345 6 78 9012 3 4 5 6 7 8 9 01116111 41 1 3 2122 422 1 2 Figure 1: The heap array before heapify) This array is compact (with no holes), as a heap must be, but it is not in heap order. A heap represents a complete binary tree in which every path from the root of the tree to a leaf is in sorted order. The root is stored in subscript 1 and the sons of any node n are in subscripts 2n and 2n +1 Now look at Figure 1. This array is not in heap order. For example, the path from the root to the node at subscript 21 goes through nodes 1, 2, 5, 10, and 21. This path is not sorted because node 5 has a higher frequency than node 10. To turn this into a legal min-heap, we exe- cute the heapi fy) operation. Figures 2 through 5 trace the operation of the algorithm on this data. 0 12 3 456 7 8 9 02 3 4 56 7 8 9 01 1 11 611 1 4 1 12 2 42 2 112 Figure 2: The first step of heapify() 0 1 2 3 4 5 678 9 a e 01111 611 1 4 0 12 3 4 5 6 7 8 9 13 21 2 2 4 2 2 1 1 2 9 Figure 3: The second step of heapify) o 1 2 3 4 5678 9 01 2 3 4 5 6 7 8 9 0111161 11 113 212 2 42 2 1 1 2 Figure 4: DownHeap(9) When k-8,7, and 6, the DownHeap algorithm exits immediately because the frequency in these slots is 1. The next real work happens when k-5