Hypothesis Testing

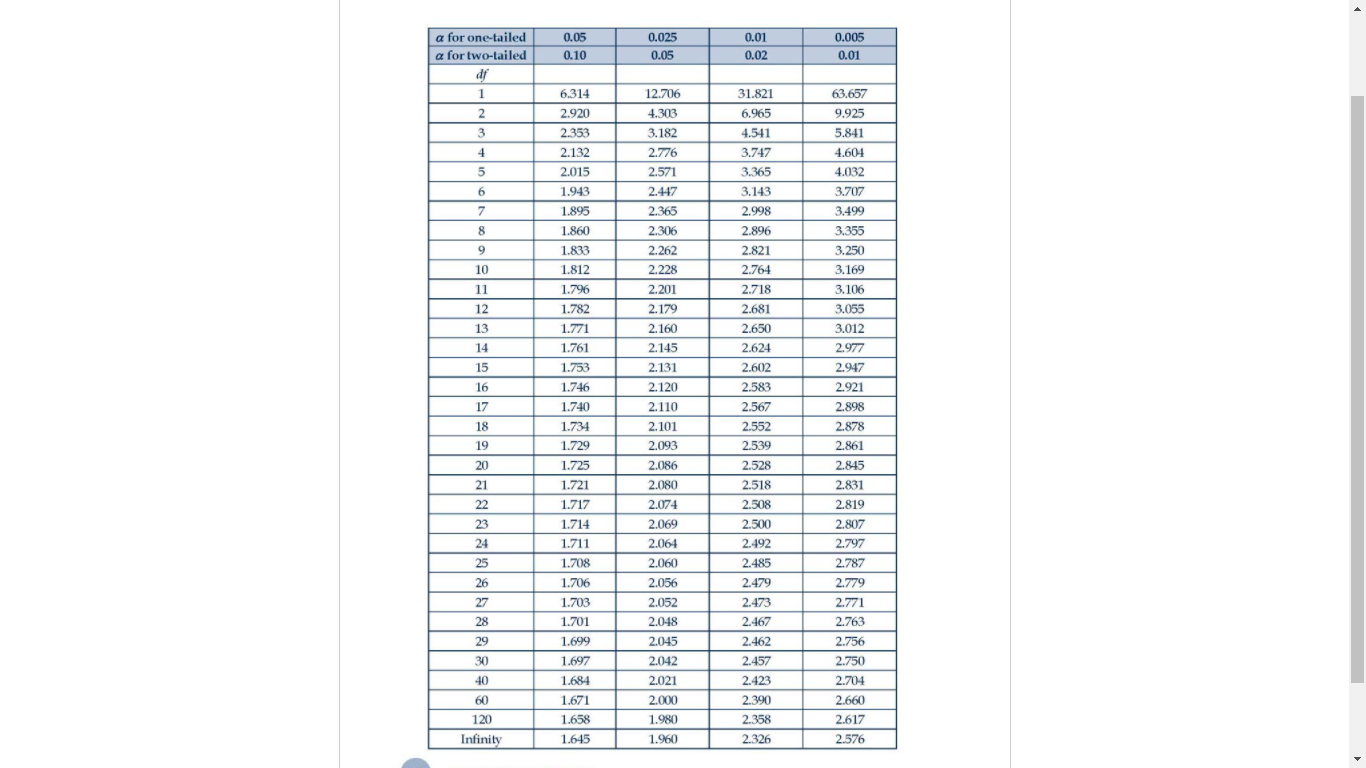
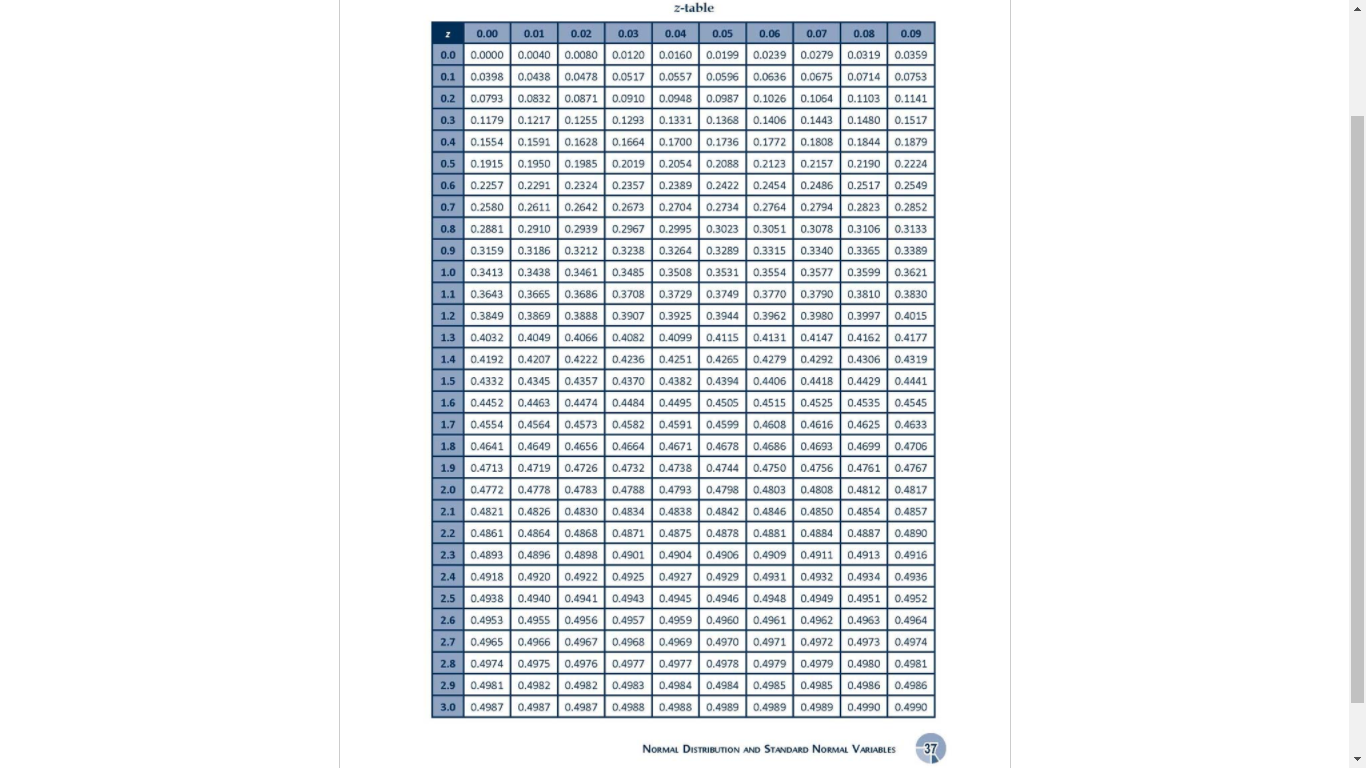
Problem 1. ( This is for question : - 5). The average lifespan of the Americans is recorded to be 70 years with a standard deviation of 8.9 years. A random sample of 100 recorded deaths in the US showed a lifespan of 71.8 years. At o.05 level of significance, test the hypothesis. Your answer 1. What test is appropriate to use ? z - test O t - test 2. What is the computed value? Round-off your answer to three decimal numbers ( Example 1-23+ Your answer 3. What is the critical value? Your answer 4. What is the decision? accept Ho reject Ho 5. What must be the conclusion? The average lifespan of Americans is equal to 70 years. The average lifespan of Americans is not equal to 70 years.problem z. ( This is for question 6-10 ). Records show that the average height of SHS students is 162.5 em. A random sample of 20 SHS students was taken and found to have an average height of 165 em with a standard deviation of 6.9 cm. At on ( two-tailed ) level of significance, is there a reason to believe that the sample is taller than the rest ? Your answer 6. What test is appropriate to use? O z-test O t-test 7. What is the computed value? Round -off to three decimal numbers ( Example 1.234 ) Your answer 8. What is the critical value ? Your answer 9.What is the decision? O accept Ho O reject Ho 10. What must be the conclusion? O There is no significant difference between the heights of the SHS in the population and the heights of the SHS in the sample. O There is a significant difference between the heights of SHS students in the population and the heights of SHS students in the sample.Problem 3. ( This for question 11-15 ). A random sample of & cigarettes of a certain brand has an average nicotine content of 4.2 milligrams and a standard deviation of 1.4 milligrams. The manufacturer of this brand claims that the average nicotine content of its cigarettes does not exceed an average of 35 milligrams. Atoo ( two -tailed ) level of significance. test the hypothesis. Your answer II. What rest is appropriate to use? O z - test O t-test 12. What is the computed value ? Round -off to three decimal numbers ( Example 1.234 ) Your answer 13. What is the critical value ? Your answer 14- What is the decision ? O accept Ho O reject Ho 15. What must be the conclusion? The average nicotine content is equal to 3.5 milligrams The average nicotine content is not equal to 3.5 milligrams Problem 4. ( This is for question 16-20 ). An electrical firm manufactures light bulbs thatProblem 4. ( This is for question 16-20 ). An electrical firm manufactures light bulbs that have a length of life that is approximately normally distributed with a mean of 8oo hours and a standard deviation of go hours. A sample of go bulbs are rested with a mean life of 788 hours . Is it safe to say that the sample has lesser lifespan than the population? Use 0.025 level of significance. Your answer 16. What test is appropriate to use? O z - test O t- test 17. What is the computed value ? Round-off to three decimal numbers ( Example 1.234 ) Your answer 18. What is the critical value ? Your answer 19. What is the decision ? accept Ho O reject Ho 20. What must be the conclusion? The lifespan is equal to 800 hours The lifespan is not equal to 800 hours.Problem 5.( This is for question 21-25 ) . Jackie, a fast food manager claims that the average waiting time for drive -through orders is 3.6 minutes. To rest this claim, Jackie selected a random sample of 29 orders with an average of 3.67 minutes waiting time and a standard deviation of 0.09 minutes. At on5 ( two-tailed ) level of significance, is there a difference on the waiting time between the sample and the population ? Your answer 21. What test is appropriate to use? O z - test t- test 22. What is the compured value ? Round - off to three decimal numbers ( example : 1.234 ) Your answer 23.What is the critical value ? Your answer 24. What is the decision ? accept Ho reject Ho 25. What is the conclusion? O There is no significant difference on the waiting time of the population and the sample () There is a significant difference on the waiting time of the population and the sample