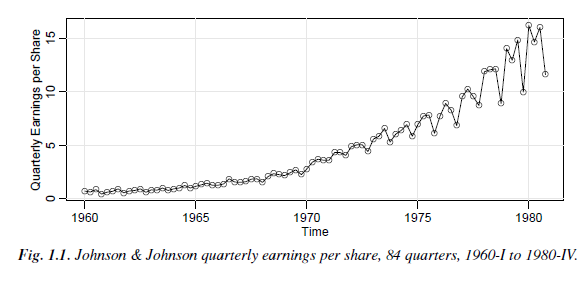
I am having trouble understanding how to do this problem?

2.1 A Structural Model For the Johnson & Johnson data, say yr, shown in Figure 1.1, let x, - log(y). In this problem, we are going to fit a special type of structural model, Ti S, + Nt where T is a trend component, St is a seasonal component, and N is noise. In our case, time t is in quarters (1960.00, 1960.25,...) so one unit of time is a year (a) Fit the regression model trend seasonal noise where Qi(t) = 1 if time t corresponds to quarter i = 1, 2, 3, 4, and zero otherwise The Qi(t)'s are called indicator variables. We will assume for now that wr is a Gaussian white noise sequence. Him: Detailed code is given in Code R.4, the last example of Section R.4 (b) If the model is correct, what is the estimated average annual increase in the logged earnings per share? (c) If the model is correct, does the average logged earnings rate increase or decrease from the third quarter to the fourth quarter? And, by what percentage does it increase or decrease? (d) What happens if you include an intercept term in the model in (a)? Explain why there was a problem. (e) Graph the data, x,, and superimpose the fitted values, say ,, on the graph. s it appear that the Examine the residuals, x, -ir, and state your conclusions. Doe model fits the data well (do the residuals look white)? 2.1 A Structural Model For the Johnson & Johnson data, say yr, shown in Figure 1.1, let x, - log(y). In this problem, we are going to fit a special type of structural model, Ti S, + Nt where T is a trend component, St is a seasonal component, and N is noise. In our case, time t is in quarters (1960.00, 1960.25,...) so one unit of time is a year (a) Fit the regression model trend seasonal noise where Qi(t) = 1 if time t corresponds to quarter i = 1, 2, 3, 4, and zero otherwise The Qi(t)'s are called indicator variables. We will assume for now that wr is a Gaussian white noise sequence. Him: Detailed code is given in Code R.4, the last example of Section R.4 (b) If the model is correct, what is the estimated average annual increase in the logged earnings per share? (c) If the model is correct, does the average logged earnings rate increase or decrease from the third quarter to the fourth quarter? And, by what percentage does it increase or decrease? (d) What happens if you include an intercept term in the model in (a)? Explain why there was a problem. (e) Graph the data, x,, and superimpose the fitted values, say ,, on the graph. s it appear that the Examine the residuals, x, -ir, and state your conclusions. Doe model fits the data well (do the residuals look white)