Question
I am sorry this question may read a little long, but I really need help with this. I will thumb up if I get good
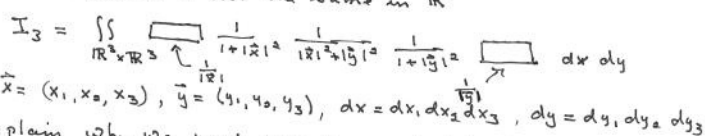
I am sorry this question may read a little long, but I really need help with this.
I will thumb up if I get good answer
In looking at iterated integrals and the role of Fubiui's Theorem we have
?01??01?F(x,y)dxdyand?0???0??F(x)x+y1?f(y)dxdy
eg calculation in the first quadrant where we have to consider both singular behavior at the origin and decay at infinity and for the second integral having f to be a square integrate function which is?0???f(x)?2dx?
We want to explore simple extensions from the product space[0,?][0,?] (in first quadrant) toR2R2 andR3R3
Consider the integral
I2?=??R2R2?1+?x?21???x?2+?y??21??1+?y??21?dxdy
Where x=(x1?,x2?), y?=(y1?,y2?),dx=dx1?dx2?,dy=dy1?dy2?
1.Show that using earlier calculation, we can find the value ofI2?
But the problem is not the same inR3
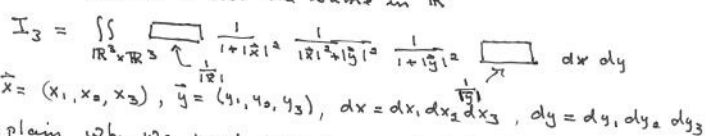
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


