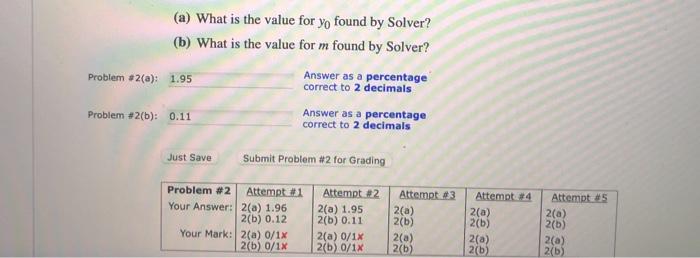
I don't know why my answers are incorrect.
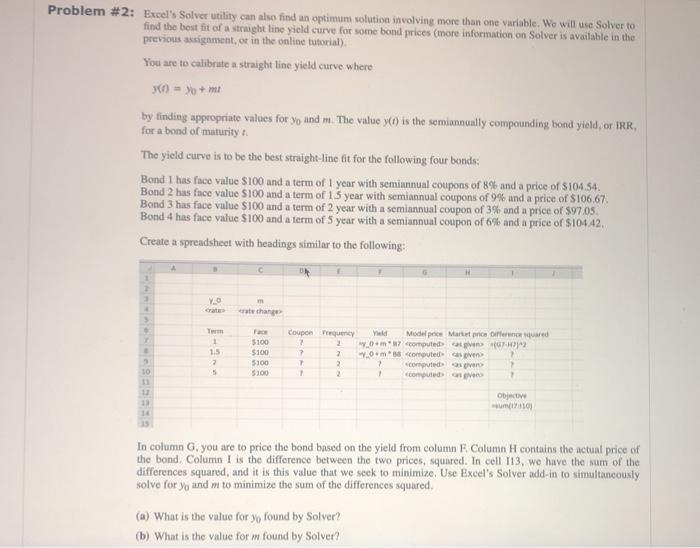
Problem #2: Excel's Solver utility can also find an optimum solution involving more than one variable. We will use Solver to find the best fit of a straight line yield curve for some bond prices (more information on Solver is available in the previous assignment, or in the online tutorial). You are to calibrute a straight line yield curve where by finding appropriate values for yo and m. The value yon is the semiannually compounding bond yield, or IRR for a bond of maturity The yield curve is to be the best straight-line fit for the following four bonds: Bond I has face value $100 and a term of 1 year with semiunnual coupons of 8% and a price of $10454 Bond 2 has face value S100 and a term of 15 year with semiannual coupons of 9% and a price of $106.67. Bond 3 has face value $100 and a term of 2 year with a semiannual coupon of 3% and a price of $97.05. Bond 4 has face value $100 and a term of 5 year with a semiannual coupon of 6% and a price of S104A2. Create a spreadsheet with headings similar to the following: YO 1 1.5 2 5 Face $100 $100 5100 5100 Coupon Frequency 1 2 7 2 2 2 wald Model price Martire quared 0m' computed 67.72 Om computed svens 2 computed computed 10 11 12 14 Obje mum In column G, you are to price the bond based on the yield from column Column H contains the actual price of the bond. Column I is the difference between the two prices, squared. In cell 113, we have the sum of the differences squared, and it is this value that we seek to minimize. Use Excel's Solver add-in to simultaneously solve for yo and m to minimize the sum of the differences squured. (a) What is the value for yo found by Solver? (b) What is the value for m found by Solver? (a) What is the value for yo found by Solver? (b) What is the value for m found by Solver? Answer as a percentage Problem #2(a): 1.95 correct to 2 decimals Answer as a percentage Problem #2(b): 0.11 correct to 2 decimals Just Save Submit Problem #2 for Grading Problem #2 Attempt #1 Your Answer: 2(a) 1.96 2(b) 0.12 Your Mark: 2(a) 0/1x 2(b) 0/1x Attempts 2(a) Attempt #2 2(a) 1.95 2(b) 0.11 2(a) 0/1X 2(b) 0/1x Attempt #3 2(a) 2(b) 2(0 2(b) Attempt 2(a) 2(b) 2(a) 2(b) 2(6) 2(a) 2(b) Problem #2: Excel's Solver utility can also find an optimum solution involving more than one variable. We will use Solver to find the best fit of a straight line yield curve for some bond prices (more information on Solver is available in the previous assignment, or in the online tutorial). You are to calibrute a straight line yield curve where by finding appropriate values for yo and m. The value yon is the semiannually compounding bond yield, or IRR for a bond of maturity The yield curve is to be the best straight-line fit for the following four bonds: Bond I has face value $100 and a term of 1 year with semiunnual coupons of 8% and a price of $10454 Bond 2 has face value S100 and a term of 15 year with semiannual coupons of 9% and a price of $106.67. Bond 3 has face value $100 and a term of 2 year with a semiannual coupon of 3% and a price of $97.05. Bond 4 has face value $100 and a term of 5 year with a semiannual coupon of 6% and a price of S104A2. Create a spreadsheet with headings similar to the following: YO 1 1.5 2 5 Face $100 $100 5100 5100 Coupon Frequency 1 2 7 2 2 2 wald Model price Martire quared 0m' computed 67.72 Om computed svens 2 computed computed 10 11 12 14 Obje mum In column G, you are to price the bond based on the yield from column Column H contains the actual price of the bond. Column I is the difference between the two prices, squared. In cell 113, we have the sum of the differences squared, and it is this value that we seek to minimize. Use Excel's Solver add-in to simultaneously solve for yo and m to minimize the sum of the differences squured. (a) What is the value for yo found by Solver? (b) What is the value for m found by Solver? (a) What is the value for yo found by Solver? (b) What is the value for m found by Solver? Answer as a percentage Problem #2(a): 1.95 correct to 2 decimals Answer as a percentage Problem #2(b): 0.11 correct to 2 decimals Just Save Submit Problem #2 for Grading Problem #2 Attempt #1 Your Answer: 2(a) 1.96 2(b) 0.12 Your Mark: 2(a) 0/1x 2(b) 0/1x Attempts 2(a) Attempt #2 2(a) 1.95 2(b) 0.11 2(a) 0/1X 2(b) 0/1x Attempt #3 2(a) 2(b) 2(0 2(b) Attempt 2(a) 2(b) 2(a) 2(b) 2(6) 2(a) 2(b)