I have a data ( 172, 168, 175, 173, 179, 175 )

And I have three prior distribution of 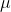, N(169,5) , N(172,5), N(169,10)

How can I make Graph of posterior of these by BernGrid.R code?

BernGrid = function( Theta , pTheta , Data , plotType=c("Points","Bars")[2] ,

showCentTend=c("Mean","Mode","None")[3] ,

showHDI=c(TRUE,FALSE)[2] , HDImass=0.95 ,

showpD=c(TRUE,FALSE)[2] , nToPlot=length(Theta) ) {

# Theta is vector of values between 0 and 1.

# pTheta is prior probability mass at each value of Theta

# Data is vector of 0's and 1's.

# Check for input errors:

if ( any( Theta > 1 | Theta

stop("Theta values must be between 0 and 1")

}

if ( any( pTheta

stop("pTheta values must be non-negative")

}

if ( !isTRUE(all.equal( sum(pTheta) , 1.0 )) ) {

stop("pTheta values must sum to 1.0")

}

if ( !all( Data == 1 | Data == 0 ) ) {

stop("Data values must be 0 or 1")

}

# Create summary values of Data

z = sum( Data ) # number of 1's in Data

N = length( Data )

# Compute the Bernoulli likelihood at each value of Theta:

pDataGivenTheta = Theta^z * (1-Theta)^(N-z)

# Compute the evidence and the posterior via Bayes' rule:

pData = sum( pDataGivenTheta * pTheta )

pThetaGivenData = pDataGivenTheta * pTheta / pData

# Plot the results.

layout( matrix( c( 1,2,3 ) ,nrow=3 ,ncol=1 ,byrow=FALSE ) ) # 3x1 panels

par( mar=c(3,3,1,0) , mgp=c(2,0.7,0) , mai=c(0.5,0.5,0.3,0.1) ) # margins

cexAxis = 1.33

cexLab = 1.75

# convert plotType to notation used by plot:

if ( plotType=="Points" ) { plotType="p" }

if ( plotType=="Bars" ) { plotType="h" }

dotsize = 5 # how big to make the plotted dots

barsize = 5 # how wide to make the bar lines

# If the comb has a zillion teeth, it's too many to plot, so plot only a

# thinned out subset of the teeth.

nteeth = length(Theta)

if ( nteeth > nToPlot ) {

thinIdx = round( seq( 1, nteeth , length=nteeth ) )

} else {

thinIdx = 1:nteeth

}

# Plot the prior.

yLim = c(0,1.1*max(c(pTheta,pThetaGivenData)))

plot( Theta[thinIdx] , pTheta[thinIdx] , type=plotType ,

pch="." , cex=dotsize , lwd=barsize ,

xlim=c(0,1) , ylim=yLim , cex.axis=cexAxis ,

xlab=bquote(theta) , ylab=bquote(p(theta)) , cex.lab=cexLab ,

main="Prior" , cex.main=1.5 , col="skyblue" )

if ( showCentTend != "None" ) {

if ( showCentTend == "Mean" ) {

meanTheta = sum( Theta * pTheta )

if ( meanTheta > .5 ) {

textx = 0 ; textadj = c(0,1)

} else {

textx = 1 ; textadj = c(1,1)

}

text( textx , yLim[2] ,

bquote( "mean=" * .(signif(meanTheta,3)) ) ,

cex=2.0 , adj=textadj )

}

if ( showCentTend == "Mode" ) {

modeTheta = Theta[ which.max( pTheta ) ]

if ( modeTheta > .5 ) {

textx = 0 ; textadj = c(0,1)

} else {

textx = 1 ; textadj = c(1,1)

}

text( textx , yLim[2] ,

bquote( "mode=" * .(signif(modeTheta,3)) ) ,

cex=2.0 , adj=textadj )

}

}

# Mark the highest density interval. HDI points are not thinned in the plot.

if ( showHDI ) {

HDIinfo = HDIofGrid( pTheta , credMass=HDImass )

points( Theta[ HDIinfo$indices ] ,

rep( HDIinfo$height , length( HDIinfo$indices ) ) ,

pch="-" , cex=1.0 )

text( mean( Theta[ HDIinfo$indices ] ) , HDIinfo$height ,

bquote( .(100*signif(HDIinfo$mass,3)) * "% HDI" ) ,

adj=c(0.5,-1.5) , cex=1.5 )

# Mark the left and right ends of the waterline.

# Find indices at ends of sub-intervals:

inLim = HDIinfo$indices[1] # first point

for ( idx in 2:(length(HDIinfo$indices)-1) ) {

if ( ( HDIinfo$indices[idx] != HDIinfo$indices[idx-1]+1 ) | # jumps on left, OR

( HDIinfo$indices[idx] != HDIinfo$indices[idx+1]-1 ) ) { # jumps on right

inLim = c(inLim,HDIinfo$indices[idx]) # include idx

}

}

inLim = c(inLim,HDIinfo$indices[length(HDIinfo$indices)]) # last point

# Mark vertical lines at ends of sub-intervals:

for ( idx in inLim ) {

lines( c(Theta[idx],Theta[idx]) , c(-0.5,HDIinfo$height) , type="l" , lty=2 ,

lwd=1.5 )

text( Theta[idx] , HDIinfo$height , bquote(.(round(Theta[idx],3))) ,

adj=c(0.5,-0.1) , cex=1.2 )

}

}

# Plot the likelihood: p(Data|Theta)

plot( Theta[thinIdx] , pDataGivenTheta[thinIdx] , type=plotType ,

pch="." , cex=dotsize , lwd=barsize ,

xlim=c(0,1) , ylim=c(0,1.1*max(pDataGivenTheta)) , cex.axis=cexAxis ,

xlab=bquote(theta) , ylab=bquote( "p(D|" * theta * ")" ) , cex.lab=cexLab ,

main="Likelihood" , cex.main=1.5 , col="skyblue" )

if ( z > .5*N ) { textx = 0 ; textadj = c(0,1) }

else { textx = 1 ; textadj = c(1,1) }

text( textx ,1.0*max(pDataGivenTheta) ,cex=2.0

,bquote( "Data: z=" * .(z) * ",N=" * .(N) ) ,adj=textadj )

if ( showCentTend != "None" ) {

if ( showCentTend == "Mean" ) {

meanTheta = sum( Theta * pDataGivenTheta )

if ( meanTheta > .5 ) {

textx = 0 ; textadj = c(0,1)

} else {

textx = 1 ; textadj = c(1,1)

}

text( textx , 0.7*max(pDataGivenTheta) ,

bquote( "mean=" * .(signif(meanTheta,3)) ) ,

cex=2.0 , adj=textadj )

}

if ( showCentTend == "Mode" ) {

modeTheta = Theta[ which.max( pDataGivenTheta ) ]

if ( modeTheta > .5 ) {

textx = 0 ; textadj = c(0,1)

} else {

textx = 1 ; textadj = c(1,1)

}

text( textx , 0.7*max(pDataGivenTheta) ,

bquote( "mode=" * .(signif(modeTheta,3)) ) ,

cex=2.0 , adj=textadj )

}

}

# Plot the posterior.

yLim = c(0,1.1*max(c(pTheta,pThetaGivenData)))

plot( Theta[thinIdx] , pThetaGivenData[thinIdx] , type=plotType ,

pch="." , cex=dotsize , lwd=barsize ,

xlim=c(0,1) , ylim=yLim , cex.axis=cexAxis ,

xlab=bquote(theta) , ylab=bquote( "p(" * theta * "|D)" ) , cex.lab=cexLab ,

main="Posterior" , cex.main=1.5 , col="skyblue" )

if ( showCentTend != "None" ) {

if ( showCentTend == "Mean" ) {

meanTheta = sum( Theta * pThetaGivenData )

if ( meanTheta > .5 ) {

textx = 0 ; textadj = c(0,1)

} else {

textx = 1 ; textadj = c(1,1)

}

text( textx , yLim[2] ,

bquote( "mean=" * .(signif(meanTheta,3)) ) ,

cex=2.0 , adj=textadj )

}

if ( showCentTend == "Mode" ) {

modeTheta = Theta[ which.max( pThetaGivenData ) ]

if ( modeTheta > .5 ) {

textx = 0 ; textadj = c(0,1)

} else {

textx = 1 ; textadj = c(1,1)

}

text( textx , yLim[2] ,

bquote( "mode=" * .(signif(modeTheta,3)) ) ,

cex=2.0 , adj=textadj )

}

}

# Plot marginal likelihood pData:

if ( showpD ) {

meanTheta = sum( Theta * pThetaGivenData )

if ( meanTheta > .5 ) {

textx = 0 ; textadj = c(0,1)

} else {

textx = 1 ; textadj = c(1,1)

}

text( textx , 0.75*max(pThetaGivenData) , cex=2.0 ,

bquote( "p(D)=" * .(signif(pData,3)) ) ,adj=textadj )

}

# Mark the highest density interval. HDI points are not thinned in the plot.

if ( showHDI ) {

HDIinfo = HDIofGrid( pThetaGivenData , credMass=HDImass )

points( Theta[ HDIinfo$indices ] ,

rep( HDIinfo$height , length( HDIinfo$indices ) ) ,

pch="-" , cex=1.0 )

text( mean( Theta[ HDIinfo$indices ] ) , HDIinfo$height ,

bquote( .(100*signif(HDIinfo$mass,3)) * "% HDI" ) ,

adj=c(0.5,-1.5) , cex=1.5 )

# Mark the left and right ends of the waterline.

# Find indices at ends of sub-intervals:

inLim = HDIinfo$indices[1] # first point

for ( idx in 2:(length(HDIinfo$indices)-1) ) {

if ( ( HDIinfo$indices[idx] != HDIinfo$indices[idx-1]+1 ) | # jumps on left, OR

( HDIinfo$indices[idx] != HDIinfo$indices[idx+1]-1 ) ) { # jumps on right

inLim = c(inLim,HDIinfo$indices[idx]) # include idx

}

}

inLim = c(inLim,HDIinfo$indices[length(HDIinfo$indices)]) # last point

# Mark vertical lines at ends of sub-intervals:

for ( idx in inLim ) {

lines( c(Theta[idx],Theta[idx]) , c(-0.5,HDIinfo$height) , type="l" , lty=2 ,

lwd=1.5 )

text( Theta[idx] , HDIinfo$height , bquote(.(round(Theta[idx],3))) ,

adj=c(0.5,-0.1) , cex=1.2 )

}

}

return( pThetaGivenData )

} # end of function