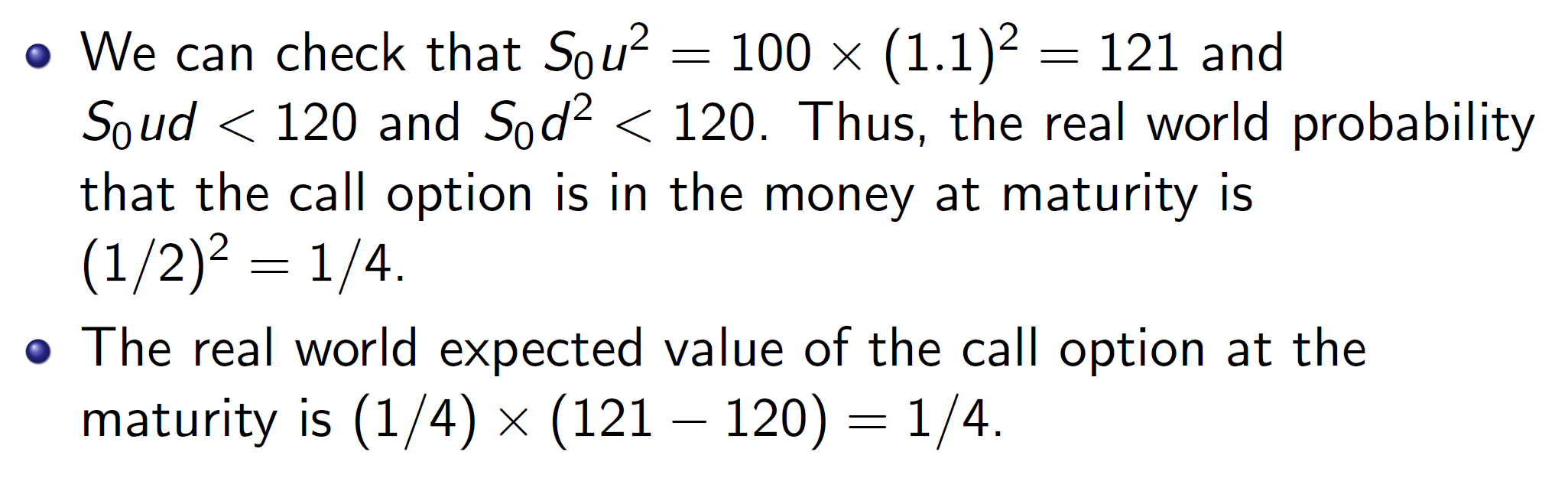I have a very similar question and its answer, hope it helps:
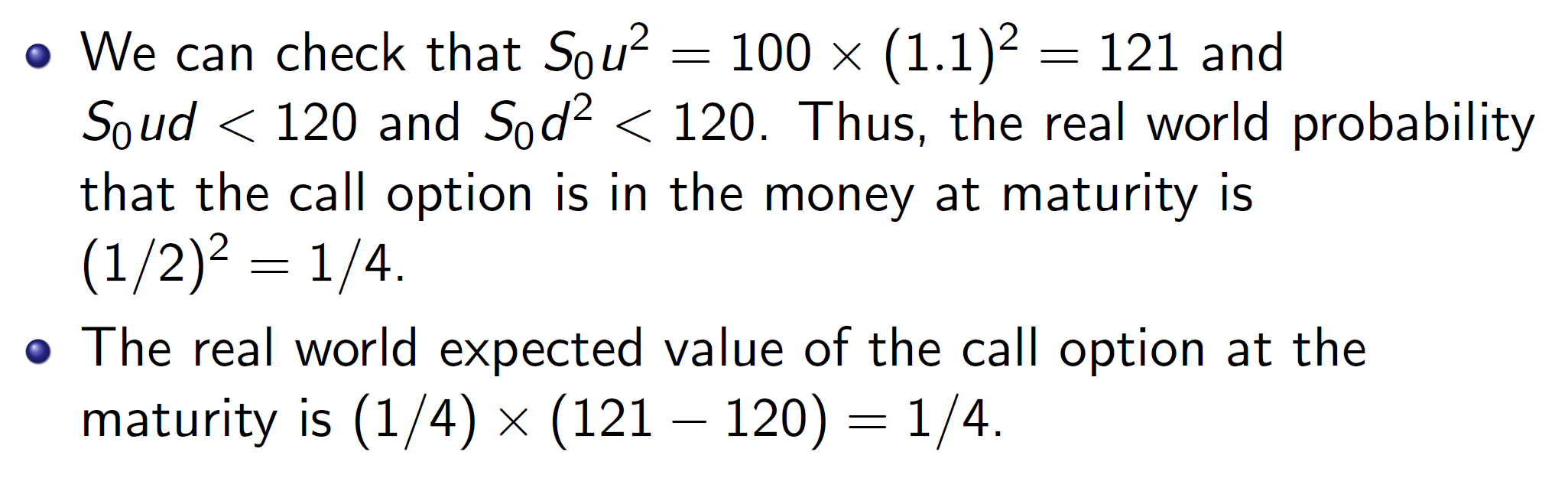
4. (20 points) Consider a non-dividend-paying stock with zero risk-free rate. Assume the stock price follows a binomial tree model with probability of moving up being 1/3 in each period in the real world. Suppose So = 100, u = 1.1 and d = 0.9. For a one-month time step, consider a two-month put option with strike K 120. = 1. What is the real world probability that the put option is in the money at maturity? 2. What is the real world expected value of the put option at the maturity? 3. What is the risk-neutral probability that the put option is in the money at maturity? 4. What is the price of the put option? Consider a non-dividend-paying stock with zero risk-free rate. Assume the stock price follows a binomial tree model with probability of moving up being 1/2 in each period in the real world. Suppose So 100, u = 1.1 and d = 0.8. For a one-month time step, consider a two-month call option with strike K. 120. 0 What is the real world probability that the call option is in the money at maturity? @ What is the real world expected value of the call option at the maturity? * What is the risk-neutral probability that the call option is in the money at maturity? @ What is the price of the call option? We can check that Sou? = 100 (121 120) = 1/4. The risk-neutral probability of price moving up is (1 - d)/(u - d) = 0.2/0.3 = 2/3. . We can check that Sou? = 100 x (1.1)2 = 121 and Soud (121 120) = 4/9. 4. (20 points) Consider a non-dividend-paying stock with zero risk-free rate. Assume the stock price follows a binomial tree model with probability of moving up being 1/3 in each period in the real world. Suppose So = 100, u = 1.1 and d = 0.9. For a one-month time step, consider a two-month put option with strike K 120. = 1. What is the real world probability that the put option is in the money at maturity? 2. What is the real world expected value of the put option at the maturity? 3. What is the risk-neutral probability that the put option is in the money at maturity? 4. What is the price of the put option? Consider a non-dividend-paying stock with zero risk-free rate. Assume the stock price follows a binomial tree model with probability of moving up being 1/2 in each period in the real world. Suppose So 100, u = 1.1 and d = 0.8. For a one-month time step, consider a two-month call option with strike K. 120. 0 What is the real world probability that the call option is in the money at maturity? @ What is the real world expected value of the call option at the maturity? * What is the risk-neutral probability that the call option is in the money at maturity? @ What is the price of the call option? We can check that Sou? = 100 (121 120) = 1/4. The risk-neutral probability of price moving up is (1 - d)/(u - d) = 0.2/0.3 = 2/3. . We can check that Sou? = 100 x (1.1)2 = 121 and Soud (121 120) = 4/9
