i have an exam tomorrow i need help please

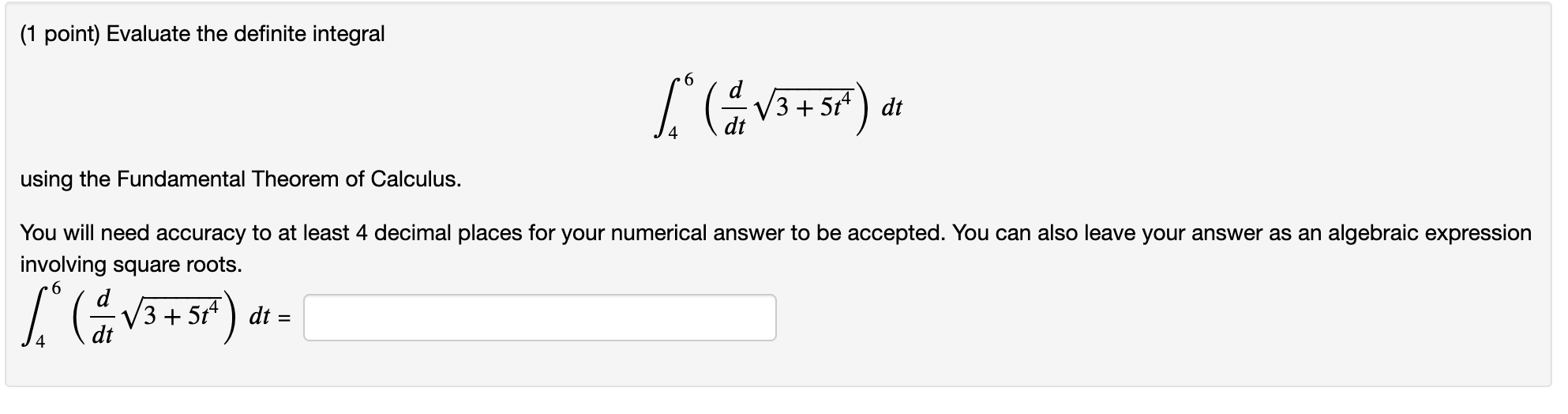
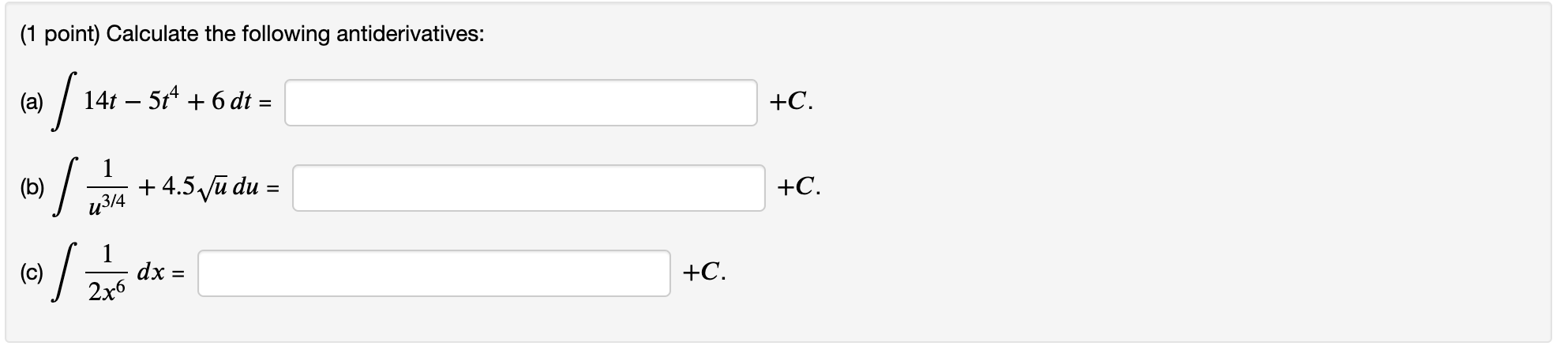
(1 point) Consider the function f(x) = i %. Let F(x) be the antiderivative of f (x) with F(1) = 0. Then F(2) equals -(375/64) (1 point) Evaluate the definite integral using the Fundamental Theorem of Calculus. You will need accuracy to at least 4 decimal places for your numerical answer to be accepted. You can also leave your answer as an algebraic expression involving square roots. ram) dt \f\fd (1 point) Find the most general antiderivative for the function dy = 4ex + 5. x Note: Don't enter the +6 . It's included for you. Antiderivative = + C. \f(1 point) Given that the graph of f passes through the point (1, 1) and that the slope of its tangent line at (x, f(x)) is 2x + 1, find f (-5). m = \f(1 point) Sketch the region between y = 4x 1 and the x-axis over the interval [2, 6]. Find the area of the region. (1 point) Find the area of the region between the curves y = |x| and y = x2 2. Area between curves =