need help with these questions

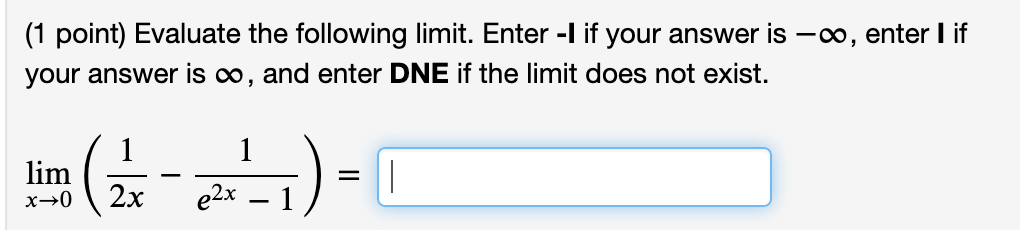
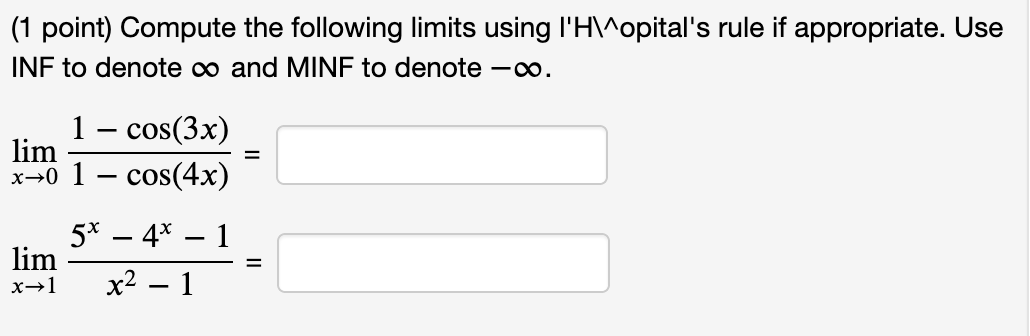
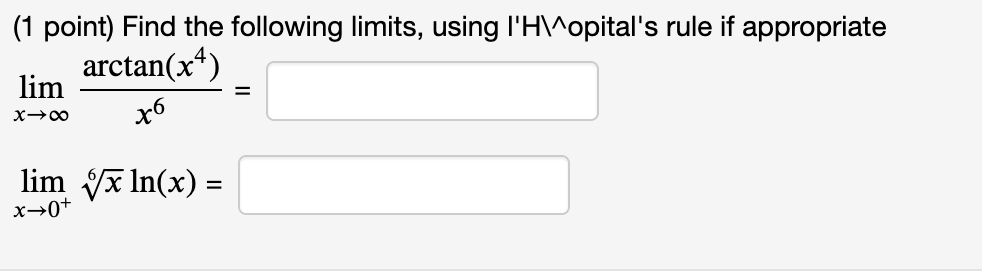
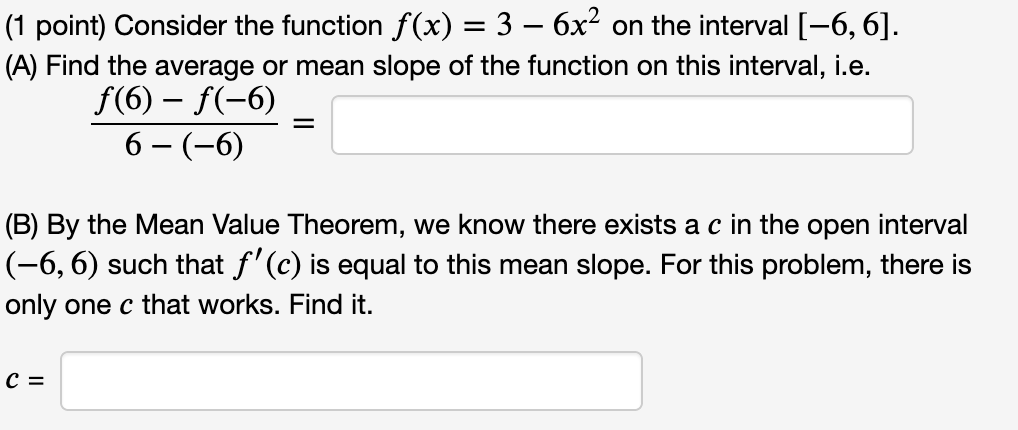
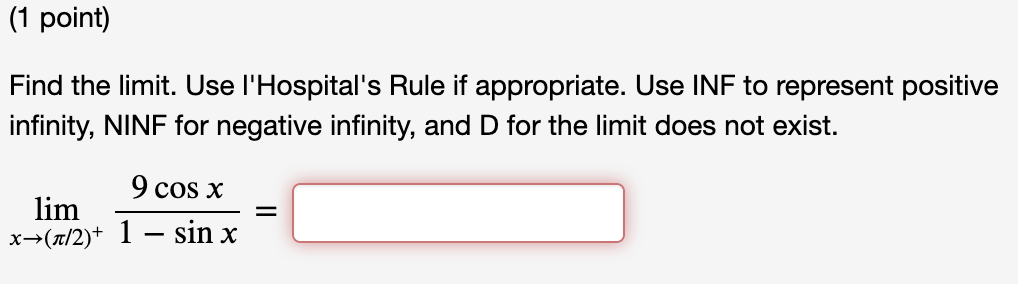
(1 point) Consider the function f (x) = 4x3 5x on the interval [3, 3]. (A) Find the average or mean slope of the function on this interval. Average Slope = 31 (B) By the Mean Value Theorem, we know there exists at least one c in the open interval (3, 3) such that f ' (c) is equal to this mean slope. Find all values of c that work and list them (separated by commas) in the box below. List of values: % on the interval [5, 7]- (A) Find the average or mean slope of the function on this interval. (1 point) Consider the function f (x) = Average Slope = (B) By the Mean Value Theorem, we know there exists a c in the open interval (5, 7) such that f ' (c) is equal to this mean slope. Find all values of c that work and list them (separated by commas) in the box below. List of values: (1 point) Consider the function f (x) = 10)? + 2 on the interval [2, 5]. (A) Find the average or mean slope of the function on this interval. Average Slope = (B) By the Mean Value Theorem, we know there exists at least one c in the open interval (2, 5) such that f ' (c) is equal to this mean slope. Find all values of c that work and list them (separated by commas) in the box below. List of values: (1 point) Consider the function f (x) = 3 6;):2 on the interval [6, 6]. (A) Find the average or mean slope of the function on this interval, i.e. f(6) - f (6) _ 6 (6) (B) By the Mean Value Theorem, we know there exists a c in the open interval (6, 6) such that f ' (c) is equal to this mean slope. For this problem, there is only one c that works. Find it. C: (1 point) Consider the function f (x) = 3 6x2 on the interval [6, 6]. (A) Find the average or mean slope of the function on this interval, i.e. f(6) f(6) _ 6 (6) (B) By the Mean Value Theorem, we know there exists a c in the open interval (6, 6) such that f' (c) is equal to this mean slope. For this problem, there is only one c that works. Find it. C: (1 point) Find the limit. Use I'Hospital's Rule if appropriate. Use INF to represent positive infinity, NINF for negative infinity, and D for the limit does not exist. . 9 cos x hm . = x>(7.':f2)"' 1 3111 x Find the limit. Use I'Hospital's Rule if appropriate. Use INF to represent positive infinity, NINF for negative infinity, and D for the limit does not exist. lim 7x + 7 sin x x-0 2x + 2 cos x =Find the limit. Use I'Hospital's Rule if appropriate. Use INF to represent positive infinity, NINF for negative infinity, and D for the limit does not exist. lim 7x2ex = X- -00(1 point) Evaluate the following limit. Enter -I if your answer is 00, enter I if your answer is co, and enter DNE if the limit does not exist. 1 1 n =:J xI>1(1)(2x 2x_1) (1 point) Compute the following limits using I'H\\^opital's rule if appropriate. Use INF to denote co and MINF to denote -o. lim 1 - cos(3x) x-0 1 - cos(4x) = lim 5x _ 4x - 1 x-1 x2 - 1 =(1 point) Find the following limits, using I'H\\ opital's rule if appropriate lim arctan(x4) = X-+00 x6 lim vx In(x) = x-0+