I have the answers to number 1 and 2 already. I just need assistance with number 3. I attached pictures of the answers for numbers 1 and 2. NPV was used for the calculations.

Case:

Suppose you are a health fitness consultant. Your clients come to you for advice ranging from diet and nutrition to exercise. One of your clients is Dustin Winthrop. He is relatively healthy but has an underlying health condition that puts him in the vulnerable category for COVID-19. He is worried about going back to the gym to workout if Monterey County lifts the shelter-in-place order by May 1. He wants you to help him evaluate two options:

Option A:

Go back to the gym. He is currently paying $130 per month for a gym membership. He assumes that this price will likely remain the same for the next 10 years. If he goes back to the gym, he will make sure to observe social distancing, wear gloves and a face mask, and make sure each equipment that he uses is wiped down and sanitized.

Option B:

Purchase Tonal. A home gym that costs $2,995. He also has to purchase equipment worth $495 and pay for installation (assume this is $350) and taxes (assume the sales tax is 9.5% and will be applied to the total cost). He also has to pay a $49 per month membership fee. He assumes this monthly membership fee will likely remain the same for the next 10 years.

Dustin plans to stay on his workout regimen for the next five to ten years. His opportunity cost, i.e., discount rate is between 2.5% - 5%.

Your job is to make a recommendation about which option will be more cost-effective.

Questions for the case:

1. Which of the following capital budgeting decision criteria will you use to make the recommendation? Please write a justification for that criterions suitability for this analysis.

1. • NPV
   • IRR
   • Payback period

2. Please use the method you selected in Step 1 to calculate the outcome for each of the following scenarios (attach a separate sheet showing your solutions for each scenario)

• • If Dustin keeps working out for the next five years and the discount rate is 2.5%.
  • If Dustin keeps working out for the next five years and the discount rate is 5%.
  • If Dustin keeps working out for the next ten years and the discount rate is 2.5%.
  • If Dustin keeps working out for the next ten years and the discount rate is 5%.

3. Based on your results from step 2, make a recommendation for Dustin if

1. • he keeps working out for the next five years (2-10 sentences)
   • he keeps working out for the next ten years (2-10 sentences)

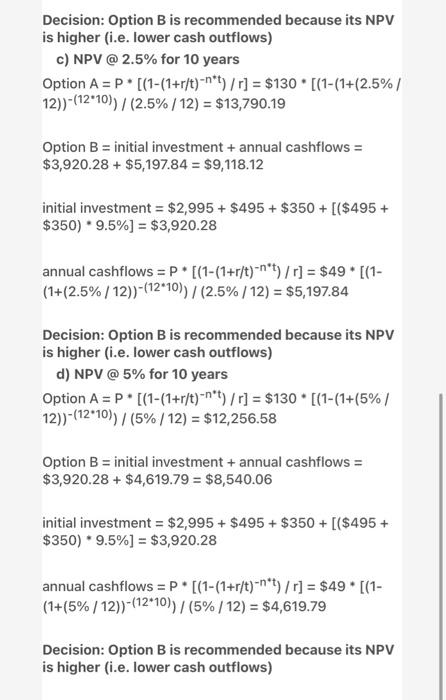
(1) We need to use NPV method, because there will be no cash inflows & IRR & Payback period works only if there would be any positive cash flows. (2) Calculation of NPV: a) NPV @ 2.5% for 5 years Option A =P* [(1-(1+r/t)=*t) /r] = $130 [(1-(1+(2.5% 12))-(1245))/(2.5% / 12) = $7,325.03 Option B = initial investment + annual cashflows = $3,920.28 + $2,760.97 = $6,681.25 initial investment = $2,995 + $495 + $350 + [($495 + $350) * 9.5%] = $3,920.28 annual cashflows =P [(1-(1+r/t)-n*t) /r] = $49. [(1- (1+(2.5% / 12)-(1245))/(2.5% / 12) = $2,760.97 Decision: Option B is recommended because its NPV is higher (i.e. lower cash outflows) b) NPV @ 5% for 5 years Option A =P*[(1-(1+r/t)-nt) /r] = $130 [(1-(1+(5%/ 12))" (1245) / (5% / 12) = $6,888.79 Option B = initial investment + annual cashflows = $3,920.28 + $2,596,.54= $6,516.82 initial investment = $2,995 + $495 + $350 + [($495 + $350) * 9.5%) = $3,920.28 annual cashflows =P [(1-(1+r/t)-n*t) /r] = $49* [(1- (1+(5% / 12)-(125))/(5% / 12) = $2,596,.54 Decision: Option B is recommended because its NPV is higher (i.e. lower cash outflows) Decision: Option B is recommended because its NPV is higher (i.e. lower cash outflows) c) NPV @ 2.5% for 10 years Option A =P [(1-(1+r/t)-n*t) /r] = $130 [(1-(1+(2.5%/ 12))-(1210))/(2.5% / 12) = $13,790.19 Option B = initial investment + annual cashflows = $3,920.28 + $5,197.84 = $9,118.12 initial investment = $2,995 + $495 + $350 + [($495 + $350) 9.5%) = $3,920.28 annual cashflows =P* [(1-(1+r/t)-n't) /r] = $49* [(1- (1+(2.5%/12))+(12-10))/(2.5% / 12) = $5,197.84 Decision: Option Bis recommended because its NPV is higher (i.e. lower cash outflows) d) NPV @ 5% for 10 years Option A =P* [(1-(1+r/t)-n*t) /r] = $130 [(1-(1+(5%/ 12)) - (1210))/(5%/12) = $12,256.58 Option B = initial investment + annual cashflows = $3,920.28 + $4,619.79 = $8,540.06 initial investment = $2,995 + $495 + $350 + [($495 + $350) * 9.5%) = $3,920.28 annual cashflows = P. [(1-(1+r/t)-n*t) /r] = $49. [(1- (1+(5% / 12)-(12*10))/(5% / 12) = $4,619.79 Decision: Option B is recommended because its NPV is higher (i.e. lower cash outflows) (1) We need to use NPV method, because there will be no cash inflows & IRR & Payback period works only if there would be any positive cash flows. (2) Calculation of NPV: a) NPV @ 2.5% for 5 years Option A =P* [(1-(1+r/t)=*t) /r] = $130 [(1-(1+(2.5% 12))-(1245))/(2.5% / 12) = $7,325.03 Option B = initial investment + annual cashflows = $3,920.28 + $2,760.97 = $6,681.25 initial investment = $2,995 + $495 + $350 + [($495 + $350) * 9.5%] = $3,920.28 annual cashflows =P [(1-(1+r/t)-n*t) /r] = $49. [(1- (1+(2.5% / 12)-(1245))/(2.5% / 12) = $2,760.97 Decision: Option B is recommended because its NPV is higher (i.e. lower cash outflows) b) NPV @ 5% for 5 years Option A =P*[(1-(1+r/t)-nt) /r] = $130 [(1-(1+(5%/ 12))" (1245) / (5% / 12) = $6,888.79 Option B = initial investment + annual cashflows = $3,920.28 + $2,596,.54= $6,516.82 initial investment = $2,995 + $495 + $350 + [($495 + $350) * 9.5%) = $3,920.28 annual cashflows =P [(1-(1+r/t)-n*t) /r] = $49* [(1- (1+(5% / 12)-(125))/(5% / 12) = $2,596,.54 Decision: Option B is recommended because its NPV is higher (i.e. lower cash outflows) Decision: Option B is recommended because its NPV is higher (i.e. lower cash outflows) c) NPV @ 2.5% for 10 years Option A =P [(1-(1+r/t)-n*t) /r] = $130 [(1-(1+(2.5%/ 12))-(1210))/(2.5% / 12) = $13,790.19 Option B = initial investment + annual cashflows = $3,920.28 + $5,197.84 = $9,118.12 initial investment = $2,995 + $495 + $350 + [($495 + $350) 9.5%) = $3,920.28 annual cashflows =P* [(1-(1+r/t)-n't) /r] = $49* [(1- (1+(2.5%/12))+(12-10))/(2.5% / 12) = $5,197.84 Decision: Option Bis recommended because its NPV is higher (i.e. lower cash outflows) d) NPV @ 5% for 10 years Option A =P* [(1-(1+r/t)-n*t) /r] = $130 [(1-(1+(5%/ 12)) - (1210))/(5%/12) = $12,256.58 Option B = initial investment + annual cashflows = $3,920.28 + $4,619.79 = $8,540.06 initial investment = $2,995 + $495 + $350 + [($495 + $350) * 9.5%) = $3,920.28 annual cashflows = P. [(1-(1+r/t)-n*t) /r] = $49. [(1- (1+(5% / 12)-(12*10))/(5% / 12) = $4,619.79 Decision: Option B is recommended because its NPV is higher (i.e. lower cash outflows)