I just need the answer for question 6. Thanks.

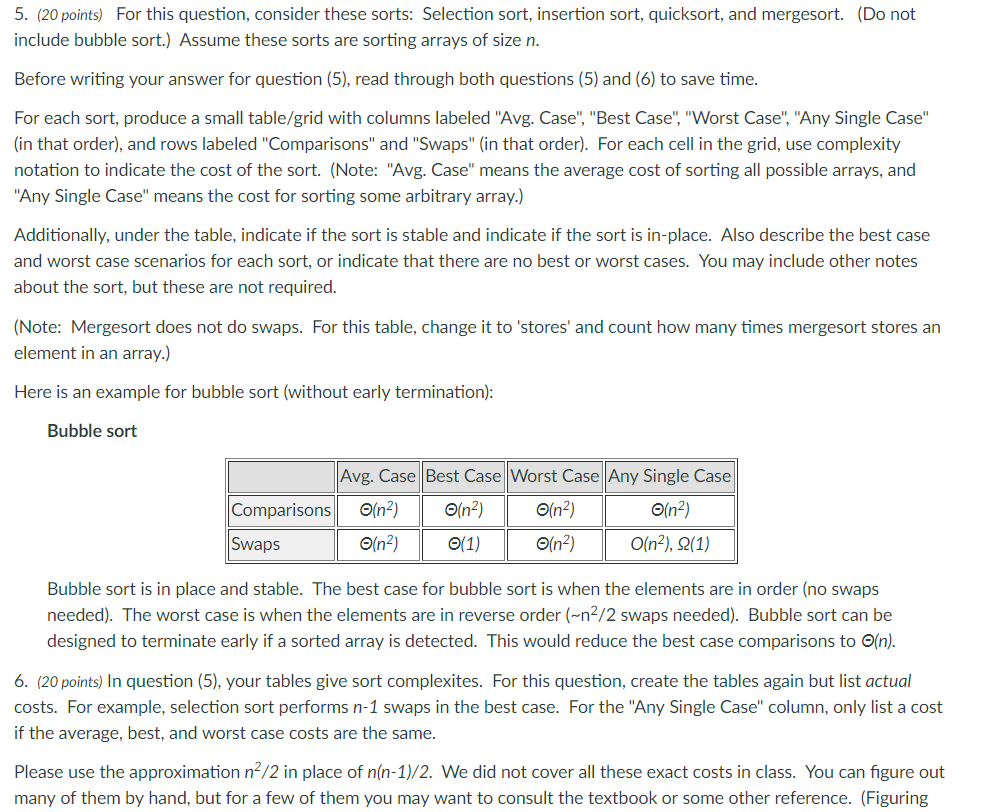
5. (20 points) For this question, consider these sorts: Selection sort, insertion sort, quicksort, and mergesort. (Do not include bubble sort.) Assume these sorts are sorting arrays of size n Before writing your answer for question (5), read through both questions (5) and (6) to save time For each sort, produce a small table/grid with columns labeled "Avg. Case", "Best Case", "Worst Case", "Any Single Case" (in that order), and rows labeled "Comparisons" and "Swaps" (in that order). For each cell in the grid, use complexity notation to indicate the cost of the sort. (Note: "Avg. Case" means the average cost of sorting all possible arrays, and "Any Single Case" means the cost for sorting some arbitrary array.) Additionally, under the table, indicate if the sort is stable and indicate if the sort is in-place. Also describe the best case and worst case scenarios for each sort, or indicate that there are no best or worst cases. You may include other notes about the sort, but these are not required (Note: Mergesort does not do swaps. For this table, change it to 'stores' and count how many times mergesort stores an element in an array.) Here is an example for bubble sort (without early termination) Bubble sort Avg. Case Best Case Worst Case Any Single Case (n2) O(n2) (n2) Comparisons! Swaps (n2) O(n2), (1) ein2) Bubble sort is in place and stable. The best case for bubble sort is when the elements are in order (no swaps needed). The worst case is when the elements are in reverse order (~n2/2 swaps needed). Bubble sort can be designed to terminate early if a sorted array is detected. This would reduce the best case comparisons to (n) 6. (20 points) In question (5), your tables give sort complexites. For this question, create the tables again but list actual costs. For example, selection sort performs n-1 swaps in the best case. For the "Any Single Case" column, only list a cost if the average, best, and worst case costs are the same. Please use the approximation n/2 in place of n(n-1)/2. We did not cover all these exact costs in class. You can figure out many of them by hand, but for a few of them you may want to consult the textbook or some other reference. (Figuring 5. (20 points) For this question, consider these sorts: Selection sort, insertion sort, quicksort, and mergesort. (Do not include bubble sort.) Assume these sorts are sorting arrays of size n Before writing your answer for question (5), read through both questions (5) and (6) to save time For each sort, produce a small table/grid with columns labeled "Avg. Case", "Best Case", "Worst Case", "Any Single Case" (in that order), and rows labeled "Comparisons" and "Swaps" (in that order). For each cell in the grid, use complexity notation to indicate the cost of the sort. (Note: "Avg. Case" means the average cost of sorting all possible arrays, and "Any Single Case" means the cost for sorting some arbitrary array.) Additionally, under the table, indicate if the sort is stable and indicate if the sort is in-place. Also describe the best case and worst case scenarios for each sort, or indicate that there are no best or worst cases. You may include other notes about the sort, but these are not required (Note: Mergesort does not do swaps. For this table, change it to 'stores' and count how many times mergesort stores an element in an array.) Here is an example for bubble sort (without early termination) Bubble sort Avg. Case Best Case Worst Case Any Single Case (n2) O(n2) (n2) Comparisons! Swaps (n2) O(n2), (1) ein2) Bubble sort is in place and stable. The best case for bubble sort is when the elements are in order (no swaps needed). The worst case is when the elements are in reverse order (~n2/2 swaps needed). Bubble sort can be designed to terminate early if a sorted array is detected. This would reduce the best case comparisons to (n) 6. (20 points) In question (5), your tables give sort complexites. For this question, create the tables again but list actual costs. For example, selection sort performs n-1 swaps in the best case. For the "Any Single Case" column, only list a cost if the average, best, and worst case costs are the same. Please use the approximation n/2 in place of n(n-1)/2. We did not cover all these exact costs in class. You can figure out many of them by hand, but for a few of them you may want to consult the textbook or some other reference. (Figuring