I need help ASAP. This is due in about 1 hour. I just need straightforward answers no explanation, please. In English. thankyou

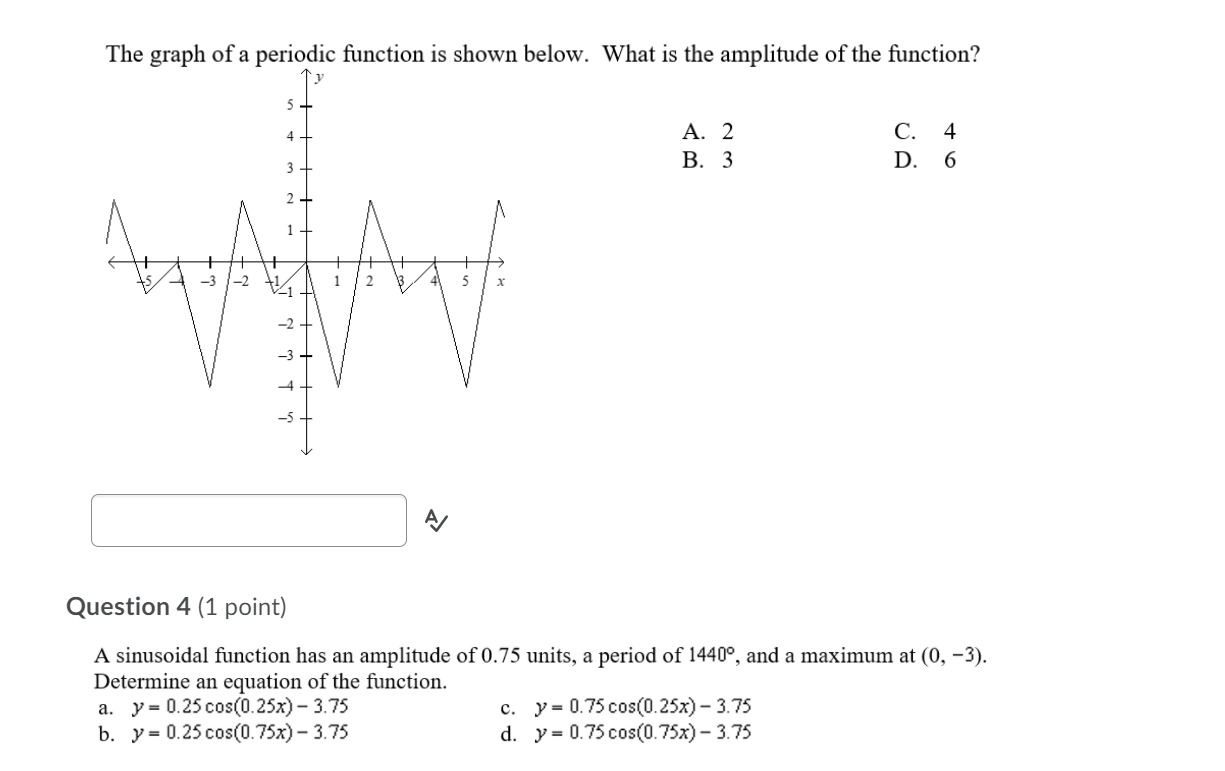
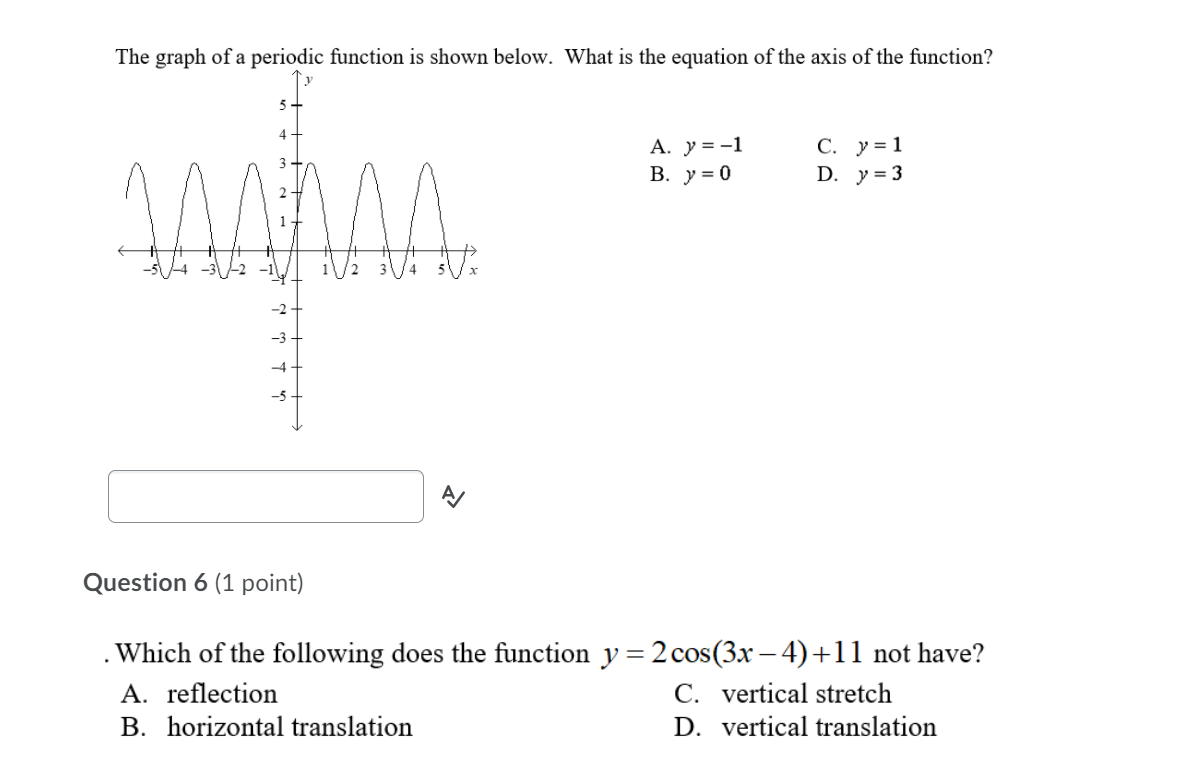
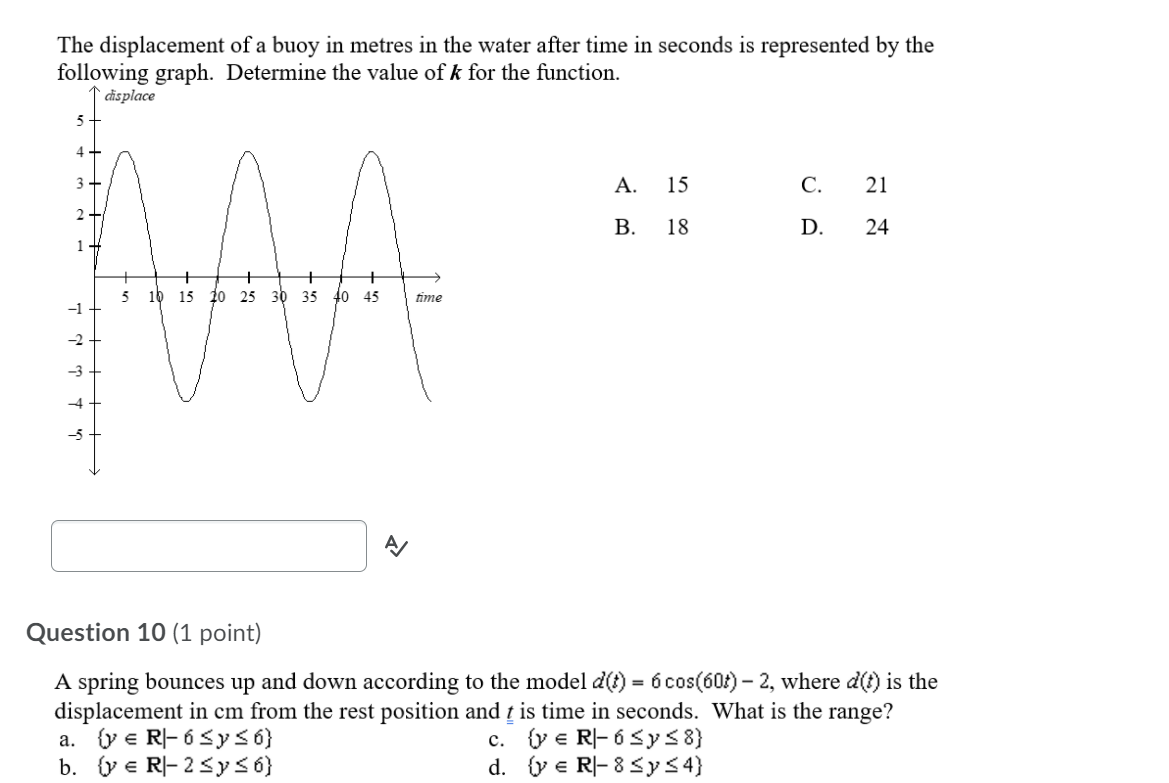
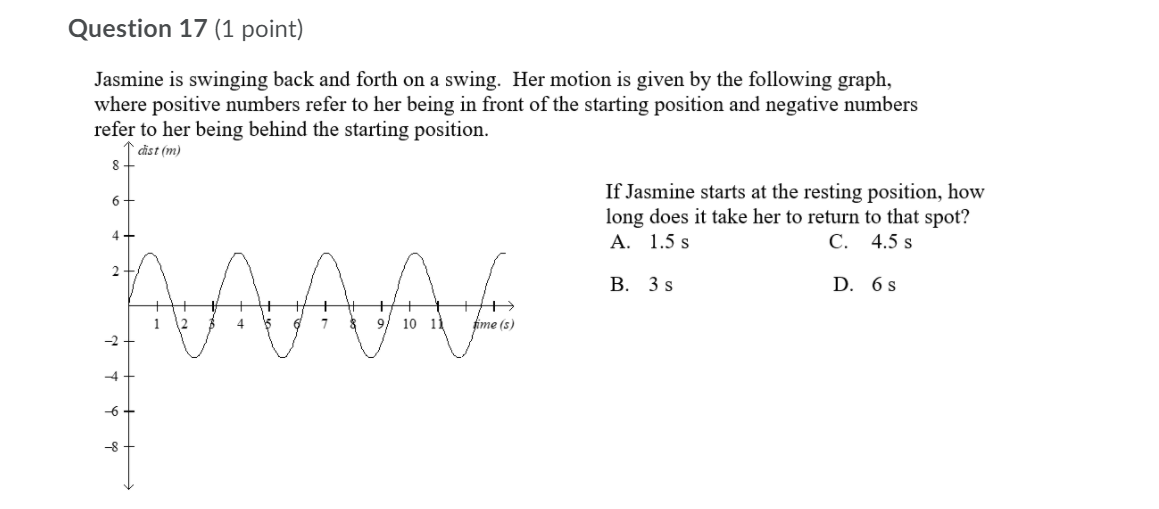
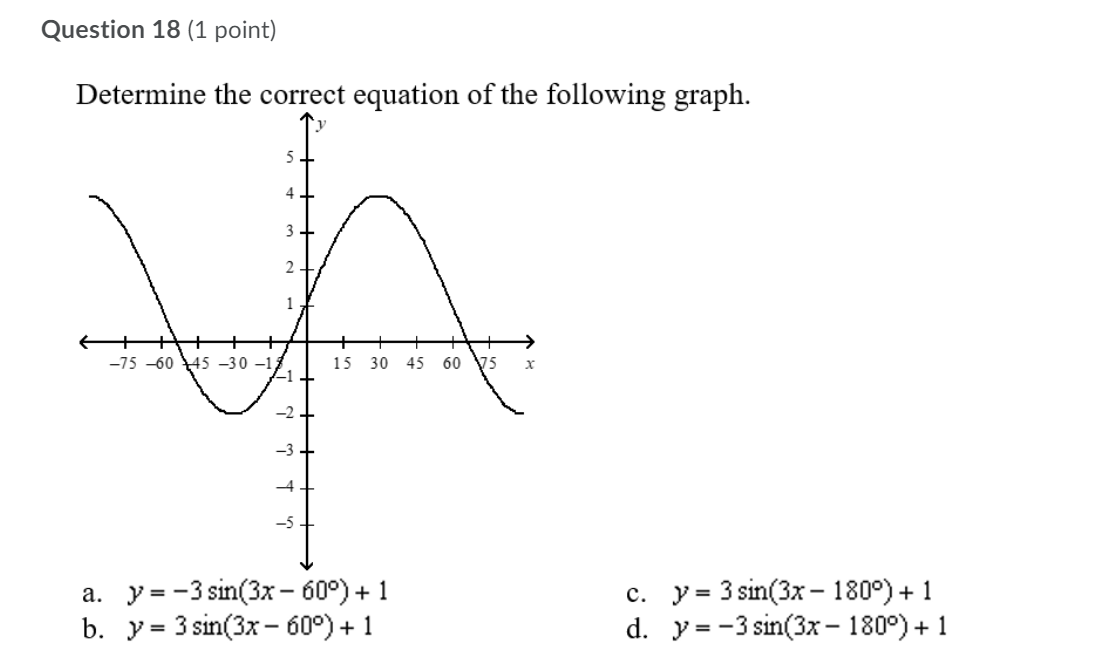
Question 1 (1 point) Which of the following situations would produce a periodic graph? A. passing a basketball, but the hall misses the target and just bounces along the ground B. a machine that cuts a board every 10 s C. a biker's pace through a mountainous terrain D. jumping as high as you can every 10 s for 10 straight minutes \\ l a Question 2 (1 point) If g(x) = sin(6x) + 3 , determine g(15). A. g(15)= 3.71 c. g(15) = 3 B. g(15)=3.87 D. g(lS)=4 The graph of a periodic function is shown below. What is the amplitude of the function? A. 2 C. 4 B. 3 D. 6 2+ 5 x A/ Question 4 (1 point) A sinusoidal function has an amplitude of 0.75 units, a period of 1440, and a maximum at (0, -3). Determine an equation of the function. a. y = 0.25 cos(0.25x) - 3.75 c. y = 0.75 cos(0.25x) - 3.75 b. y = 0.25 cos(0. 75x) - 3.75 d. y = 0.75 cos(0. 75x) - 3.75The graph of a periodic function is shown below. What is the equation of the axis of the function? y .55? 2'4 II 2%: II II cal .50 H w. Question 6 (1 point) .Which of the following does the function y = 2005(3x 4) +11 not have? A. reection C. vertical stretch B. horizontal translation D. vertical translation Question 7 (1 point) The height of a saw tooth in inches after time in seconds is represented by the function y = 0.6 0050 0x + 1.25) 0.4 for r > 0. Without graphing the function, determine the minimum height that the saw tooth reaches. A. 0.4 B. 0.6 C. 0.8 D. l.0 Question 8 (1 point) Frank is riding a Ferris wheel, where g is time in seconds. Suppose the Ferris wheel is 20 m tall. Let 33(1) = 10 cos(12t) represent the height of Frank in n1 above or below the centre of the Ferris wheel. How long does it take to make two complete cycles on the Ferris wheel? Assume there are no stops. A. 60 s C. 45 s B. 305 D. 1205 Q\" The displacement of a buoy in metres in the water after time in seconds is represented by the following graph. Determine the value of k for the function. A displace A. 15 C. 21 B. 18 D. 24 Question 10 {1 point) A spring bounces up and down according to the model d0) - 6 cos(l5l1t) - 2, where d6) is the displacement in cm from the rest position and g is time in seconds. What is the range? a. {yeRlGSySd} c. {yeRI-SyS8} b_ {yeRl-25y56} d. {yew-85364} Which of the following situations would produce a periodic graph? 3. the height of the wheel for a person riding a bike at a constant rate b. the height of a person who is jumping on a trampoline c. the height of a person riding a stationary bike at a constant rate for 5 minutes d. the height of a plane that is in its decent for landing 6/ Question 12 (1 point) Without graphing, determine the period of the function y = 3.75h1(15x) - Ill. a. 24 c. 30 b. 15 d. 3.7 Question 13 (1 point) Determine the equation of a sine function that would have a range of {y e Rl S y S 9} and a period of 60. 3. y- 35in(12x)+ 6 c. y- 1.5 sin(x)+?.5 b. y=3sin(12x)+9 d. y=sin(6x)+9 Question 14 (1 point) If n(x) = cos(4x) - 5, determine n(150). a. n(150) = -5.5 C. #(150) =-4.5 b. #(150) = 5.5 d. 2(150) = 4.5 Question 15 (1 point) Which of the following does the function y = -4 cos(3x) - 9 not have? a. reflection c. vertical translation b. horizontal translation d. horizontal compression AQuestion 16 (1 point) A sinusoidal function has an amplitude of 1.3 units, a period of 1800, and a maximum at (0, 0). Determine an equation of the function. A. C. y = COS -1.3 y = 1.3 cos -1.3 B. D. y = 1.3 cos + 1.3 y =1.3cos UilyQuestion 17 (1 point) Jasmine is swinging back and forth on a swing. Her motion is given by the following graph, where positive numbers refer to her being in front of the starting position and negative numbers refer to her being behind the starting position. A 6:: (ml 6 __ If Jasmine starts at the resting position, how long does it take her to return to that spot? A. 1.5 s C. 4.5 s B. 35 D. 6s 'me (5} Question 18 (1 point) Determine the correct equation of the following graph. + 3 2 -75 -60 145 -30 -17 15 30 45 60 175 a. y = -3 sin(3x - 609) + 1 c. y = 3 sin(3x - 1809) + 1 b. y = 3 sin(3x - 609) + 1 d. y = -3 sin(3x - 1809) + 1