I need help completing a C program.

With input redirection, this input file

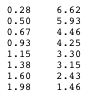
should give an output like this:

urpose The purpose of this assignment is to have you work on a mathematical problem/analysis with single dimensional arrays! functions and multiple files. Scenario When the relationship between two related quantities appears linear, a linear regression equation will give the best fit to that data. The context of this assignment is that you will compute a linear regression equation to fit a straight line to load deflection data for a mechanical coil spring. The computed equation will satisfy the least squares criterion. That is, it will minimize the sum of the from those predicted by the equation. squares of the deviations of the observed deflections We start with a set of experimental data which plots the relationship between two quantities, the weight o:f a load on a spring and the corresponding compression of the spring, Fitting a curve to known data enables estimation of spring deflections for other loads not in the data. This curve can be the basis for calibrating a spring scale. The data consists of a collection of experimentally obtained pairs (x, y) withi - 0, 1, 2, n-1. The x, 's (independent variables) are the weights; the y's (dependent variables) are the corresponding deflections. We want to find a (linear) function fsuch that ffx) fy). A) Least Squares Method The method of least squares, a data pairs, will calculate coefficients m and b in the following linear regression equation: technique used for the equation of a straight line for a set of fc)mx+ b When the original x, values are substitued into the equation, estimate fx) values are obtained. For each x, the residual is defined to be the difference beween the observed y, and the estimated ffxi). The the least squares method is where the sum of the square of the residuals (r) given by: will be minimized. When the sum of squared residuals is computed, we can proceed to compute the correlation between the two related quantities by what is known as the Coefficient of Determination. This is a number typically between 0 and 1 where 1 indicates perfect correlation and 0 is least and numbers in between indicates the measure of correlation. To compute this we also need another number which is called the total sum of squares (t) given by: n- i-0 urpose The purpose of this assignment is to have you work on a mathematical problem/analysis with single dimensional arrays! functions and multiple files. Scenario When the relationship between two related quantities appears linear, a linear regression equation will give the best fit to that data. The context of this assignment is that you will compute a linear regression equation to fit a straight line to load deflection data for a mechanical coil spring. The computed equation will satisfy the least squares criterion. That is, it will minimize the sum of the from those predicted by the equation. squares of the deviations of the observed deflections We start with a set of experimental data which plots the relationship between two quantities, the weight o:f a load on a spring and the corresponding compression of the spring, Fitting a curve to known data enables estimation of spring deflections for other loads not in the data. This curve can be the basis for calibrating a spring scale. The data consists of a collection of experimentally obtained pairs (x, y) withi - 0, 1, 2, n-1. The x, 's (independent variables) are the weights; the y's (dependent variables) are the corresponding deflections. We want to find a (linear) function fsuch that ffx) fy). A) Least Squares Method The method of least squares, a data pairs, will calculate coefficients m and b in the following linear regression equation: technique used for the equation of a straight line for a set of fc)mx+ b When the original x, values are substitued into the equation, estimate fx) values are obtained. For each x, the residual is defined to be the difference beween the observed y, and the estimated ffxi). The the least squares method is where the sum of the square of the residuals (r) given by: will be minimized. When the sum of squared residuals is computed, we can proceed to compute the correlation between the two related quantities by what is known as the Coefficient of Determination. This is a number typically between 0 and 1 where 1 indicates perfect correlation and 0 is least and numbers in between indicates the measure of correlation. To compute this we also need another number which is called the total sum of squares (t) given by: n- i-0