i need help fast!!! these are the question

this is the data

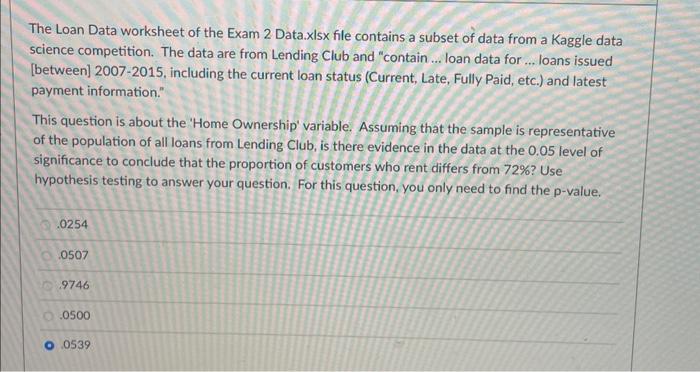
The Loan Data worksheet of the Exam 2 Data.xIsx file contains a subset of data from a Kaggle data science competition. The data are from Lending Club and "contain ... loan data for ... loans issued [between] 2007-2015, including the current loan status (Current, Late, Fully Paid, etc.) and latest payment information." This question is about the 'Home Ownership' variable. Assuming that the sample is representative of the population of all loans from Lending Club, is there evidence in the data at the 0.05 level of significance to conclude that the proportion of customers who rent differs from 72% ? Use hypothesis testing to answer your question. For this question, you only need to find the p-value. \begin{tabular}{|r|} \hline .0254 \\ \hline .0507 \\ \hline .9746 \\ \hline .0500 \\ \hline .0539 \\ \hline \end{tabular} science competition. The data are from Lending Club and "contain ... loan data for ... loans issued [between] 2007-2015, including the current loan status (Current, Late, Fully Paid, etc.) and latest payment information." This question is about the variable "Interest Received," which is the the amount of interest received to date. Suppose that historically the mean interest received for the population from which the sample was taken has been $2,767. Use the appropriate hypothesis test to determine if there is evidence in the data to conclude that the mean value has decreased at the 0.10 level of significance. What is your conclusion? Because the p-value is .8613 , we should not reject the null hypothesis and conclude there is not enough evidence to say that the mean amount of interest received has decreased. Because the p-value is 8613 , we should reject the null hypothesis and conclude there is enough evidence to say that the mean amount of interest received has decreased. Because the p-value is .2774 , we should not reject the null hypothesis and conclude there is not enough evidence to say that the mean amount of interest received has decreased. Because the p-value is 1387 , we should not reject the null hypothesis and conclude there is not enough evidence to say that the mean amount of interest received has decreased. Because the p-value is 2774 , we should reject the null hypothesis and conclude there is enough evidence to say that the mean amount of interest received has decreased. Because the p-value is 1387 , we should reject the null hypothesis and conclude there is enough evidence to say that the mean amount of interest received has decreased. The Loan Data worksheet of the Exam 2 Data.xIsx file contains a subset of data from a Kaggle data science competition. The data are from Lending Club and "contain ... loan data for ... loans issued [between] 2007-2015, including the current loan status (Current, Late, Fully Paid, etc.) and latest payment information." This question is about the 'Home Ownership' variable. Assuming that the sample is representative of the population of all loans from Lending Club, is there evidence in the data at the 0.05 level of significance to conclude that the proportion of customers who rent differs from 72% ? Use hypothesis testing to answer your question. For this question, you only need to find the p-value. \begin{tabular}{|r|} \hline .0254 \\ \hline .0507 \\ \hline .9746 \\ \hline .0500 \\ \hline .0539 \\ \hline \end{tabular} science competition. The data are from Lending Club and "contain ... loan data for ... loans issued [between] 2007-2015, including the current loan status (Current, Late, Fully Paid, etc.) and latest payment information." This question is about the variable "Interest Received," which is the the amount of interest received to date. Suppose that historically the mean interest received for the population from which the sample was taken has been $2,767. Use the appropriate hypothesis test to determine if there is evidence in the data to conclude that the mean value has decreased at the 0.10 level of significance. What is your conclusion? Because the p-value is .8613 , we should not reject the null hypothesis and conclude there is not enough evidence to say that the mean amount of interest received has decreased. Because the p-value is 8613 , we should reject the null hypothesis and conclude there is enough evidence to say that the mean amount of interest received has decreased. Because the p-value is .2774 , we should not reject the null hypothesis and conclude there is not enough evidence to say that the mean amount of interest received has decreased. Because the p-value is 1387 , we should not reject the null hypothesis and conclude there is not enough evidence to say that the mean amount of interest received has decreased. Because the p-value is 2774 , we should reject the null hypothesis and conclude there is enough evidence to say that the mean amount of interest received has decreased. Because the p-value is 1387 , we should reject the null hypothesis and conclude there is enough evidence to say that the mean amount of interest received has decreased