I need help getting a program that would give me the upper and lower bounds of the besselj function with inputs xstart=1, numroot=amount of roots displayed,alpha=0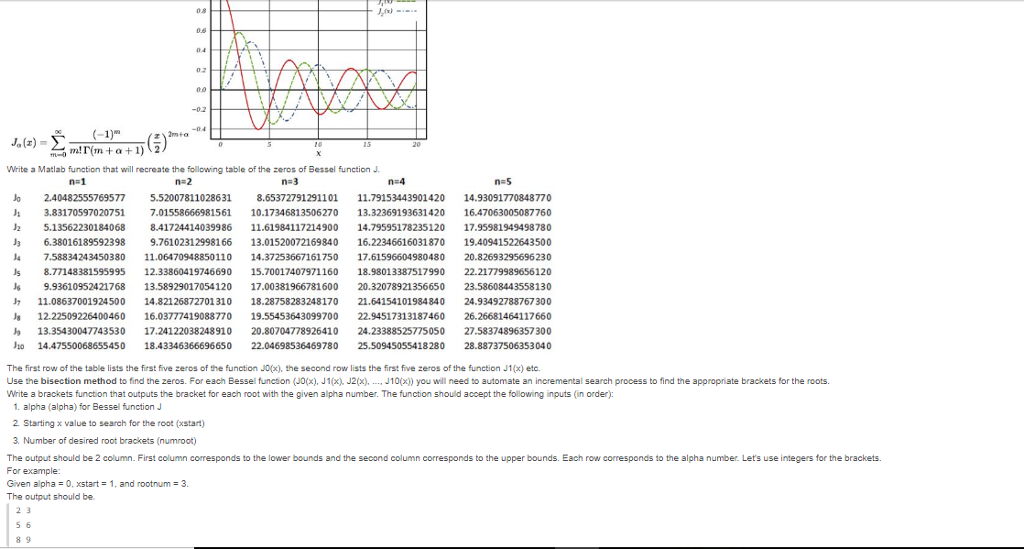
1) J,(z)!(n + + 1) (2) Write a Matlab function that will recreate the following table of the zeros of Bessel function J n-1 n:3 n= 5 Jo 2.40482555769577 5.52007811028631 8.65372791291101 11.79153443901420 14.93091770848770 J 3.831705970207517.01558666981561 10.17346813506270 13.32369193631420 16.47063005087760 2 5.13562230184068 8.41724414039986 11.61984117214900 14.79595178235120 17.95981949498780 J3 6.38016189592398 9.76102312998166 13.01520072169840 16.22346616031870 19.40941522643500 4 7.58834243450380 11.06470948850110 14.37253667161750 17.61596604980430 20.82693295696230 s 8.77148381595995 12.33860419746690 15.70017407971160 18.98013387517990 22.21779989656120 9.93610952421768 13.58929017054120 17.00381966781600 20.32078921356650 23.58608443558130 11.08637001924500 14.82126872701310 18.28758283248170 21.64154101984840 24.93492788767 300 J 12.22509226400460 16.03777419088770 19.55453643099700 22.94517313187460 26.26681464117660 13.35430047743530 17.24122038248910 20.80704778926410 24.23388525775050 27.58374896357300 o 14.47550068655450 18.43346366696650 22.04698536469780 25.50945055418280 28.88737506353040 The first row of the table lists the first five zeros of the function Jopx), the second row lists the first five zeros of the function J1(x) etc. Use the bisection method to find the zeros. For each Bessel function (JO(x), J1x), J2(x), J10x)) you will need to automate an incremental search process to find the appropriate brackets for the roots. Write a brackets function that outputs the bracket for each root with the given alpha number. The function should accept the following inputs (in order) 1. alpha (alpha) for Bessel function J 2. Starting x value to search for the root (xstart) 3. Number of desired root brackets (numroot) The output should be 2 column. First column corresponds to the lower bounds and the second column corresponds to the upper bounds. Each row corresponds to the alpha number. Let's use integers for the brackets For example: Given alpha 0, xstart 1, and rootnum_ 3. The output should be 2 3 5 6 8 9 1) J,(z)!(n + + 1) (2) Write a Matlab function that will recreate the following table of the zeros of Bessel function J n-1 n:3 n= 5 Jo 2.40482555769577 5.52007811028631 8.65372791291101 11.79153443901420 14.93091770848770 J 3.831705970207517.01558666981561 10.17346813506270 13.32369193631420 16.47063005087760 2 5.13562230184068 8.41724414039986 11.61984117214900 14.79595178235120 17.95981949498780 J3 6.38016189592398 9.76102312998166 13.01520072169840 16.22346616031870 19.40941522643500 4 7.58834243450380 11.06470948850110 14.37253667161750 17.61596604980430 20.82693295696230 s 8.77148381595995 12.33860419746690 15.70017407971160 18.98013387517990 22.21779989656120 9.93610952421768 13.58929017054120 17.00381966781600 20.32078921356650 23.58608443558130 11.08637001924500 14.82126872701310 18.28758283248170 21.64154101984840 24.93492788767 300 J 12.22509226400460 16.03777419088770 19.55453643099700 22.94517313187460 26.26681464117660 13.35430047743530 17.24122038248910 20.80704778926410 24.23388525775050 27.58374896357300 o 14.47550068655450 18.43346366696650 22.04698536469780 25.50945055418280 28.88737506353040 The first row of the table lists the first five zeros of the function Jopx), the second row lists the first five zeros of the function J1(x) etc. Use the bisection method to find the zeros. For each Bessel function (JO(x), J1x), J2(x), J10x)) you will need to automate an incremental search process to find the appropriate brackets for the roots. Write a brackets function that outputs the bracket for each root with the given alpha number. The function should accept the following inputs (in order) 1. alpha (alpha) for Bessel function J 2. Starting x value to search for the root (xstart) 3. Number of desired root brackets (numroot) The output should be 2 column. First column corresponds to the lower bounds and the second column corresponds to the upper bounds. Each row corresponds to the alpha number. Let's use integers for the brackets For example: Given alpha 0, xstart 1, and rootnum_ 3. The output should be 2 3 5 6 8 9







