I need help solving this problem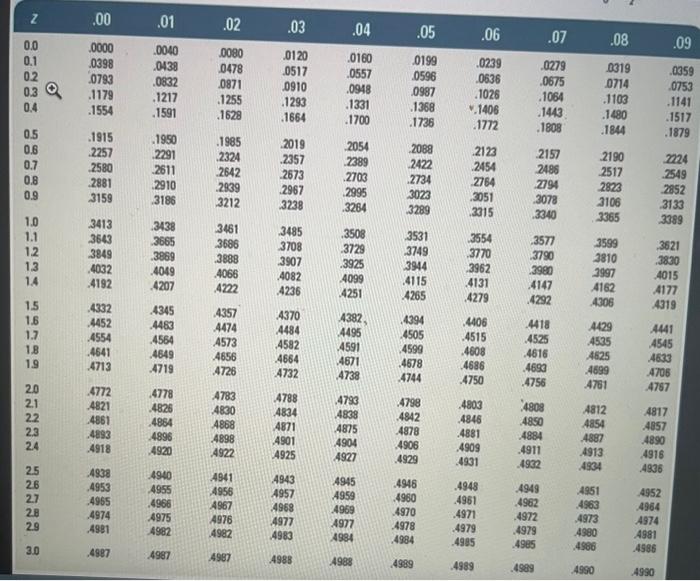

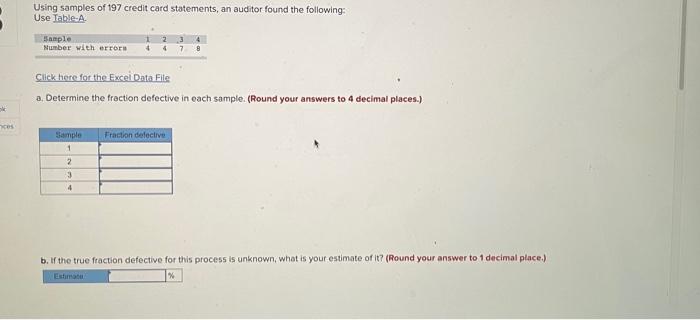
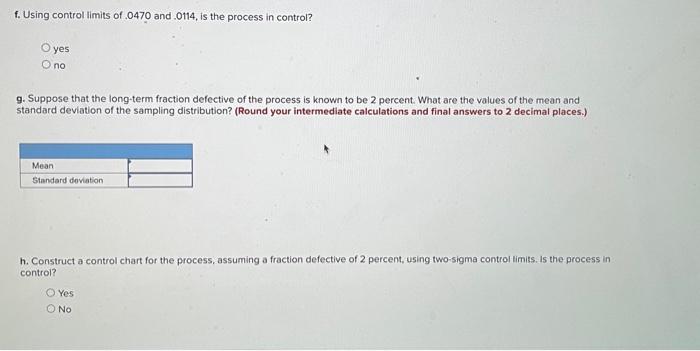
\begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|} \hlinez & .00 & .01 & .02 & .03 & .04 & .05 & .06 & .07 & .08 & .09 \\ \hline 0.0 & .0000 & .0040 & .0080 & .0120 & .0160 & .0199 & .0239 & .0279 & .0319 & .0059 \\ \hline 0.1 & .0398 & .0438 & .0478 & .0517 & .0557 & .0596 & .0636 & .0675 & 0714 & .0753 \\ \hline 02 & .0783 & .0832 & 0871 & .0910 & .0948 & 0987 & .1026 & .1064 & .1103 & .1141 \\ \hline 0.3 & .1179 & .1217 & .1255 & .1293 & .1331 & .1368 & v.1406 & .1443 & .1480 & .1517 \\ \hline 0.4 & .1554 & .1591 & .1628 & .1664 & .1700 & .1736 & 1772 & .1808 & .184 & .1879 \\ \hline 0.5 & .1915 & .1950 & .1985 & 2019 & .2054 & 2088 & .2123 & 2157 & 2190 & m4 \\ \hline 0.8 & .2257 & 2291 & .2324 & .2357 & .2389 & 2422 & 2454 & 2485 & 2517 & 2549 \\ \hline 0.7 & .2580 & 2611 & .2642 & 2673 & .2703 & .2734 & 2764 & 2794 & 2823 & 2052 \\ \hline 0.8 & .2881 & .2910 & .2839 & 2967 & .2995 & 3023 & .3051 & 3078 & 3106 & .3133 \\ \hline 0.9 & 3159 & .3186 & 3212 & 3238 & .3264 & 3289 & .3215 & .3340 & 3365 & 3389 \\ \hline 1.0 & 3413 & .3438 & 3461 & 3485 & .3508 & 3531 & 3554 & .35n & 3599 & .3621 \\ \hline 1.1 & 3643 & .3665 & 3686 & 3708 & 3728 & 3749 & 3770 & 3790 & 3810 & .3830 \\ \hline 1.2 & 3849 & .3869 & .3888 & 3907 & .3925 & 394 & .3962 & 3900 & 3997 & .4015 \\ \hline 1.3 & .4032 & .4049 & .4066 & .4082 & 4099 & .4115 & .4131 & .4147 & 4162 & 417 \\ \hline 1.4 & .4192 & .4207 & .422 & 4236 & 4251 & 4265 & .4279 & .4292 & 4306 & 4319 \\ \hline 15 & .4332 & .4345 & .4357 & 4370 & 4382 , & .4394 & .4406 & 4418 & 4429 & 4441 \\ \hline 1.6 & .4452 & .4463 & 4474 & 4484 & 4495 & 4505 & .4515 & .4525 & .4535 & .4545 \\ \hline 1.7 & .4554 & .4564 & .4573 & .4582 & 4591 & 4599 & .4608 & .4616 & 4625 & .4633 \\ \hline 1.8 & .4641 & 4649 & .4656 & 4664 & 4671 & .4678 & .4686 & .4690 & .4699 & 4706 \\ \hline 19 & .4713 & .4719 & 4726 & 4732 & .4738 & 4744 & .4750 & .4756 & 4761 & .4757 \\ \hline 20 & & 4778 & A783 & 4788 & .4793 & .4798 & .4803 & 4808 & A812 & 4817 \\ \hline 2.1 & 4821 & .4826 & 4830 & 4834 & .4838 & .4842 & 4846 & 4850 & .4854 & A857 \\ \hline 22 & 4881 & 4864 & 4868 & 4871 & 4875 & 4878 & .4881 & 4884 & 4887 & 4890 \\ \hline 2.3 & .4893 & 4896 & 4898 & 4901 & 4904 & 4906 & .4909 & .4911 & 4913 & 4916 \\ \hline 24 & 4918 & 4920 & A922 & 4925 & 4927 & .4929 & .4931 & 4932 & & A936 \\ \hline 2.5 & 4838 & 4940 & ASA1 & 4943 & 4945 & .4948 & .4943 & .4949 & & A952 \\ \hline 26 & .4953 & 4955 & 4956 & A957 & 4959 & 4960 & 4951 & 4962 & 4563 & 4964 \\ \hline 2.7 & .4965 & .4966 & AS67 & 4968 & 4969 & 4970 & .497 & .4972 & 4973 & A974 \\ \hline 28 & .4974 & 4975 & A976 & 4977 & A97 & 4978 & 4979 & .4979 & 4980 & A981 \\ \hline 29 & A981 & 4962 & 4982 & 4983 & ASBA & 4984 & .4985 & .49e5 & .4986 & 4986 \\ \hline 3.0 & .4987 & 4987 & 4987 & A988 & 4988 & 4989 & .4989 & .4989 & 4950 & A990 \\ \hline \end{tabular} Using samples of 197 credit card statements, an auditor found the following: Use Table-A. Click there for the Excei Data Fite a. Determine the frection defective in each sample. (Round your answers to 4 decimal places.) b. If the true fraction defective for this proces5 is unknown, what is your estimate of it? (Round your answer to 1 decimal place.) c. What is your estimate of the mean and standard deviation of the sampling distribution of fractions defective for samples of this size? (Round your intermediate calculations and final answers to 4 decimal places.) d. What control limits would give an alpha risk of .03 for this processy (Round your intermediate calculations to 4 decimal places. Round your " z " value to 2 decimal places and other answers to 4 decimal places.) e. What alpha risk would control limits of .0470 and .0114 provide? (Round your intermediate calculations to 4 decimal places. Round your " z " value to 2 decimal places and "alpha risk" value to 4 decimal places.) f. Using control limits of .0470 and .0114 , is the process in control? yes no 9. Suppose that the long-term fraction defective of the process is known to be 2 percent. What are the values of the mean and standard deviation of the sampling distribution? (Round your intermediate calculations and final answers to 2 decimal places.) h. Construct a control chart for the process, assuming a fraction defective of 2 percent, using two-sigma control limits. Is the process in control? Yes No