i need help with questions 16, 17 , and 18. 17 and 18's answers need to be in fractions.

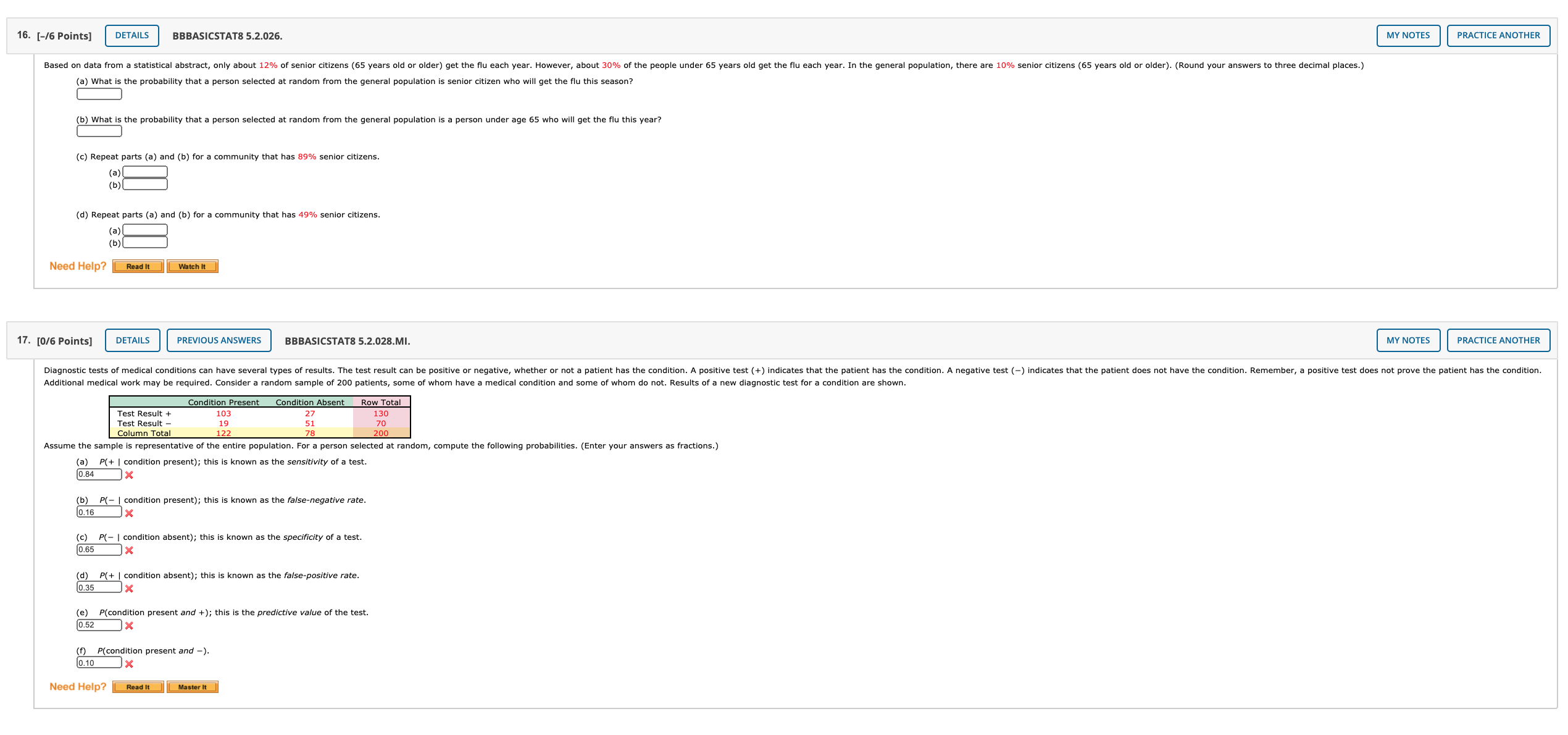
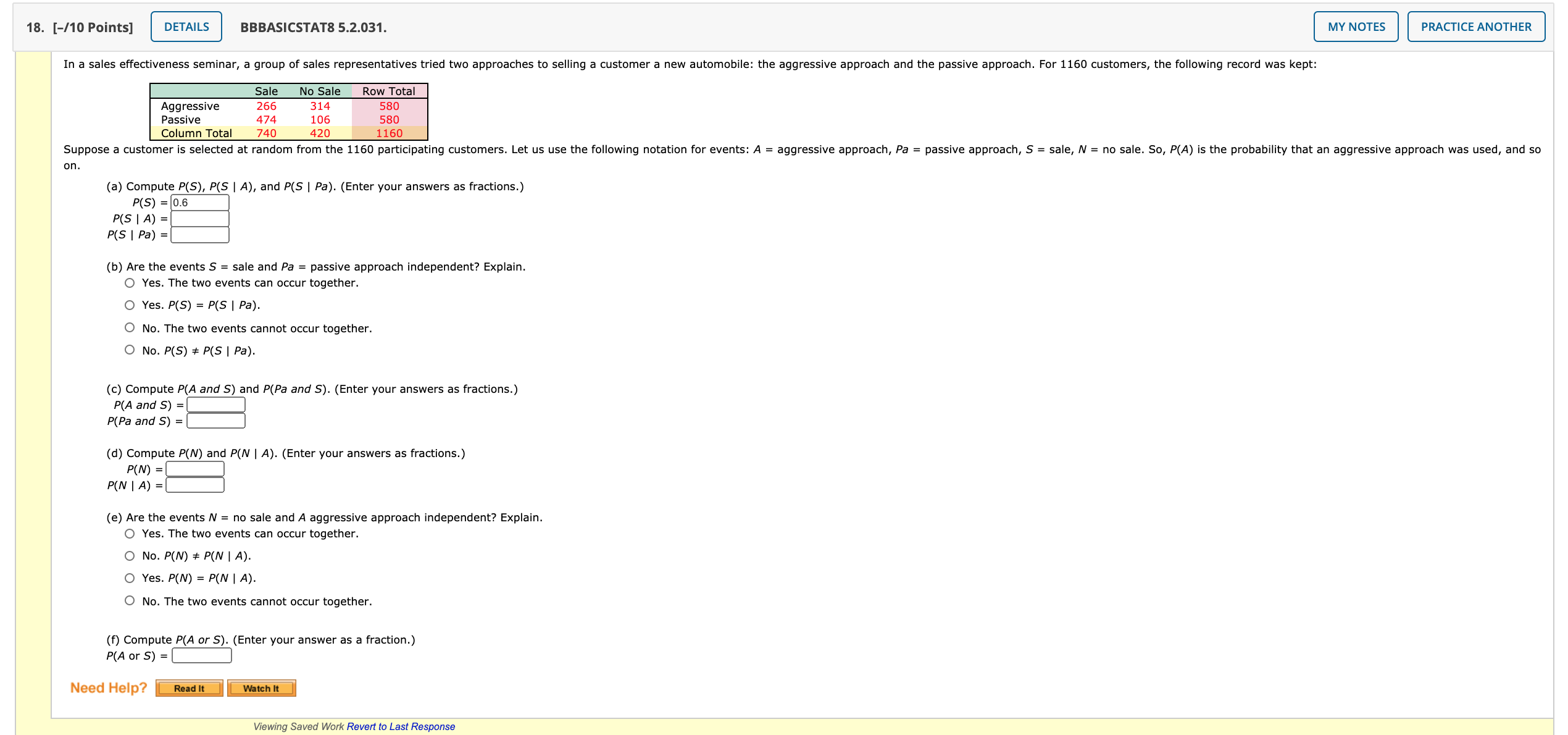
16. [-/6 Points] DETAILS BBBASICSTAT8 5.2.026. MY NOTES PRACTICE ANOTHER Based on data from a statistical abstract, only about 12% of senior citizens (65 years old or older) get the flu each year. However, about 30% of the people under 65 years old get the flu each year. In the general population, there are 10% senior citizens (65 years old or older). (Round your answers to three decimal places.) (a) What is the probability that a person selected at random from the general population is senior citizen who will get the flu this season? b) What is the probability that a person selected at random from the general population is a person under age 65 who will get the flu this year? (c) Repeat parts (a) and (b) for a community that has 89% senior citizens. (a) ( b) ( (d) Repeat parts (a) and (b) for a community that has 49% senior citizens. (a) ( b ) Need Help? Read it Watch It 17. [0/6 Points] DETAILS PREVIOUS ANSWERS BBBASICSTAT8 5.2.028.MI. MY NOTES PRACTICE ANOTHER Diagnostic tests of medical conditions can have several types of results. The test result can be positive or negative, whether or not a patient has the condition. A positive test (+) indicates that the patient has the condition. A negative test (-) indicates that the patient does not have the condition. Remember, a positive test does not prove the patient has the condition. Additional medical work may be required. Consider a random sample of 200 patients, some of whom have a medical condition and some of whom do not. Results of a new diagnostic test for a condition are shown. Condition Present Condition Absent Row Total Test Result + 103 27 130 Test Result - 19 51 70 Column Total 200 Assume the sample is representative of the entire population. For a person selected at random, compute the following probabilities. (Enter your answers as fractions.) (a) P(+ | condition present); this is known as the sensitivity of a test. 0.84 X (b) P(- | condition present); this is known as the false-negative rate. (0.16 (c) P(- | condition absent); this is known as the specificity of a test. 0.65 (d) P(+ | condition absent); this is known as the false-positive rate. 0.35 JX (e) P(condition present and +); this is the predictive value of the test. 0.52 JX f) P(condition present and -). 0.10 JX Need Help? Read it Master It18. [-/10 Points] DETAILS BBBASICSTAT8 5.2.031. MY NOTES PRACTICE ANOTHER In a sales effectiveness seminar, a group of sales representatives tried two approaches to selling a customer a new automobile: the aggressive approach and the passive approach. For 1160 customers, the following record was kept: Sale No Sale Row Total Aggressive 266 314 580 Passive 474 106 580 Column Total 740 420 1160 Suppose a customer is selected at random from the 1160 participating customers. Let us use the following notation for events: A = aggressive approach, Pa = passive approach, S = sale, N = no sale. So, P(A) is the probability that an aggressive approach was used, and so on. (a) Compute P(S), P(S | A), and P(S | Pa). (Enter your answers as fractions.) P(S) = 0.6 P(S | A) = P(S | Pa) = (b) Are the events S = sale and Pa = passive approach independent? Explain. O Yes. The two events can occur together. O Yes. P(S) = P(S | Pa). O No. The two events cannot occur together. O No. P(S) # P(S | Pa). (c) Compute P(A and S) and P(Pa and S). (Enter your answers as fractions.) P(A and S) =[ P(Pa and S) = (d) Compute P(N) and P(N | A). (Enter your answers as fractions.) P(N) = P(N | A) =0 (e) Are the events / = no sale and A aggressive approach independent? Explain. O Yes. The two events can occur together. O No. P( N) # P(N | A). O Yes. P(N) = P(N | A). O No. The two events cannot occur together. (f) Compute P(A or S). (Enter your answer as a fraction.) P(A or S) = Need Help? Read It Watch It Viewing Saved Work Revert to Last Response