I need help with questions 3a and 3b

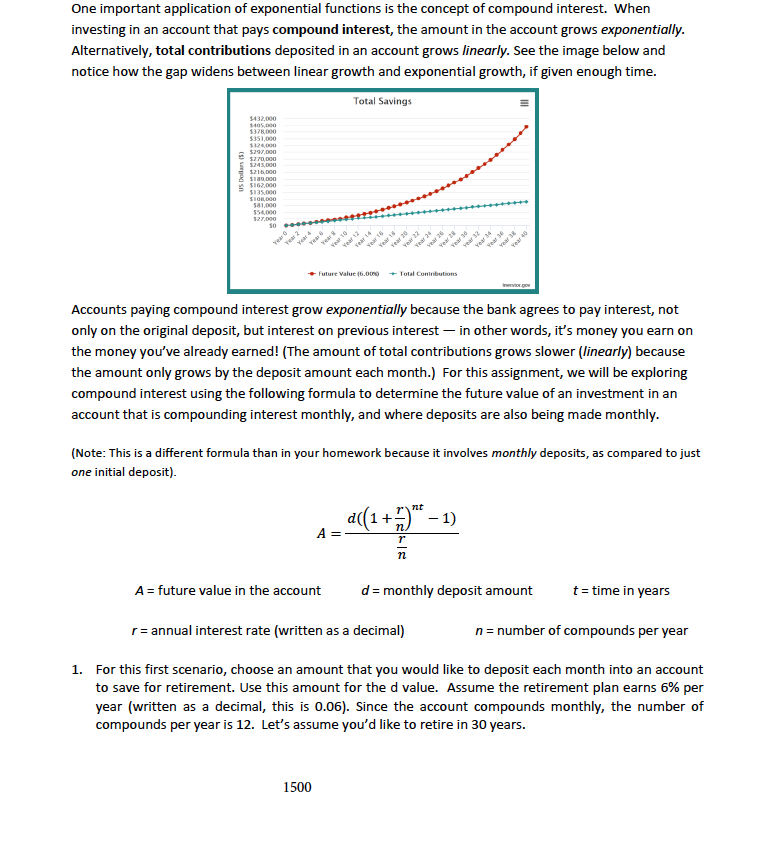
One important application of exponential functions is the concept of compound interest. When investing in an account that pays compound interest, the amount in the account grows exponentially. Alternatively, total contributions deposited in an account grows linearly. See the image below and notice how the gap widens between linear growth and exponential growth, if given enough time. Total Savings $351,000 $162.50 527.030 Year 35 Future Value (6.009) + Total Co Accounts paying compound interest grow exponentially because the bank agrees to pay interest, not only on the original deposit, but interest on previous interest - in other words, it's money you earn on the money you've already earned! (The amount of total contributions grows slower (linearly) because the amount only grows by the deposit amount each month.) For this assignment, we will be exploring compound interest using the following formula to determine the future value of an investment in an account that is compounding interest monthly, and where deposits are also being made monthly. (Note: This is a different formula than in your homework because it involves monthly deposits, as compared to just one initial deposit). d ( ( 1 + ) - 1) A = future value in the account d = monthly deposit amount t = time in years r = annual interest rate (written as a decimal) n = number of compounds per year 1. For this first scenario, choose an amount that you would like to deposit each month into an account to save for retirement. Use this amount for the d value. Assume the retirement plan earns 6% per year (written as a decimal, this is 0.06). Since the account compounds monthly, the number of compounds per year is 12. Let's assume you'd like to retire in 30 years. 1500a. Identify the values: d= 1500 r= 0.06 n= 12 t= 30 .005 (Enter this amount in the formula wherever you see an. b. Solve the given formula using the values identified above to find the total amount in your account after 30 years. You must show your work for credit. (Round the answer to the nearest dollar): A= 1500((1+ . 004 ) 13-30 (1+ DOG ) 30 =4.01267 1500( 4 02267 -1)=507257 1500 (5.07257 ) = 7633- 80281 7533. 86281 = 1504772.56 TA= 1504, 17'31 C. Reflect on your answer you got for part 1b. Does it look like a realistic and likely answer, or did you do something wrong in the previous steps? (Reflecting on your answer is an important part of doing real- world problems!) Yes it looks like a realistic number To check your answer, try going to the savings calculator at: https:/www.investor.gov/additional-resources/free-financial-planning-tools/compound-interest- calculator. Make sure that you set the inputs to the following: Initial investment: $0 (we do not have any money in the account when we begin saving) Monthly contributions: (your monthly deposit amount you chose) Length of time in years: (years until retirement) Estimated interest rate: (annual interest rate) Interest rate variance range: (For our problem, we will let this be 0) Compound Frequency: "monthly" "If you got a different answer than your answer in part (b) above, try to rework part (b) until they match. Did you use the correct order of operations?2. For this second scenario, let's assume you started saving 10 years earlier, giving your account more time to grow along the exponential curve. a) Assume all other variables remain the same as part la, but adjust your value for t to reflect 40 years until retirement instead of 30 years. How much money will be in the account in 40 years? (Remember, you must show your work for credit, but feel free to check your answer using the online calculator). *= 1500((1+ 00[) 12-40 - 1 ) 480 (1+ 004 ) = 10.9745 1500 (10.4740-1)= 945745 1500(495745 ) = 14936.18060 14934. 18050 = 7,987, 2360. 10 0.006 A= 2,987, 2310) b) How much extra money would you have in your retirement plan by saving for 40 years instead of 30 years? Show your work here: 2987 2136 1, 506, 773 1, 480 , 4 63 3. It's important to recognize that YOU only deposited a total of $(d x t x 12) into the account in each scenario. The rest of the money is the result of compound interest. a. How much interest was earned in each scenario? Show your work here:b. Reflect on the power of compounding interest using examples from this assignment to support your claims