I need help with some of the functions in the given code below. It is C++ and the instructions are all above the function

#ifndef LIST_H

#define LIST_H

#include

#include

// using namespace std;

template

class List

{

private:

// struct for singly-linked list nodes

struct Node

{

T data;

Node *next;

Node( const T & d = T{}, Node * n = nullptr)

: data{ d }, next{ n } { }

};

public:

// constructors

List( ) {

init( );

}

~List( ) {

clear( );

}

/**

* Disclaimer: C++ conventions tell us that we should have a couple

* of additional constructors here (a copy constructor, assignment operator

* etc.)

*

* However, to keep things simple for now we will ignore that convention

* (since the exposure to C++ is pretty variable it seems -- some students

* having taken 141 before last semester; some students coming from 107,

* etc.)

*/

/**

* function: clear

* desc: makes the calling list empty (but the list still

* exists).

*/

void clear(){

Node * p = front;

Node *pnext;

while(p != nullptr) {

pnext = p->next;

delete p;

p = pnext;

}

front = back = nullptr;

}

/**

* TODO

*

* function: length

* desc: returns the length of the calling list

*

* REQUIREMENTS: this is a working implementation, but

* it takes linear time.

*

* Your job (todo): make modifications so that this

* operation becomes constant time (O(1)).

*

* This task is different from most others in that most of

* the "real" work you do to make this work

* in O(1) time will be in _other_ functions which affect

* the length of lists.

*

* HINT: you are free to add data members to the List class...

* maybe for "bookkeeping"??

*/

int length( ) const {

Node *p = front;

int n=0;

while(p != nullptr) {

n++;

p = p->next;

}

return n;

}

public:

// Return true if the list is empty, false otherwise.

bool is_empty( ) const {

return front == nullptr;

}

void print() const {

Node *p = front;

std::cout

while(p != nullptr) {

std::cout data

p = p->next;

}

std::cout

}

void push_front(const T & data) {

front = new Node(data, front);

if(back == nullptr)

back = front;

}

bool pop_front(T &val) {

Node *tmp;

if(front==nullptr)

return false;

val = front->data;

tmp = front;

front = front->next;

delete tmp;

if(front==nullptr)

back = nullptr;

return true;

}

void push_back(const T & val) {

Node *tmp = new Node(val, nullptr);

if(front == nullptr) {

front = back = tmp;

}

else {

back->next = tmp;

back = tmp;

}

}

bool remove_first(const T &x) {

Node *p, *tmp;

T dummy;

if(front==nullptr) return false;

if(front->data == x) {

pop_front(dummy);

return true;

}

p = front;

while(p->next != nullptr) {

if(x == p->next->data) {

tmp = p->next;

p->next = tmp->next;

if(tmp == back)

back = p;

delete tmp;

return true;

}

p = p->next;

}

return false;

}

int slow_remove_all(const T &x) {

int n=0;

while(remove_first(x))

n++;

return n;

}

bool is_sorted() const {

Node *p = front;

while(p!=nullptr && p->next != nullptr) {

if(p->data > p->next->data)

return false;

p = p->next;

}

return true;

}

/** TODO

* function: count

* description: Counts number of occurrences

* of x in the list and returns that count.

*

* REQUIRMENT: Linear runtime (O(n) where n is the length

* of the list.)

*/

int count(const T &x) const {

return 0;

}

/* TODO

*

* function: pop_back

*

* if list is empty, we do nothing and return false

* otherwise, the last element in the list is removed, its

* value (data field) is assigned to the reference parameter

* data (so the removed element can be 'passed-back' to the

* caller) and true is returned.

*

* REQUIRMENT: Linear runtime (O(n) where n is the length

* of the list.)

*

*/

bool pop_back(T &data) {

return false;

}

/**

* TODO:

* function: equal_to

* description: returns true if calling List and parameter

* List other contain exactly the same sequence of values.

* Returns false otherwise.

*

* REQUIRMENT: Linear runtime (O(n) where n is MIN(len1,len2)

* and len1 and len2 are the respective lengths of the two lists.

**/

bool equal_to(const List &other) const {

return false; // placeholder

}

/**

* TODO: print in reverse order

*

* Try to do without looking at notes!

* Hints: recursive helper function

*

* REQUIRMENT: Linear runtime (O(n) where n is the length

* of the list.)

*/

void print_rev() const {

}

/* TODO

* For full credit, you cannot allocate any new memory!

*

* description: self-evident

*

* REQUIRMENT: Linear runtime (O(n) where n is the length

* of the list.)

*/

void reverse() {

}

/** TODO

* function: fast_remove_all

* description: same behavior/semantics as

* slow_remove_all. However, this function

* must guarantee linear time worst case

* runtime (hence, "fast").

*

* REQUIREMENT: linear worst-case runtime.

*

* Note: your solution may be either recursive or

* iteratieve.

**/

int fast_remove_all(const T &x) {

return 0;

}

/** TODO

* function: insert_sorted

*

* description: assumes given list is already in sorted order from

* smallest to largest and inserts x into the appropriate position

* retaining sorted-ness.

* Note 1: duplicates are allowed.

*

* Note 2: if given list not sorted, behavior is undefined/implementation

* dependent. We blame the caller.

* So... you don't need to check ahead of time if it is sorted.

*

*

* REQUIREMENTS:

*

* O(n) runtime

*/

void insert_sorted(const T &x) {

}

/** TODO

* function: merge_with

*

* description: assumes both list a and b are in

* sorted (non-descending) order and merges them

* into a single sorted list with the same

* elements.

*

* This single sorted list is stored in a while

* b becomes empty.

*

* if either of given lists are not sorted,

* we blame the caller and the behavior is

* implementation dependent -- i.e., don't worry

* about it!

*

* Condition in which both parameters are the same

* list (not merely "equal"), the function simply

* does nothing and returns. This can be tested

* with simple pointer comparison.

*

* Example:

*

* a: [2 3 4 9 10 30]

* b: [5 8 8 11 20 40]

*

* after call a.merge_with(b):

*

* a: [2 3 4 5 8 8 9 10 11 20 30 40]

* b: []

*

*

* REQUIREMENTS:

*

* Runtime Must be linear in the length of the

* resulting merged list (or using variables above,

* O(a.length()+b.length()).

*

* should not allocate ANY new list

* nodes -- it should just re-link existing

* nodes.

*/

void merge_with(List &other){

}

/**

* TODO

* function: clone

*

* description: makes a "deep copy" of the given list a

* and returns it (as a List pointer).

*

* NOTE: this functionality would normally be folded into

* a "copy constructor"

*

*/

List * clone() const {

return nullptr;

}

/**

* TODO

* function: prefix

*

* description: removes the first k elements from the

* calling list which are used to form a new list

* which is then returned.

*

* if n is the length of the given list, we have the

* following boundary conditions:

*

* if k==0:

* calling list unchanged and an empty list returned

* if k>=n:

* calling becomes empty and a list containing

* all elements previously in lst is returned.

*

* examples:

*

* EX1: lst: [2, 3, 9, 7, 8]

* k: 3

*

* call:

*

* List * pre = lst.prefix(3);

*

* after call:

* lst: [7, 8]

* returned list (prefix): [2, 3, 9]

*

* EX2 lst: [2, 3, 9, 7, 8]

* k: 0

*

* call:

*

* List * pre = lst.prefix(3);

*

* after call:

* lst: [2, 3, 9, 7, 8] (unchanged)

* returned list: []

*

* EX3 lst: [2, 3, 9, 7, 8]

* k: 5

*

* call:

*

* List * pre = lst.prefix(5);

*

* after call:

* lst: []

* returned list: [2, 3, 9, 7, 8]

*

* REQUIREMENTS:

*

* RUNTIME: THETA(n) worst case where n is the length of the given list

*

* ORDERING: the ordering of the returned prefix should be the same as

* in the given list

*

* MEMORY: for full credit, no new nodes should be

* allocated or deallocated; you should just

* "re-use" the existing nodes. HOWEVER, you will

* need to allocate a List object for the returned

* prefix (but, again, the underlying Nodes should be

* re-used from the calling list).

*/

List * prefix(unsigned int k) {

return nullptr;

}

/**

* TODO

* function: filter_leq

*

* description: removes all elements of the given list (lst) which

* are less than or equal to a given value (cutoff)

*

* A list containing the removed elements is returned.

*

* examples:

*

* EX1: lst: [4, 9, 2, 4, 8, 12, 7, 3]

* cutoff: 4

*

* after call:

* lst: [9, 8, 12, 7]

* returned list: [4, 2, 4, 3]

*

* -----------------------------------------

* EX2: lst: [6, 5, 2, 1]

* cutoff: 6

*

* after call:

* lst: []

* returned list: [6, 5, 2, 1]

*

* REQUIREMENTS:

*

* RUNTIME: THETA(n) where n is the length of the given list

*

* ORDERING: the ordering of the returned list should be the same as

* in the given list

*

* MEMORY: for full credit, no new nodes should be allocated or deallocated;

* you should just "re-use" the existing nodes. HOWEVER, you will

* need to allocate a LIST structure itself (i.e., for the returned

* list).

*

*/

List * filter_leq(const T & cutoff) {

return nullptr;

}

/**

* TODO

* function: concat

*

* description: concatenates the calling list with parameter list (other)

* The resulting concatenation is reflected the calling list; the

* parameter list (other) becomes empty.

*

* example:

*

* EX1: a: [2, 9, 1]

* b: [5, 1, 2]

*

* call:

* a.concat(b);

*

* after call:

*

* a: [2, 9, 1, 5, 1, 2]

* b: []

*

* REQUIREMENTS:

*

* runtime: O(1)

*

* sanity: this operation makes sense when a and b

* are distinct lists. For example, we don't

* want/allow the caller to do something like

* this:

*

* List *my_list = new List();;

*

* my_list->push_front(my_lst, 4);

* my_list->push_front(my_lst, 2);

*

* my_lst->concat(my_lst);

*

* your implementation must detect if it is being

* called this way. If so the function does nothing

* and (optionally) prints an error message to

* stderr.

*

*/

void concat(List &other) {

if(this == &other) {

std::cerr

std::cerr

return;

}

std::cout

}

/**

* TODO

*

* function: compare_with

* description: compares the calling list with parameter list (other)

* "LEXICALLY" (essentially a generalization of dictionary

* ordering).

*

* link: https://en.wikipedia.org/wiki/Lexicographical_order

*

* Return Value:

*

* o if the two lists are identical, 0 is returned.

* o if the calling list is lexically BEFORE the other list,

* -1 is returned

* o otherwise, the other list is lexically before the calling

* list and 1 (positive one) is returned.

*

* Properties and examples:

*

* The empty list is lexically before all non-empty lists

* (you can say it is "less than" all non-empty lists).

*

* Examples (using mathematical notation):

*

* [2 5 1]

*

* [4 1 3]

* "cartoon" in the dictionary).

*

* [4 5 6 1 2 3 9 9 9]

* ^ ^

* (they have a common prefix of length 4; but at

* the fifth position they differ and the left list

* is the winner (smaller) -- no need to look further)

*

*

* Templates?

*

* Since List is a template class, the elements of a particular

* list need not be integers. For example, we could have

* lists of strings.

*

* Good news: the exact same principle applies because

* strings can be compared just like integers can be compared!

*

* Great news: you don't need to think about this at all!

* The exact same code you would write if you assumed the element

* type is integer will work for other types like strings.

*

* Why? Because, for example, all of these operators:

*

* and >=

*

* all work on strings. They are not 'built-in' to C++, but

* the class string has "overloaded" these operators (they

* result in an appropriate function call).

*

* (In a subsequent exercise, we will do this kind of

* overloading ourselves!)

*

* Examples with lists of strings:

*

* ["egg", "goat"]

*

* ["zebra", "fun"]

*

* [Yes, the components of these lists are THEMSELVES compared

* lexically, but the string class is doing those comparisons)

*

*/

int compare_with(const List &other) const {

return 0;

}

/*

* TODO

*

* function: suffix_maxes

*

* desc: constructs a new list of the same length as the calling object

* with the value stored at position i of the new list is the MAXIMUM

* value in the suffix (or tail) of the calling list starting from

* position i.

*

* This new list is returned and the calling list is unchanged.

*

* Example:

*

* Given List: [6, -18, 12, 4, 1, 7, 2, 5 4]

* ^^^^^^^^^^^^^^^^

*

* New list: [12, 12, 12, 7, 7, 7, 5, 5, 4]

* ^

*

* (as a sub-example, the marked entry in the new list

* (marked with '^') is the max of the marked suffix in the

* given list (marked with a bunch of '^'s).

*

* REQUIREMENTS:

*

* Total Runtime: O(n)

* Calling list is unchanged.

*

*/

List * suffix_maxes() const{

return nullptr;

}

private:

Node *front;

Node *back;

void init( ) {

front = nullptr;

back = nullptr;

}

};

#endif

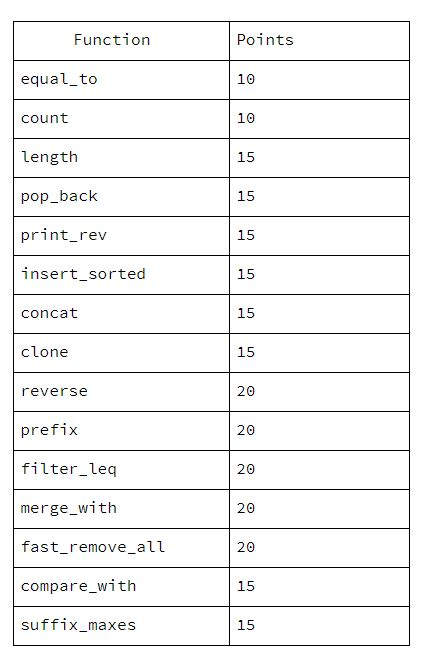
Function Points equal_to count 10 length pop_back print_rev insert_sorted concat 15 15 15 15 15 clone 15 reverse 20 prefiX filter_leq merge_with fast_remove_all compare with suffix_maxes 20 20 20 15 15