I need help with the following linear programming that neds to be solved using MATLAB. It's a short problem. The total number of lines shouldn't really be more than 10 lines. I can't post the .m files so I am posting the code for IpLV.m and Iphsolver under the question. Thanks!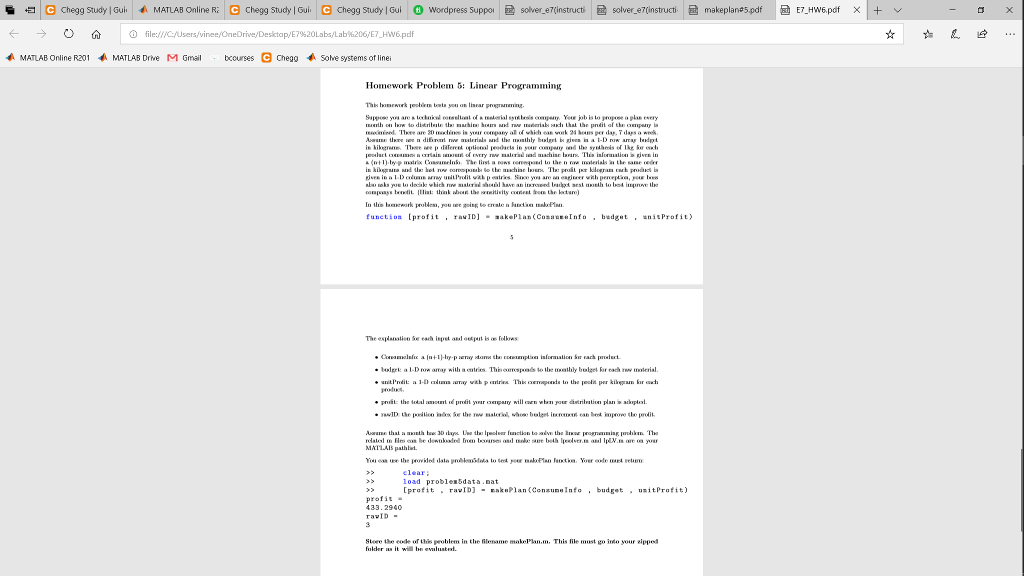

CODE FOR Ipsolver

function [optx,lambda,status,gamma] = lpsolver(c,A,b)

% Solves LP in standard form (see slidesotes)

% min c'*x, subject to Ax

% Makes direct call to lp236a.m from

% Returns optimal x (optx), dual variables (lambda), status (CHAR), and the

% optimal objective function (simply c'*optx). The

% dual variables are the derivative of the optimum value

%

[optx,~,lambda,~,status] = lpLV(c,A,b,[],[]);

if strcmp(status,'optimal')

gamma = c'*optx;

elseif strcmp(status,'primal infeasible')

status = 'infeasible';

gamma = inf;

elseif strcmp(status,'dual infeasible')

status = 'unbounded';

gamma = -inf;

else

status = 'unknown';

gamma = [];

end

CODE FOR IpLV solver

function [x,s,z,y,status] = lpLV(c,G,h,A,b,varargin)

% [x,s,z,y,status] = lpLV(c,G,h,A,b,x0,s0,y0,z0)

% Solves the primal-dual pair of LPs

% minimize c'*x maximize -h'*z - b'*y

% subject to G*x + s = h subject to G'*z + A'*y + c = 0

% A*x = b z >= 0.

% s >= 0

%

% Input arguments

% c n-vector

% G mxn-matrix with m >= 1; may be sparse or full

% A pxn-matrix with p >= 0; may be sparse or full

% h m-vector

% b p-vector

% x0, s0 (optional) primal starting point; must satisfy s0>0

% If x0=s0=[], x0=0, s0=1 is used.

% y0, z0 (optional) dual starting point; must satisfy z0>0

% If y0=z0=[], y0=0, z0=1 is used.

%

% Output arguments

% x,s,y,z: the primal and dual optimal solutions, or certificates of

% primal/dual infeasibility.

% status: string with possible values 'optimal', 'primal infeasible',

% 'dual infeasible', 'unknown'.

%

% We require Rank(A) = p and Rank([G;A]) = n. In other words,

% the matrix [0, A; A', G'*G] must be nonsingular.

%

% The following calling sequences are also valid:

% [x,s,z,y,status] = lp236a(c,G,h,A,b) means the same as

% [x,s,z,y,status] = lp236a(c,G,h,A,b,[],[],[],[]);

%

% [x,s,z,y,status] = lp236a(c,G,h,A,b,x0,s0) means the same as

% [x,s,z,y,status] = lp236a(c,G,h,A,b,x0,s0,[],[]);

%

% If status is `optimal':

% s>=0, z>=0

% and ||G*x+s-h||/max{1,||h||}

% and ||A*x-b||/max{1,||b||}

% and ||G'*z+A'*y+c||/max{1,||c||}

% and ( c'*x+h'*y+b'*z

% or (h'*z+b'*z

% or (c'*x

%

% If status is `primal infeasible', x=s=[] and y,z are a proof of primal

% infeasibility:

% z>=0 and ||G'*z + A'*y||

%

% If status is `dual infeasible': y=z=[] and x,s is a proof of dual

% infeasibility:

% s>=0 and ||G*x + s||

%

% If status is `unknown', the algorithm was unable to classify the

% LP, or the maximum number of iterations was exceeded, and

% x=s=y=z=[].

%

%

% (Lieven Vandenberghe, September 2005)

% SELF-DUAL EMBEDDING

%

% The primal and dual LPs are embedded in a self-dual LP with two

% additional variables tau, theta, and one extra slack variable lambda:

%

% minimize rc*theta

% subject to [ 0 h' b' c' ro ][ tau ] [lambda] [ 0 ]

% [-h 0 0 G ri ][ z ] [ s ] [ 0 ]

% [-b 0 0 A re ][ y ] + [ 0 ] = [ 0 ]

% [-c -G' -A' 0 rd ][ x ] [ 0 ] [ 0 ]

% [-ro -ri' -re' -rd' 0 ][theta] [ 0 ] [ rc]

% tau >= 0, z >= 0, lambda >= 0, s >= 0

%

% with

% rc = 1 + z0'*s0

% ri = h - G*x0 - s0

% re = b - A*x0

% rd = c + G'*z0 + A'*y0

% ro = -(c'*x0 + h'*z0 + b'*y0 + 1)

%

% Properties:

%

% 1. If s0 > 0, z0 > 0, then tau = theta = lambda = 1, z = z0, y = y0,

% x = x0, s = s0 are strictly feasible.

%

% 2. The optimal value is zero. The optimal solutions satisfy

% the complementarity conditions tau*lambda = 0, z'*s = 0.

%

% 3. If tau > 0 at the optimum, then lambda = 0, and

% x/tau, s/tau, z/tau, y/tau are primal and dual optimal

% for the original pair of LPs.

%

% 4. If tau = 0 and lambda > 0 at the optimum, and c'*x

% then the problem is dual infeasible and x is a certificate.

%

% 5. If tau = 0 and lambda > 0 at the optimum, and h'*z + b'*y

% then the problem is primal infeasible and y,z are a certificate.

%

% 6. The central path, defined as the set of feasible solutions

% that satisfy tau*lambda = mu, z.*s = mu, converges to a strictly

% complementary solution (in particular, one with tau+lambda > 0).

% ALGORITHM

%

% The self-dual problem is an LCP

%

% C*u + D*v + w = f

% -D'*u + E*v = g

% u'*w = 0

% u >= 0, v >= 0

%

% with

% u = [tau; z], v = [y; x; theta], w = [lambda; s]

% f = [0; 0], g = [0; 0; rc]

% C = [0, h'; -h, 0]

% D = [b', c', ro; 0, G, ri]

% E = [0, A, re; -A', 0, rd; -re', -rd', 0]

%

% We solve the LCP using a predictor-corrector method to follow

% the central path, which is defined by

%

% C*u + D*v + w = f

% -D'*u + E*v = g

% u.*w = mu

% u > 0, w > 0

%

% 1. Start at strictly feasible points

%

% 2. Compute affine scaling directions

%

% C*dua + D*dva + dwa = 0

% -D'*dua + E*dva = 0

% u.*dwa + w.*dua = -u.*w

%

% 3. Determine suitable mu

%

% 4. Compute centering-corrector directions

%

% C*duc + D*dvc + dw = 0

% -D'*duc + E*dvc = 0

% u.*dwc + w.*duc = mu - dua.*dwc

%

% 5. Update u,v,w

SHOWPROGRESS = 0;

MAXITERS = 100;

ABSTOL = 1e-8;

RELTOL = 1e-8;

FEASTOL = 1e-8;

MINSLACK = 1e-8;

STEP = 0.99;

EXPON = 3;

if size(c,2) ~= 1, c=c'; end;

n = size(c,1);

if size(G,2) ~= n | (~isempty(A) & size(A,2) ~= n)

error('Dimensions of c, A, G do not match.');

end;

if size(h,2) ~= 1, h=h'; end;

m = size(h,1);

if size(G,1) ~= m

error('Dimensions of G and h do not match.');

end;

if size(b,2) ~= 1, b=b'; end;

p = size(b,1);

if ~isempty(A)

if size(A,1) ~= p,

error('Dimensions of A and b do not match.');

end;

else

A = zeros(0,n);

b = zeros(0,1);

end;

sparselp = issparse(A) & issparse(G);

if nargin == 5

x = zeros(n,1);

s = ones(m,1);

z = ones(m,1);

y = zeros(p,1);

end;

if nargin == 6

error('Give x0 and s0 to specify primal starting point.');

end;

if nargin >= 7

x = varargin{1};

s = varargin{2};

z = ones(m,1);

y = zeros(p,1);

if xor(isempty(x), isempty(s))

error('Give x0 and s0 to specify primal starting point.');

end;

if isempty(x)

x = zeros(n,1);

s = ones(m,1);

end;

if min(s)

error('s0 must be positive.');

end;

end;

if nargin == 8

error('Give y0 and z0 to specify dual starting point.');

end;

if nargin == 9

y = varargin{3};

z = varargin{4};

if p>0

if xor(isempty(y), isempty(z))

error('Give y0 and z0 to specify dual starting point.');

end;

end;

if isempty(y)

y = zeros(p,1);

z = ones(m,1);

end;

if min(z)

error('z0 must be positive.');

end;

end

if (nargin > 9)

error('Too many input arguments.');

end;

rc = 1+z'*s;

ri = h-G*x-s;

re = b-A*x;

rd = c+G'*z+A'*y;

ro = -(c'*x+h'*z+b'*y+1);

nrmh = max([1,norm(h)]);

nrmb = max([1,norm(b)]);

nrmc = max([1,norm(c)]);

tau = 1;

lambda = 1;

theta = 1;

u = [tau; z]; dimu = m+1;

v = [y; x; theta]; dimv = p+n+1;

w = [lambda; s]; dimw = m+1;

if p == 0 & issparse(G)

perm = symmmd(G'*G);

else

perm = [];

end;

if SHOWPROGRESS

disp(sprintf(' %16s%14s', 'duality gap', 'residuals'));

disp(sprintf('%9s%8s%10s%6s', 'abs.', 'rel.', 'primal', 'dual'));

end

for iters = 1:MAXITERS

tau = u(1); z = u(1+[1:m]);

y = v(1:p); x = v(p+[1:n]); theta = v(p+n+1);

lambda = w(1); s = w(1+[1:m]);

% STOPPING CRITERION

pcost = c'*x/tau;

dcost = -(h'*z + b'*y)/tau;

absgap = u'*w/(tau*tau);

if dcost > 0

relgap = absgap/dcost;

elseif pcost

relgap = absgap/(-pcost);

else

relgap = Inf;

end;

hresi = G*x+s; resi = h - hresi/tau;

hrese = A*x; rese = b-hrese/tau;

hresd = G'*z + A'*y; resd = c+hresd/tau;

pres = max([norm(resi)rmh, norm(rese)rmb]);

dres = norm(resd)rmc;

hpres = max([norm(hresi), norm(hrese)]);

hdres = norm(hresd);

if SHOWPROGRESS

disp(sprintf('%2d:% 7.0e% 8.0e% 8.0e% 8.0e ', ...

iters-1, absgap, relgap, pres, dres));

end;

if pres

relgap

status='optimal';

x = x/tau; s = s/tau;

z = z/tau; y = y/tau;

return;

elseif h'*z+b'*y

status = 'primal infeasible';

x = []; s = [];

t = abs(h'*z+b'*y);

z = z/t; y = y/t;

return;

elseif c'*x

status = 'dual infeasible';

t = abs(c'*x);

x = x/t; s = s/t;

z = []; y = [];

return;

end;

% FACTORIZATION

%

% We will need to solve two sets of equations

%

% S*dz + Z*ds = r1

% lambda*dtau + tau*dlambda= r2

% h'*dz + b'*dy + c'*dx + ro*dtheta + dlambda = r3

% -h*dtau + G*dx + ri*dtheta + ds = r4

% -b*dtau + A*dx + re*dtheta = r5

% -c*dtau - G'*dz - A'*dy + rd*dtheta = r6

% -ro*dtau - ri'*dz - re'*dy - rd'*dx = r7

%

% with different righthand sides.

%

% We will do this by solving

%

% [-Z\S 0 G] [dz] [-h ri] [dtau ] [r4-Z 1]

% [ 0 0 A]*[dy] + [-b re]*[ ] = [ r5 ]

% [ G' A' 0] [dx] [ c -rd] [dtheta] [ -r6 ]

%

% [-h' -b' -c'] [dz] [-lambda/tau ro] [dtau ] [r3-r2/tau]

% -[ ]*[dy] + [ ]* [ ] = [ ]

% [ri' re' rd'] [dx] [ -ro 0 ] [dtheta] [ r7 ]

%

% and taking ds = Z\(r1-S*dz), dlambda = (r2-lambda*dtau)/tau

%

% Write the 2x2 block system as

%

% H11*dX1 + H12*dX2 = G1

% H21*dX1 + H22*dX2 = G2.

%

% We solve this by elimination: first solve

%

% (H22 - H21*(H11\H12)) * dX2 = G2 - H21*(H11\G1)

%

% and take dX1 = H11\G1 - (H11\H12)*dX2

%

% To prepare for all of this, we factor the matrix

%

% [-S/Z 0 G]

% H11 = [ 0 0 A]

% [ G' A' 0]

%

% then solve for H11\H12, and compute H22 - H21*(H11\H12).

% factor H11 = [-S/Z, 0, G; 0, 0, A; G',A', 0]

fac = kkt_fac(s./z,G,A,perm);

if isempty(fac)

if iters == 1

error('Rank(A)

else

error('KKT matrix is singular.');

end;

end

% compute [Gz; Gy; Gx] = H11 \ H12

[solx1,soly1,solz1] = kkt_sol(s./z,G,A,fac,c,-b,-h,perm);

[solx2,soly2,solz2] = kkt_sol(s./z,G,A,fac,-rd,re,ri,perm);

Gx = [solx1 solx2];

Gy = [soly1 soly2];

Gz = [solz1 solz2];

% compute T = H22 - H21*(H11\H12)

T = [-lambda/tau, ro; -ro, 0] + ...

[-h', -b', -c'; ri', re', rd'] * [Gz;Gy;Gx];

% COMPUTE AFFINE SCALING STEP

%

% [-Z\S 0 G] [dz] [-h ri] [dtau ] [r4-Z 1]

% [ 0 0 A]*[dy] + [-b re]*[ ] = [ r5 ]

% [ G' A' 0] [dx] [ c -rd] [dtheta] [ -r6 ]

%

% [-h' -b' -c'] [dz] [-lambda/tau ro] [dtau ] [r3-r2/tau]

% -[ ]*[dy] + [ ]* [ ] = [ ]

% [ri' re' rd'] [dx] [ -ro 0 ] [dtheta] [ r7 ]

%

% ds = (r1-s.*dz)./z;

% dlambda = (r2-lambda*dtau)/tau;

%

% with

%

% r1 = -s.*z

% r2 = -tau*lambda

% r3 = -(h'*z + b'*y + c'*x + ro*theta + lambda)

% r4 = -(-h*tau + G*x + ri*theta + s)

% r5 = -(-b*tau + A*x + re*theta)

% r6 = -(-c*tau - G'*z - A'*y + rd*theta)

% r7 = rc - (-ro*tau - ri'*z - re'*y - rd'*x)

r1 = -s.*z;

r2 = -tau*lambda;

r3 = -(h'*z + b'*y + c'*x + ro*theta + lambda);

r4 = -(-h*tau + G*x + ri*theta + s);

r5 = -(-b*tau + A*x + re*theta);

r6 = -(-c*tau - G'*z - A'*y + rd*theta);

r7 = rc - (-ro*tau - ri'*z - re'*y - rd'*x);

[dx1,dy1,dz1] = kkt_sol(s./z,G,A,fac,-r6,r5,r4-r1./z,perm);

sol = T \ ([r3-r2/tau;r7] + ...

[-h' -b' -c'; ri' re' rd'] * [dz1;dy1;dx1]);

dz = dz1 - Gz*sol;

dy = dy1 - Gy*sol;

dx = dx1 - Gx*sol;

dtau = sol(1);

dtheta = sol(2);

ds = (r1-s.*dz)./z;

dlambda = (r2-lambda*dtau)/tau;

du = [dtau; dz];

dv = [dy; dx; dtheta];

dw = [dlambda; ds];

% COMPUTE STEP TO BOUNDARY

step = 1/max([-du./u; -dw./w]);

mu = (u'*w)/(m+1);

muaff = (u + step*du)'*(w + step*dw)/(m+1);

sigma = (muaff/mu)^EXPON;

% COMPUTE CENTERING-CORRECTOR STEP

%

% [-Z\S 0 G] [dz] [-h ri] [dtau ] [r4-Z 1]

% [ 0 0 A]*[dy] + [-b re]*[ ] = [ r5 ]

% [ G' A' 0] [dx] [ c -rd] [dtheta] [ -r6 ]

%

% [-h' -b' -c'] [dz] [-lambda/tau ro] [dtau ] [r3-r2/tau]

% -[ ]*[dy] + [ ]* [ ] = [ ]

% [ri' re' rd'] [dx] [ -ro 0 ] [dtheta] [ r7 ]

%

% ds = (r1-s.*dz)./z;

% dlambda = (r2-lambda*dtau)/tau;

%

% with

%

% r1 = sigma*mu - dsa.*dza

% r2 = sigma*mu - dtaua*dlambdaa

% r3 = 0

% r4 = 0

% r5 = 0

% r6 = 0

% r7 = 0

r1 = sigma*mu - ds.*dz;

r2 = sigma*mu - dtau*dlambda;

r3 = zeros(size(r3));

r4 = zeros(size(r4));

r5 = zeros(size(r5));

r6 = zeros(size(r6));

r7 = zeros(size(r7));

[dx1,dy1,dz1] = kkt_sol(s./z,G,A,fac,-r6,r5,r4-r1./z,perm);

sol = T \ ([r3-r2/tau;r7] + ...

[-h' -b' -c'; ri' re' rd'] * [dz1;dy1;dx1]);

dzc = dz1 - Gz*sol;

dyc = dy1 - Gy*sol;

dxc = dx1 - Gx*sol;

dtauc = sol(1);

dthetac = sol(2);

dsc = (r1-s.*dzc)./z;

dlambdac = (r2-lambda*dtauc)/tau;

duc = [dtauc; dzc];

dvc = [dyc; dxc; dthetac];

dwc = [dlambdac; dsc];

% COMPUTE STEPS, STEP LENGTHS AND UPDATE

du = du+duc; dv = dv+dvc; dw = dw+dwc;

step = min(STEP/max([-du./u; -dw./w]), 1.0);

u = u + step*du; v = v + step*dv; w = w + step*dw;

end;

disp(['Maximum number of iterations exceeded.']);

status = 'unknown';

x=[]; s=[]; y=[]; z=[];

function fac = kkt_fac(d,G,A,varargin)

% fac = kkt_fac(d,G,A,[]);

% fac = kkt_fac(d,G,A);

%

% [-diag(d) 0 G ]

% Factors K = [ 0 0 A ]

% [ G' A' 0 ]

%

%

% fac = kkt_fac(d,G,A,perm);

%

% [ -diag(d) 0 G(:,perm) ]

% factors [ 0 0 A(:,perm) ]

% [ G(:,perm)' A(:,perm)' 0 ]

%

%

% Input arguments:

% - d: m-vector, with m>=1. Must have positive elements.

% - G: mxn, with m>=1 and n >= 1.

% - A: pxn, with p>=1, or an empty matrix

% - perm: (optional) permutation vector of length n.

%

%

%

% Output argument is a structure fac.

%

% - If K is singular, fac = [].

%

% - If p=0 and K is nonsingular, then fac.F is the cholesky factor R

% in G'*diag(1./d)*G = R'*R.

% L is sparse if G and A are sparse, and full otherwise.

%

% - If p>0, K is nonsingular, and A or G are full, then fac.L, fac.U,

% fac.P are the LU factors of the matrix

% [ 0, A; A', G'*diag(1./d)*G ] = P'*L*U

% P is a permutation matrix, stored as a sparse matrix,

% L and U are full.

%

% - If p>0, K is nonsingular, and A and G are sparse, then

% fac.L, fac.U, fac.P, fac.Q are the LU factors of the matrix

% [ 0, A; A', G'*diag(1./d)*G ] = P'*L*U*Q'

% P and Q are permutation matrices. P, Q, L and U are sparse.

RANKTOL = 1e-10; % triangular U is singular if min(|U(i,i)|)

MINSLACK = 0.0; % d(i) must be greater than MINSLACK

if size(d,2) ~= 1

d=d';

end;

m = size(d,1);

if min(d)

error('Elements of d must be positive.');

end;

if size(G,1) ~= m

error('Dimensions of G and d do not match.');

end;

if m

error('G must have at least one row.');

end;

n = size(G,2);

if ~isempty(A) & (size(A,2) ~= n)

error('Dimensions of A and G do not match.');

end;

p = size(A,1);

if nargin

perm = [];

else

perm = varargin{1};

end;

if ~isempty(perm)

G = G(:,perm);

if p > 0,

A = A(:,perm);

end;

end;

if nargin > 4

error('Too many input arguments.');

end;

e = 1./d;

if p == 0

if issparse(G)

[fac.R,flag] = chol(G'*spdiags(e,0,m,m)*G);

else

[fac.R,flag] = chol(G'*(G .* e(:,ones(1,n))));

end;

if flag,

fac = [];

end;

else

if issparse(G) & issparse(A)

[fac.L, fac.U, fac.P, fac.Q] = lu(...

[ sparse(p,p), A; A', G'*spdiags(e,0,m,m)*G ]);

else

[fac.L, fac.U, fac.P] = lu(...

[ zeros(p,p), full(A);

full(A)', G'*(G .* e(:,ones(1,n))) ] );

fac.P = sparse(fac.P);

end;

if min(abs(diag(fac.U)))

fac = [];

end;

end;

function [x,y,z] = kkt_sol(d,G,A,fac,rx,ry,rz,varargin)

% [x,y,z] = kkt_sol(d,G,A,fac,rx,ry,rz,perm);

% [x,y,z] = kkt_sol(d,G,A,fac,rx,ry,rz,[]);

% [x,y,z] = kkt_sol(d,G,A,fac,rx,ry,rz)

%

% [-diag(d) 0 G ] [z] [rz]

% solves KKT system [ 0 0 A ] [y] = [ry]

% [ G' A' 0 ] [x] [rx]

%

% with KKT matrix previously factored by kkt_fac

%

% Input arguments:

% - d: m-vector, with m>=1. Must have positive elements.

% - G: mxn, with m>=1 and n >= 1.

% - A: pxn, with p>=1, or an empty matrix

% - fac: output of fac = kkt_fac(d,G,A,perm) or fac = kkt_fac(d,G,A)

% - perm: (optional) permutation vector of length n.

% If perm is specified, fac contains a factorization of

%

% [ -diag(d) 0 G(:,perm) ]

% [ 0 0 A(:,perm) ]

% [ G(:,perm)' A(:,perm)' 0 ]

%

%

% Output argument: solution, or x=y=z=[] if KKT matrix is singular.

if size(d,2) ~= 1

d=d';

end;

m = size(d,1);

if size(G,1) ~= m

error('Dimensions of G and d do not match.');

end;

if m

error('G must have at least one row.');

end;

n = size(G,2);

if ~isempty(A) & (size(A,2) ~= n)

error('Dimensions of A and G do not match.');

end;

p = size(A,1);

if size(rx,2) ~= 1

rx = rx';

end;

if size(rx,1) ~= n

error('Length of rx does not match A, G, d.');

end;

if isempty(ry),

ry = zeros(0,1);

end;

if size(ry,2) ~= 1

ry = ry';

end;

if size(ry,1) ~= p

error('Length of ry does not match A, G, d.');

end;

if size(rz,2) ~= 1

rz = rz';

end;

if size(rz,1) ~= m

error('Length of rz does not match A, G, d.');

end;

if nargin

perm = [];

else

perm = varargin{1};

end;

if ~isempty(perm)

G = G(:,perm);

if p > 0

A = A(:,perm);

end;

rx = rx(perm);

end;

if nargin > 8

error('Too many input arguments.');

end;

if isempty(fac)

error('Matrix is singular.');

end;

if p == 0

x = fac.R \ ( fac.R' \ ( rx + G'*(rz./d) ));

y = zeros(0,1);

else

if issparse(G) & issparse(A)

sol = fac.Q * (fac.U \ (fac.L \ (fac.P * [ry; rx+G'*(rz./d)])));

else

sol = fac.U \ (fac.L \ (fac.P * [ry; rx+G'*(rz./d)]));

end;

y = sol(1:p);

x = sol(p+[1:n]);

end;

z = (G*x-rz)./d;

if ~isempty(perm)

x(perm) = x;

end