I need help with this question:
- In computer science, we often struggle to find efficient algorithms for problems, so we conjecture that they are hard. As we saw with graph isomorphisms, assuming this allows us to get zero-knowledge schemes. Let's use another common conjecture to form another zero-knowledge proof scheme. For the purposes of this section, p is a very large prime number.
- Definition 4.1. An integer g (mod p) is called a generator if every number in {1, 2, . . . , p − 1} can be written as g^a (mod p) for some a.
- Here, in the modular arithmetic setting, we charge costs a little differently: adding or multiplying two numbers mod p costs $1. Making random numbers still costs the same. An algorithm is efficient in modular arithmetic if it's a polynomial in log2 p, the number of binary digits in p.
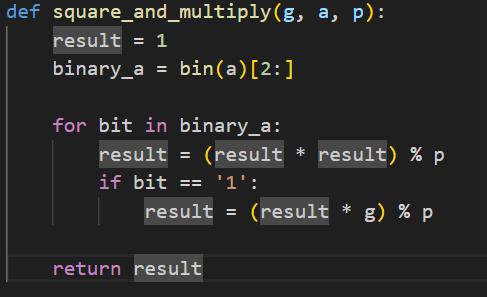
- Question  (Already been answered)- Devise an efficient algorithm for computing g^a (mod p).

          - Answer - 

 

- It turns out that undoing the operation is much more difficult.
 

 

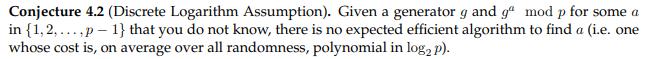
Before we can harness this, we should see why modular arithmetic plays nicely with randomness

 - Question 2: Show that given a fixed number N, then if we randomly pick R in {0, 1, . . . , p− 1}, then N + R mod p is equal in distribution to R.
- Question 3: Show that given a fixed number N not equivalent to 0 (mod p), if we randomly pick R in {1, 2, . . . , p − 1}, then NR mod p is equal in distribution to R.

def square_and_multiply(g, a, p): result = 1 binary_a = bin(a) [2:] for bit in binary_a: result = (result * result) % p if bit == '1': result = (result g) % p return result