I need the answer for question 3. Ive attached the whole assignment in pictures. But only need help for question 3. I am copy pasting my bisection algorithm and improved euler algorithm . Bisection :

function [r, resarray] = bisect(f,a,b,tol,maxiter)

%f = @(x) x^3-3; %a = -2; %b = 4; %tol = 10^-6; %maxiter=100;

if sign(f(a)) == sign(f(b)) disp('error message') r= [] ; resarray= []; return end

for iter = 1:maxiter r = (a+b)/2; resarray(iter) = abs(f(r));

if abs(f(r))

end if sign(f(r)) == sign(f(a)) a=r; else b=r; end end

Improved Euler:

function y = ieuler(func,y0,t0,tf,Nt) % f = function f % t0 and tf are startng and ending times respectively % initital condition vector, y0 % number of timesteps Nt

%func = @(t,x) 2*(x^3) + 7*x; %feed in these on command window %t0=0; %tf=10; %y0=0; %Nt=200;

h=(tf-t0)/Nt; %time interval y=zeros(1,Nt+1); %preallocate y t=t0:h:tf; %array of timesteps y(:,1)=y0; %column vector, set intial condition

for k=1:Nt s1=func(t(k),y(:,k)); s2=func(t(k+1),y(:,k+1)); y(:,k+1) = y(:,k)+(s1+s2)*(h/2); %improved end y=[t' y']; end

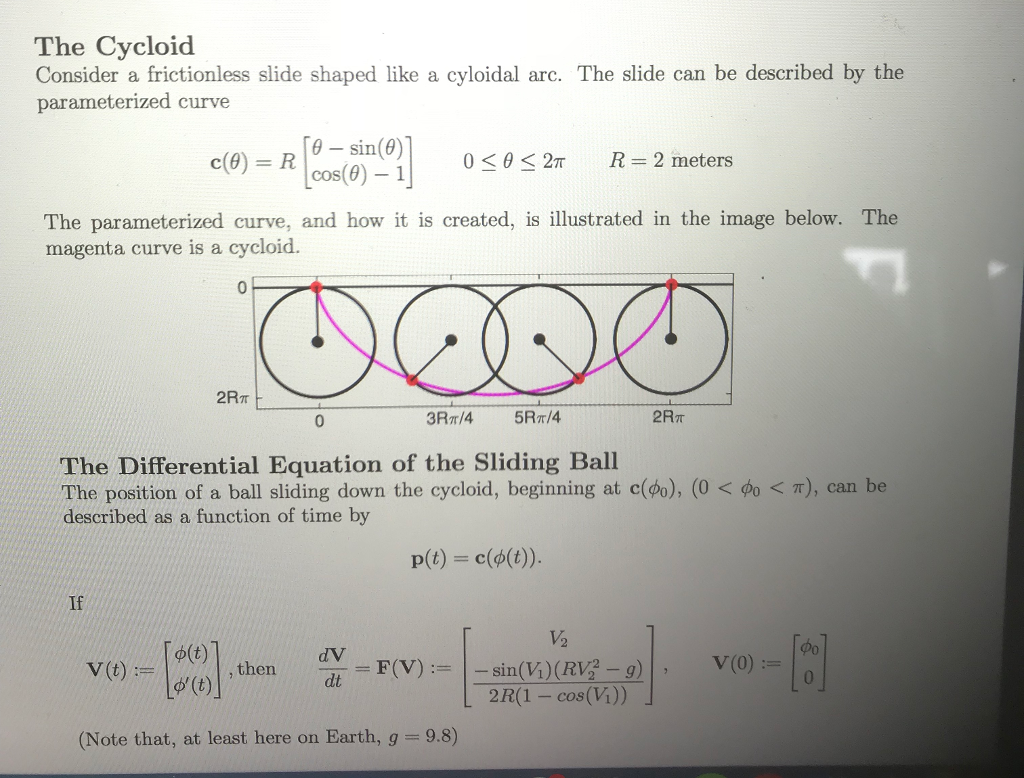
2. (10 points) Before completing the next task, describe how you think the initial position of the ball on the cycloid halfpipe will affect the time it takes to reach the bottom. Will a ball beginning closer to the bottom or closer to the top reach the bottom first? Explain why you think so. 3. Write a script titled HW7.m that carries out the following tasks (20 points) Apply your bisection algorithm to the objective function described above to compute the time it takes a ball to reach the bottom of the cycloidal halfpipe for the following values of o: 20 20 20' 20 Illustrate your findings in a plot (oo vs. ts). Set the y-limits of your plot to be [0, 3]. Use an initial bisection interval of [1, 2], a tolerance of 10-10, and mar of 40 bisection iterations. Set the Improved Euler timesteps per second to, Ntps 100. (20 points) Use your Irnproved Euler code to approximate ?(t) for the nineteen starting positions above over the interval [0, 4tb) using M 100(4tb)1 timesteps. Plot each t vs. ?(t) on the same plot. 4. (10 points) What does tautochrone mean and how is that reflected in your findings? Explain how the intersections of the curves in your second plot correspond to the results of your first plot. Bonus (10 points) Create a matlab script that animates 5 balls (each a different color) falling down a cycloid slide at the same time, with each ball starting at the values 6 6' 6' 66 2. (10 points) Before completing the next task, describe how you think the initial position of the ball on the cycloid halfpipe will affect the time it takes to reach the bottom. Will a ball beginning closer to the bottom or closer to the top reach the bottom first? Explain why you think so. 3. Write a script titled HW7.m that carries out the following tasks (20 points) Apply your bisection algorithm to the objective function described above to compute the time it takes a ball to reach the bottom of the cycloidal halfpipe for the following values of o: 20 20 20' 20 Illustrate your findings in a plot (oo vs. ts). Set the y-limits of your plot to be [0, 3]. Use an initial bisection interval of [1, 2], a tolerance of 10-10, and mar of 40 bisection iterations. Set the Improved Euler timesteps per second to, Ntps 100. (20 points) Use your Irnproved Euler code to approximate ?(t) for the nineteen starting positions above over the interval [0, 4tb) using M 100(4tb)1 timesteps. Plot each t vs. ?(t) on the same plot. 4. (10 points) What does tautochrone mean and how is that reflected in your findings? Explain how the intersections of the curves in your second plot correspond to the results of your first plot. Bonus (10 points) Create a matlab script that animates 5 balls (each a different color) falling down a cycloid slide at the same time, with each ball starting at the values 6 6' 6' 66