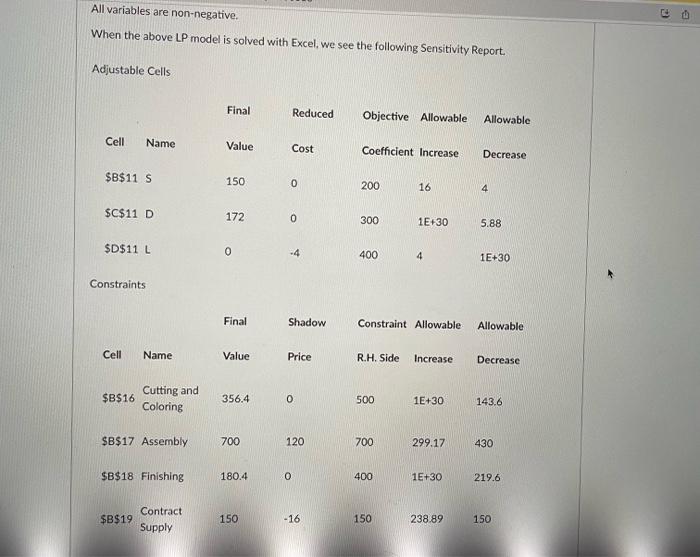
I need the final answer only please. Thank you.

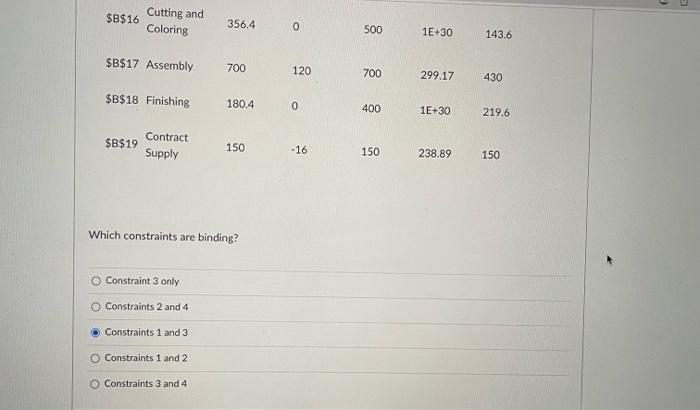
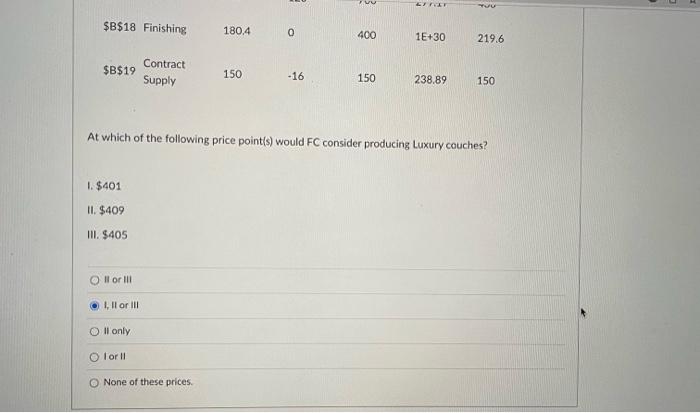
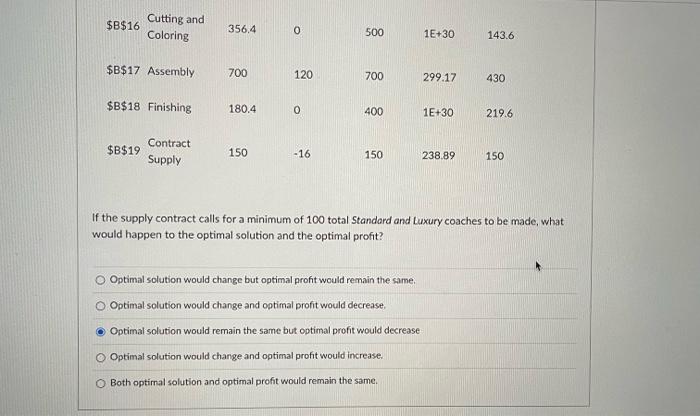
The Furniture City (FC) company makes 3 kinds of couches: (1) Standard, (2) Deluxe, and (3) Luxury styles. Each couch goes through 3 production departments: (1) Cutting and Coloring. (2) Assembly, and (3) Finishing. The total number of hours available each month in each of the above departments is 500 . 700 and 400 , respectively. The time (in hours) required by 3 departments for making each couch and the profit per couch are listed below. The company has a contract of supplying at least a total of 150 Standard and Luxury couches per month. The company would like to make a production plan to maximize its total profit. Define S, D, L as the variables for the numbers of Standard, Deluxe and Luxury couches produced by the company. Then the corresponding LP model is built as follows: Max200S+300D+400L All variables are non-negative. All variables are non-negative. When the above LP model is solved with Excel, we see the following Sensitivitu Ranart Which constraints are binding? Constraint 3 only Constraints 2 and 4 Constraints 1 and 3 Constraints 1 and 2 Constraints 3 and 4 If the available finishing hours are cut down by 250 , what would happen to the optimal solution and the optimal profit? Optimal solution would remain the same but optimal profit would decrease. Both optimal solution and optimal profit would remain the same. Optimal solution would change and optimal profit would decrease. Optimal salution would change but optimal profit would remain the same. Optimal solution would change and optimal profit would increase, At which of the following price point(s) would FC consider producing Luxury couches? 1. $401 II. $409 III. $405 II or III 1. II or III II only Ior 11 None of these prices. If the supply contract calls for a minimum of 100 total Standard and Luxury coaches to be made, what would happen to the optimal solution and the optimal profit? Optimal solution would change but optimal profit would remain the same. Optimal solution would change and optimal profit would decrease. Optimal solution would remain the same but optimal profit would decrease Optimal solution would change and optimal profit would increase. Both optirnal solution and optimal profit would remain the same