I need to return a Dictionary, with the keys as the node, and weight as the value

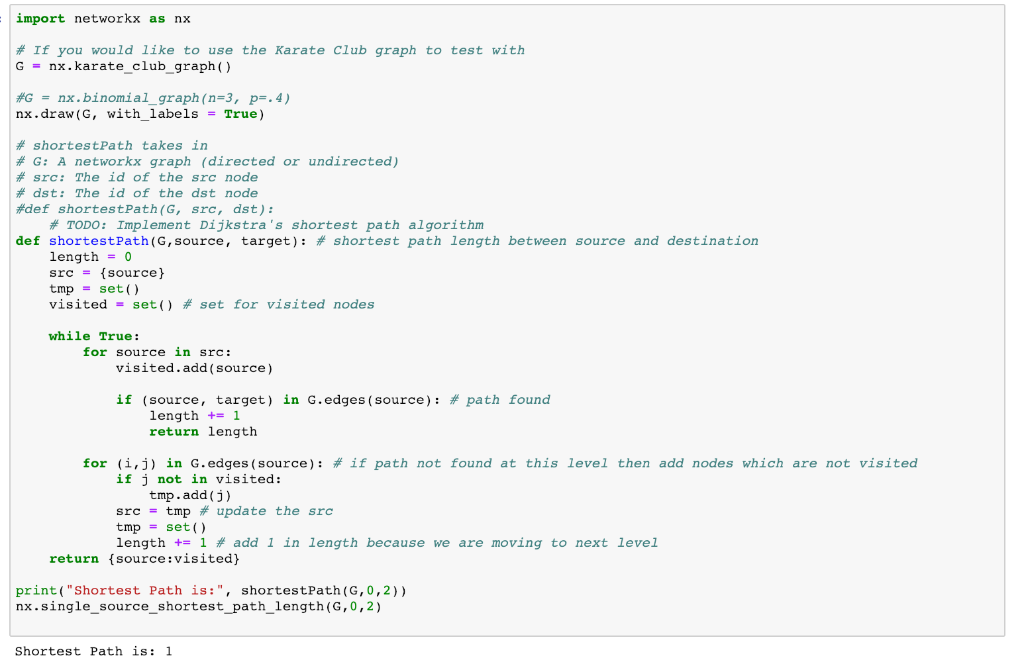
Part 1: Calculating the Shortest Path Use Dijkstra's shortest path algorithm to calculate the shortest path between any two nodes in a graph. The function signature (function name and parameters) are provided. You can use the Karate Club graph as the graph input. You may only use the NetworkX nodes) and edges0 functions. import networkx as nx # If you would like to use the Karate Club graph to test with G-nx.karate_club_graph # shortestPath takes in # G: A networkx graph (directed or undirected) # src : The id of the src node # dst: The id of the dst node def shortestPath (G, src, dst): import networkx as nx # If you would like to use the Karate Club graph to test with G nx.karate club graph () G- nx . binomial-graph ( n-3, p-.4) nx.draw(G, with-labels = True) # shortestPath takes in # G: A networkx graph (directed or undirected) # src : The id of the src node dst: The id of the dst node #def shortestPath (G, src, dst): # TODO : Implement Dijkstra's shortest path algorithm def shortestPath (G, source , target): # shortest path length between source and destination length 0 src = {source} tmpset() visited- set() # set for visited nodes while True: for source in src: visited.add (source) if (source , target) length + 1 in G.edges ( source): #path found return length for (1.3) in G.edges (source): # if path not found at this level then add nodes which are not visited if j not in visited: tmp.add(j) src -tmp # update the src tmpset() length += 1 # add 1 in length because we are moving to next level return source:visited) print( "Shortest Path is:", shortestPath (G,0,2)) nx.single_sourceshortest_path length (G,0,2) Shortest Path is: 1 Part 1: Calculating the Shortest Path Use Dijkstra's shortest path algorithm to calculate the shortest path between any two nodes in a graph. The function signature (function name and parameters) are provided. You can use the Karate Club graph as the graph input. You may only use the NetworkX nodes) and edges0 functions. import networkx as nx # If you would like to use the Karate Club graph to test with G-nx.karate_club_graph # shortestPath takes in # G: A networkx graph (directed or undirected) # src : The id of the src node # dst: The id of the dst node def shortestPath (G, src, dst): import networkx as nx # If you would like to use the Karate Club graph to test with G nx.karate club graph () G- nx . binomial-graph ( n-3, p-.4) nx.draw(G, with-labels = True) # shortestPath takes in # G: A networkx graph (directed or undirected) # src : The id of the src node dst: The id of the dst node #def shortestPath (G, src, dst): # TODO : Implement Dijkstra's shortest path algorithm def shortestPath (G, source , target): # shortest path length between source and destination length 0 src = {source} tmpset() visited- set() # set for visited nodes while True: for source in src: visited.add (source) if (source , target) length + 1 in G.edges ( source): #path found return length for (1.3) in G.edges (source): # if path not found at this level then add nodes which are not visited if j not in visited: tmp.add(j) src -tmp # update the src tmpset() length += 1 # add 1 in length because we are moving to next level return source:visited) print( "Shortest Path is:", shortestPath (G,0,2)) nx.single_sourceshortest_path length (G,0,2) Shortest Path is: 1