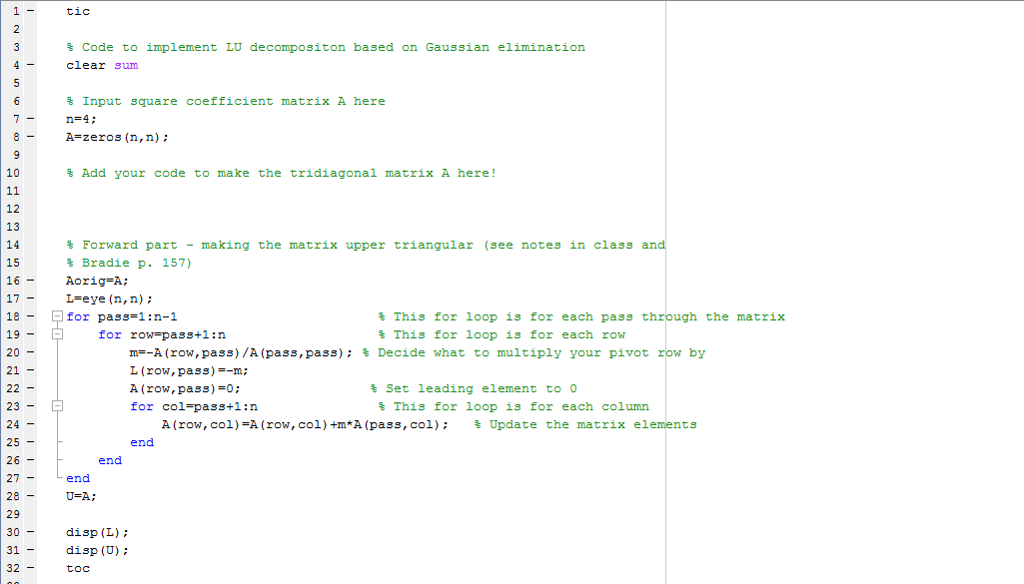
I tried using the code but i don't get it.

1. Write a MATLAB script to create an n x n tridiagonal matrix (where n is a variable you specify at the beginning of your script) with entries of -2 along the main diagonal and entries of 1 along the diagonals just below and just above the main diagonal, i.e. 2 1 (1) 2. Next, write your own script to implement these formulas to find the LU decomposition for a tridiagonal matrix A. Check your script by finding the LU decomposition of the matrix you made in #1 with n 4. You should have 1 3/2 (2) 1 -4/3 5/4 3. Now add two lines to your code for finding an LU decomposition for a tridiagonal matrix. In line 1, write 'tic'. On the last line of your MATLAB script, write toc When you run the script now, MATLAB should print to the command window an approximate amount of time elapsed while running the commands between 'tic' and 'toc' Use your code to find the LU decomposition for this tridiagonal matrix for n 10, 100, 500, 1000 Write down the approximate amount of time elapsed for each run. (You do not need to write down the LU decompositions or even print them to the screen!) 4. Next, we will repeat #3 using the LU decomposition script (based on Gaussian elimination without pivoting) that you downloaded last week. I have re-posted the script with lines commented out that we will not need, and have added 'tic' and 'toc' to the beginning and end of the script. Download this script and copy and paste your code that produces the tridiagonal matrix A. Now find the LU decomposition for this tridiagonal matrix using this Gaussian-elimination- based method for n 10, 100,500, 1000. Write down the approximate amount of time elapsed for each run. You do not need to write down the LU decompositions or even print them to the screen!) 5. Recall that Gaussian elimination takes O(n3) operations; i.e., if n is large, when you double n, you can expect the method to take roughly 8 times as long. Compare the time it took MATLAB in #4 for n 500 and n 1000 and check whether these times are approximately consistent with this expected increase in elapsed time