i want solution by java

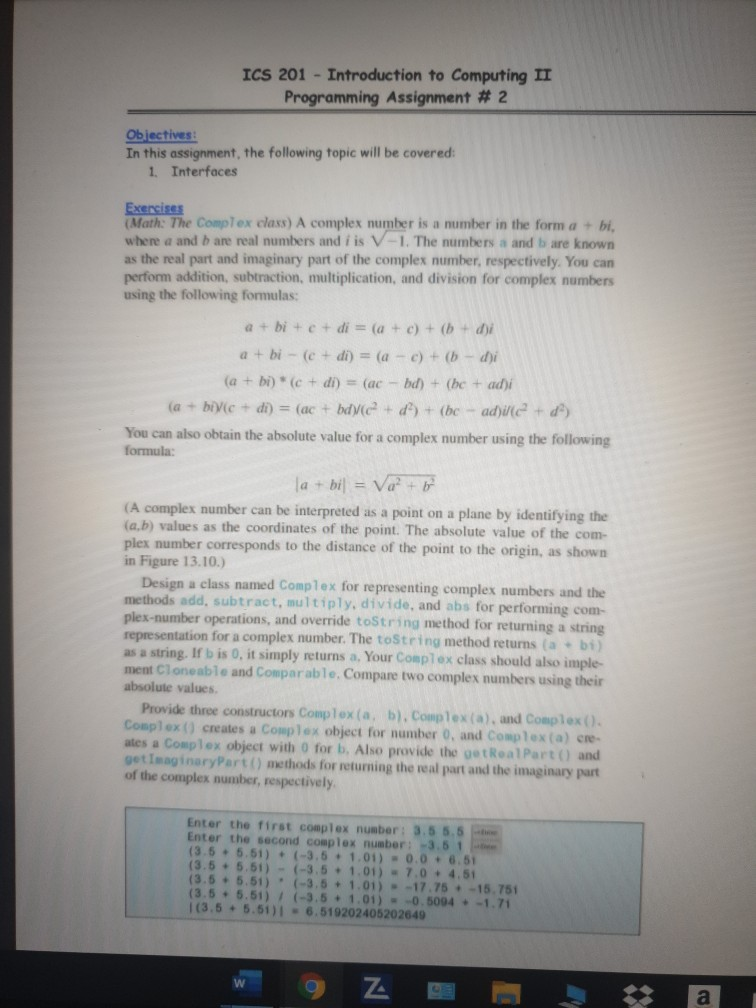
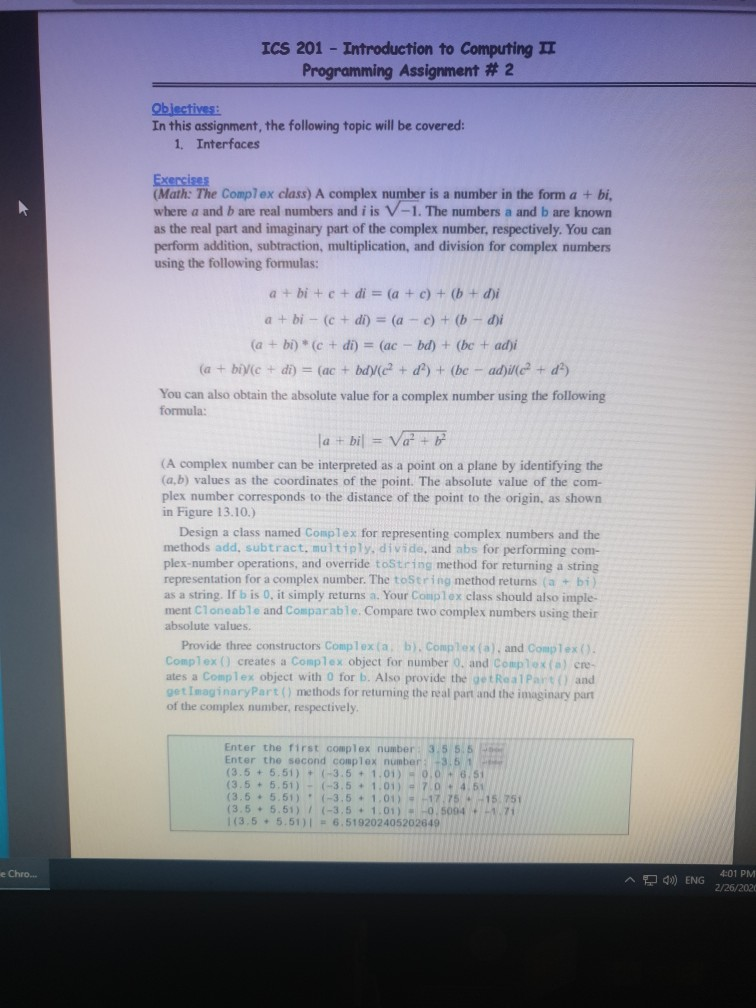
ICS 201 - Introduction to Computing IT Programming Assignment # 2 Objectives: In this assignment, the following topic will be covered: 1. Interfaces Exercises (Math: The Complex class) A complex number is a number in the form a + bi. where a and b are real numbers and iis V-1. The numbers a and b are known as the real part and imaginary part of the complex number, respectively. You can perform addition, subtraction, multiplication, and division for complex numbers using the following formulas: a + bi + c + di = (a + c) + (b + d)i a + bi - (c + di) = (a - c) + (b - di (a + bi) * (c + di) = (ac - bd) + (bc + adji (a + b)(c + di) = (ac + bd (e? + d) + (be - adi/c? + da You can also obtain the absolute value for a complex number using the following formula: la + bil = Vo? + b (A complex number can be interpreted as a point on a plane by identifying the (a,b) values as the coordinates of the point. The absolute value of the com- plex number corresponds to the distance of the point to the origin, as shown in Figure 13.10.) Design a class named Complex for representing complex numbers and the methods add, subtract, multiply, divide, and abs for performing com- plex-number operations, and override tostring method for returning a string representation for a complex number. The toString method returns (a + bi as a string. If bis 0, it simply returns a. Your Complex class should also imple ment Cloneable and comparable. Compare two complex numbers using their absolute values. Provide three constructors Complex ( a b). Complex (a). and Complex (). Complex () creates a complex object for number 0. and Complex (a) cre- ates a Complex object with O for b. Also provide the getReal Part) and getImaginary Part() methods for returning the real part and the imaginary part of the complex number, respectively. Enter the first complex number 3.5 5.5 Enter the second complex number-3.61 (3.5 + 5.51) + (-3.5 + 1.01) - 0. 0 6 .51 (3.5 -5.51) - (-3.5 - 1.01) 7.0 - 4.51 (3.5 -5.51) (-3.5 - 1.01) = -17.75 15.751 (3.5 +5.51) (-3.5 + 1.01) -0.5004 -1.71 1(3.5 - 5.51) = 6.519202405202649 e Chro... 4:01 PM 00) ENG 2/26/2020 ICS 201 - Introduction to Computing II Programming Assignment # 2 Objectives: In this assignment, the following topic will be covered: 1. Interfaces Exercises (Math: The Complex class) A complex number is a number in the form a + bi, where a and are real numbers and iis V-1. The numbers and bare known as the real part and imaginary part of the complex number, respectively. You can perform addition, subtraction, multiplication, and division for complex numbers using the following formulas: a + bi + e + di = (a + c) + ( + di a + bi - (c + di) = (a - c) + (1 - di (a + b)(c + di) = (ac - bd) + (be + adi (a + bivic + di) = (ac + bd)/(c + d) + (be - ad)ile + d) You can also obtain the absolute value for a complex number using the following formula: la+bil = Va+ b (A complex number can be interpreted as a point on a plane by identifying the (a,b) values as the coordinates of the point. The absolute value of the com- plex number corresponds to the distance of the point to the origin, as shown in Figure 13.10.) Design a class named Complex for representing complex numbers and the methods add, subtract, multiply, divide, and abs for performing com- plex-number operations, and override toString method for returning a string representation for a complex number. The toString method returns (a + b) as a string. If bis 0, it simply returns a, Your Complex class should also imple ment Cloneable and comparable. Compare two complex numbers using their absolute values Provide three constructors Complex (a, b). Complex (a), and Complex(). Complex () creates a Complex object for number 0, and complexa) ere ates a Complex object with o for b. Also provide the getRealPart() and getimaginaryPart() methods for returning the real part and the imaginary purt of the complex number, respectively Enter the first complex number: 3.5 5.5 Enter the second complex number: -3.51 (3.6. 5.51) - (-3.6 - 1.01) - 0.0 - 6.51 (3.5 . 5.51) - (-3.5 - 1.01) - 7.0. 4.51 (3.5 . 5.51) (-3.5 - 1.01) --17.75 .-15.751 (3. 5 5 .51) (-3.5 1.01) 0.5094 -1.71 (3.5 . 5.51) - 6.519202405202649 9 Z. 9