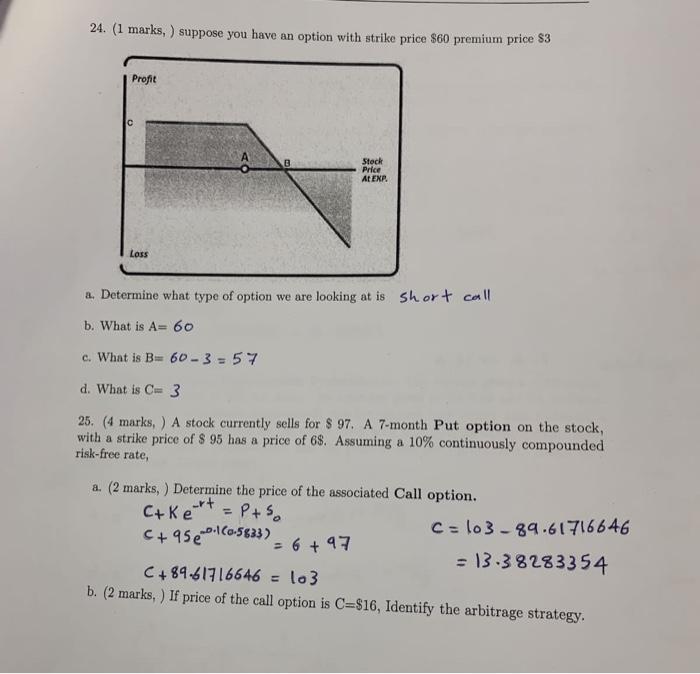
i want the correct answers for this

mathematic go up by % 18 or fall by 19 %. if the one-perlod risk free rate is 2%. (4 marks, ) Suppose a stocks is currently trading for 64, and in one period will either a. (3 marks, ) what is the price of a European put option that expire in one period and has an exercise price of 628 by using the replicating portfolio model? b. 1 marks, ) Are there an arbitrage opportunities, If price of the put option is P = $4.31 K kos 4= Vo-vd Su-sd o.1o.16 75.52-51.84 429054 V. 62.75.52 25.52 13 TO 64 51.84 10.16 B = Ve - S.A [+r 10.16 - 51.846.424.54) -31-76682 1 + 0.02 V62-51.84 64+ (64x 13.75.32 64-C54x19)5154 Vco) 5.4+B 264(-0.424.54)+31.76682 = 4.307364 4.31= 4.3 arbitrage. 27. (3 marks, ) Using Risk-Neutral Probabilities. The current price a continuous- dividend paying stock is 978 per share. Its volatility given to be 0.19 and its dividend yield is 0.04 The continuous compounded, risk-free interest rate equals 0.02 Consider a 0.345 958-strike European put option on the above stock with nine months to expiration using a three-period forward binomial tree, find the price of this put option. (Not: round each answer to 4 digit decimal place) 3 n=3, T = 2 / 4 ha Sund uz ger-sontorn Sun eco.or-0.0474 +0.1957 saldu dzer-s)-osa Le 0.02 -0.044 -0.196 sddd 1 P' I te su lte 1917 24. (1 marks, ) suppose you have an option with strike price 860 premium price $3 Profit C B Stock Price ATENP Loss a. Determine what type of option we are looking at is short call b. What is A= 60 c. What is B. 60 - 3 = 57 d. What is C 3 25. (4 marks, ) A stock currently sells for $ 97. A 7-month Put option on the stock, with a strike price of $ 95 has a price of 68. Assuming a 10% continuously compounded risk-free rate, Ca Kert C+95 +1(0-5823) a. (2 marks, ) Determine the price of the associated Call option. = Pts. C = 103-89.61716646 = 6 + 97 = 13.38283354 C+84.61716646 = 103 b. (2 marks, ) If price of the call option is C=$16, Identify the arbitrage strategy. -55 365 2 28. (3 marks, ) Consider a European call option with the following data: the company does not pay dividends. The standard deviation(volatility) is 0.84 per year. The risk-free rate is 0.8. stock has a current price of 888 Using the Black-Scholes formula, what is the price for 68 days European call option on with a strike price of 48S? (Not: round each answer to 4 digit decimal place) die In C5/PVCK) + In [88/43.02096 0.84 V68 pvC1+0.8) 385 OVT 2 0.84 168 di: 1.9738 +0. 0.18128 365 = 2.155-8 da = di-off = 2.155.8 0.84/08 C = $xAcc) - PVCK) ( d ) -88C9852 ) -43.2096 ( 9647.25) - 45 1942.0436 29. (3 marks, ) A nine-month American put option on a non-dividend-paying stock has a strike price of $49. The stock price is $50, the risk-free rate is 5% per annum, and the volatility is 30% per annum. Using a three-step binomial tree we calculate the option price Hint: p = 0.5043 a. Determine if it would be optimal to exercise early or not. b. What the price of the option at time- = 0.89627 PVCK): 0.84627048) = 43.02096 1.79251 365 Bolded values are a result of exercise Growth factor per step, a- 1.0125 Probability of up move, pl 0.5043 Up step size, u 1.1618 Down step size, d-0.8607 78.41561 67.49294 8.09171 58.09171 1.429187 50 4.289225 50 2.91968 43.0854 7.306214 43.0854 5.964601 37.04091 11.050 31188141 17.11859 Node Time: 0.0000 0.2500 0.5000 0.7500 mathematic go up by % 18 or fall by 19 %. if the one-perlod risk free rate is 2%. (4 marks, ) Suppose a stocks is currently trading for 64, and in one period will either a. (3 marks, ) what is the price of a European put option that expire in one period and has an exercise price of 628 by using the replicating portfolio model? b. 1 marks, ) Are there an arbitrage opportunities, If price of the put option is P = $4.31 K kos 4= Vo-vd Su-sd o.1o.16 75.52-51.84 429054 V. 62.75.52 25.52 13 TO 64 51.84 10.16 B = Ve - S.A [+r 10.16 - 51.846.424.54) -31-76682 1 + 0.02 V62-51.84 64+ (64x 13.75.32 64-C54x19)5154 Vco) 5.4+B 264(-0.424.54)+31.76682 = 4.307364 4.31= 4.3 arbitrage. 27. (3 marks, ) Using Risk-Neutral Probabilities. The current price a continuous- dividend paying stock is 978 per share. Its volatility given to be 0.19 and its dividend yield is 0.04 The continuous compounded, risk-free interest rate equals 0.02 Consider a 0.345 958-strike European put option on the above stock with nine months to expiration using a three-period forward binomial tree, find the price of this put option. (Not: round each answer to 4 digit decimal place) 3 n=3, T = 2 / 4 ha Sund uz ger-sontorn Sun eco.or-0.0474 +0.1957 saldu dzer-s)-osa Le 0.02 -0.044 -0.196 sddd 1 P' I te su lte 1917 24. (1 marks, ) suppose you have an option with strike price 860 premium price $3 Profit C B Stock Price ATENP Loss a. Determine what type of option we are looking at is short call b. What is A= 60 c. What is B. 60 - 3 = 57 d. What is C 3 25. (4 marks, ) A stock currently sells for $ 97. A 7-month Put option on the stock, with a strike price of $ 95 has a price of 68. Assuming a 10% continuously compounded risk-free rate, Ca Kert C+95 +1(0-5823) a. (2 marks, ) Determine the price of the associated Call option. = Pts. C = 103-89.61716646 = 6 + 97 = 13.38283354 C+84.61716646 = 103 b. (2 marks, ) If price of the call option is C=$16, Identify the arbitrage strategy. -55 365 2 28. (3 marks, ) Consider a European call option with the following data: the company does not pay dividends. The standard deviation(volatility) is 0.84 per year. The risk-free rate is 0.8. stock has a current price of 888 Using the Black-Scholes formula, what is the price for 68 days European call option on with a strike price of 48S? (Not: round each answer to 4 digit decimal place) die In C5/PVCK) + In [88/43.02096 0.84 V68 pvC1+0.8) 385 OVT 2 0.84 168 di: 1.9738 +0. 0.18128 365 = 2.155-8 da = di-off = 2.155.8 0.84/08 C = $xAcc) - PVCK) ( d ) -88C9852 ) -43.2096 ( 9647.25) - 45 1942.0436 29. (3 marks, ) A nine-month American put option on a non-dividend-paying stock has a strike price of $49. The stock price is $50, the risk-free rate is 5% per annum, and the volatility is 30% per annum. Using a three-step binomial tree we calculate the option price Hint: p = 0.5043 a. Determine if it would be optimal to exercise early or not. b. What the price of the option at time- = 0.89627 PVCK): 0.84627048) = 43.02096 1.79251 365 Bolded values are a result of exercise Growth factor per step, a- 1.0125 Probability of up move, pl 0.5043 Up step size, u 1.1618 Down step size, d-0.8607 78.41561 67.49294 8.09171 58.09171 1.429187 50 4.289225 50 2.91968 43.0854 7.306214 43.0854 5.964601 37.04091 11.050 31188141 17.11859 Node Time: 0.0000 0.2500 0.5000 0.7500