

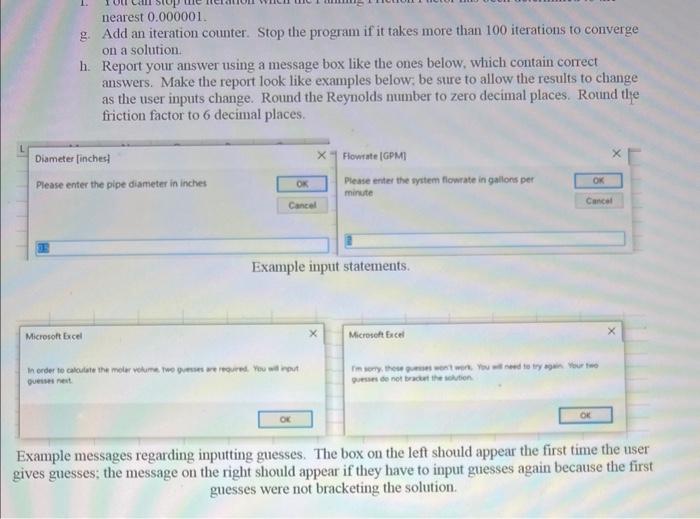
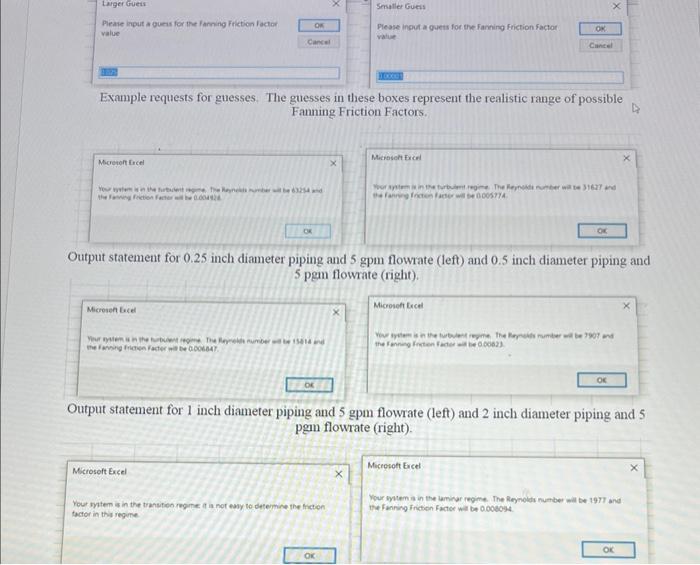
I want to create an intetactive app wich will help engineers deteraine the Fanning Friction Factor for water systems at rocm temperahure in smooth pipes. The app will nun on smart watches. so 1 'ma a lithe worried about the computing power requised by the app, so we will use different tectaniques under different conditions To determine the friction fictor, we will use the vou Kanman equation. waich unfortunately, is implicit. and thus we will need to use iteration schemes to find the solution to the equation. The von Karmage equation is given by: f/212.5ln[Re8f]+1.75 Where: f= Fanning Friction Factor [dimensionless] Re = Reynolds Number Specific tostructions a. Use input boxes to ask the use for impottant parameters for the system. Make then look like the exaumles given below. a. Pipe dianeter in inches b. Systeu flowrate in gallons per minute b. Calculase the Reynolds number. Use the following paraueters for rocen tempentare wate: a. Density =62.4bm/A3 b. Viscosity =1cP c. If the systenu will be in the laminar regiave (Re-2100), calculate the Fanning Friction Factor and report it to the user. Make the report look like examples below: be sure to allow the revalts to change as the user inpets change. End the progan atter the report. Round the Reynolds nuaber to zero decimal places. Roind the fiction factor to 6decinal places. d. If the system will be in the transition regine (2100 Re 4000), report that to the user. Make the report look like exauples below; be sure to allow the results to change as the user ingats chamge End the proaram after the report. Round the Reyuolds mumber to zero decimal places e. If the system will be in the tarbulent regine, you will iterme a wolution to the von Karman equation a. I have this theoty that the iteration will go best if you alienate techniques. So, on the first iteration loop. I want you to use the bisectiou method to determine the next guess. On the secoud iteration loop. I want you to use the Secant method to detemine the next guess. On the third iteration loop, I want you to nse the Newton method to deteruine the next guess. Then, repeat this pattem, as mauy times as necessary. iteration loop, I want you to use the bisection method to determine the next guess. On the second iteration loop. I want you to use the Secant method to determine the next guess. On the third iteration loop. I want you to use the Newton method to determine the next guess. Then, repeat this pattem, as many times as necessary. b. Ask the user to supply to starting guesses. Since we are going to be using the bisection method, you need to verify that these two starting guesses bracket the solution. Make the user prompts look like the ones below. Do not let them proceed in the program without entering valid guesses. Be sure that you give them the example message if you have to ask them for guesses again. c. The Bisection Method can be executed as normal d. The Secant Method can be executed as normal with one change. You will keep the new guess. You will also keep one of the two guesses from the previous iteration loop. Keep the one that keeps the solution bracketed. e. You can use the Newton Method using both of the guesses. This will allow you to calculate TWO potential new guesses. You will keep only one of them. i. We want to keep the 'better' of the two guesses. 1. It seems odd to judge guesses, but we can. Since the correct solution would cause our function to become zero, the best of the two new guesses would be the one which has a function evaluation closest to zero (either positive or negative). ii. You will keep one of the two guesses from the previous iteration loop. Keep the one that keeps the solution bracketed. f. You can stop the iteration when the Fanning Friction Factor has been determined to the nearest 0.000001 . g. Add an iteration counter. Stop the program if it takes more than 100 iterations to converge on a solution. h. Report your answer using a message box like the ones below, which contain correct answers. Make the report look like examples below: be sure to allow the results to change as the user inputs change. Round the Reynolds number to zero decimal places. Round the friction factor to 6 decimal places. Example input statements. Example messages regarding inputting guesses. The box on the left should appear the first time the user gives guesses; the message on the right should appear if they have to input guesses again because the first guesses were not bracketing the solution. Example requests for guesses. The guesses in these boxes represent the realistic range of possible Fanning Friction Factors. Output statement for 0.25 inch diameter piping and 5gpm flowrate (left) and 0.5 inch diameter piping and 5 pgen flowrate (right). Output statement for 1 inch diameter piping and 5 gpm flowrate (left) and 2 inch diameter piping and 5 pgin flowrate (right). tactor in this regite Output statement for 4 inch diameter piping and 5 gpm flowrate (left) and 8 inch diameter piping and 5 gpm flowrate (right)











