I was able to figure out how to do part A but I am struggling with how to do B,C, and D. Any guidance would be great. Thank you
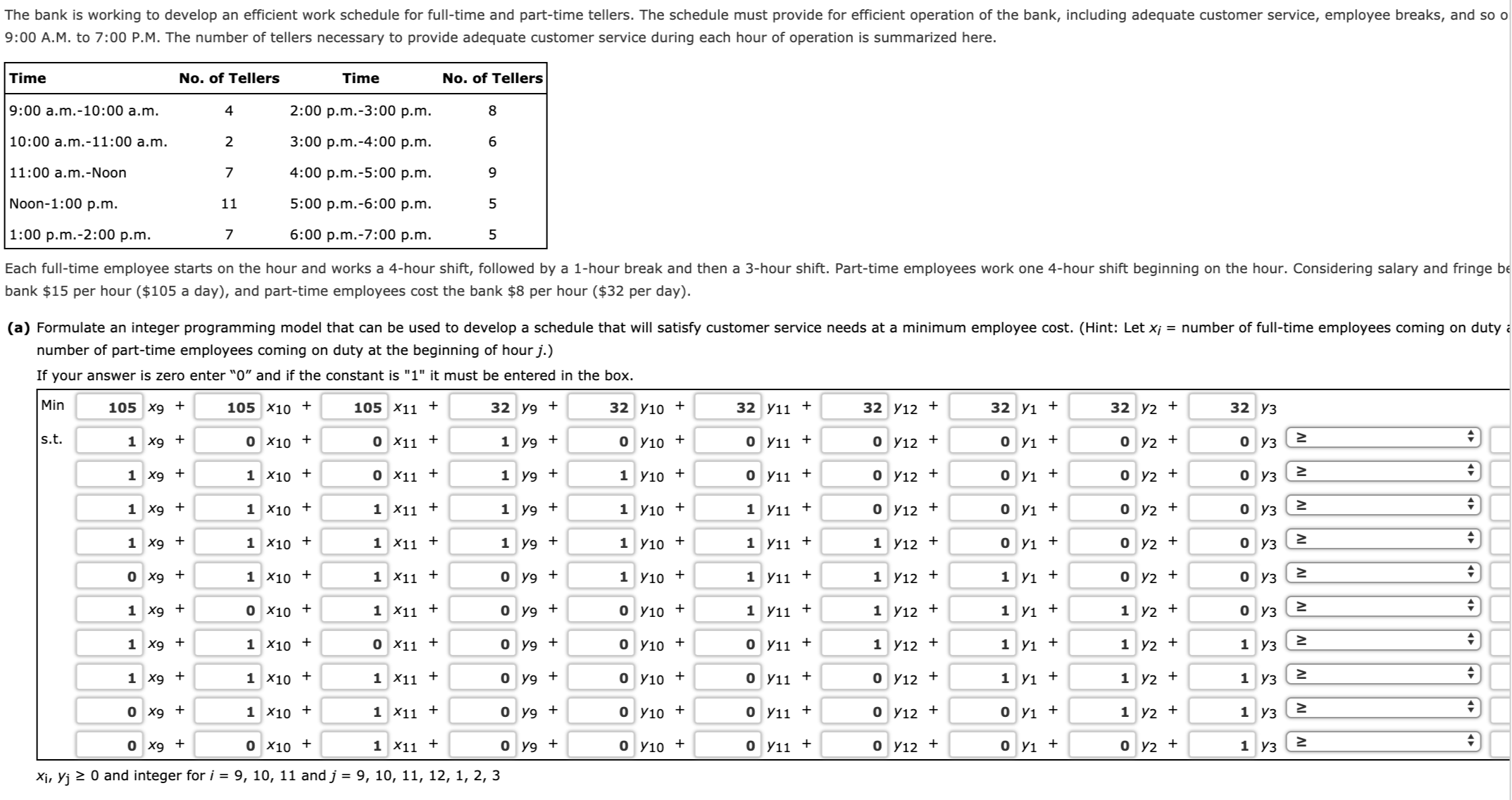
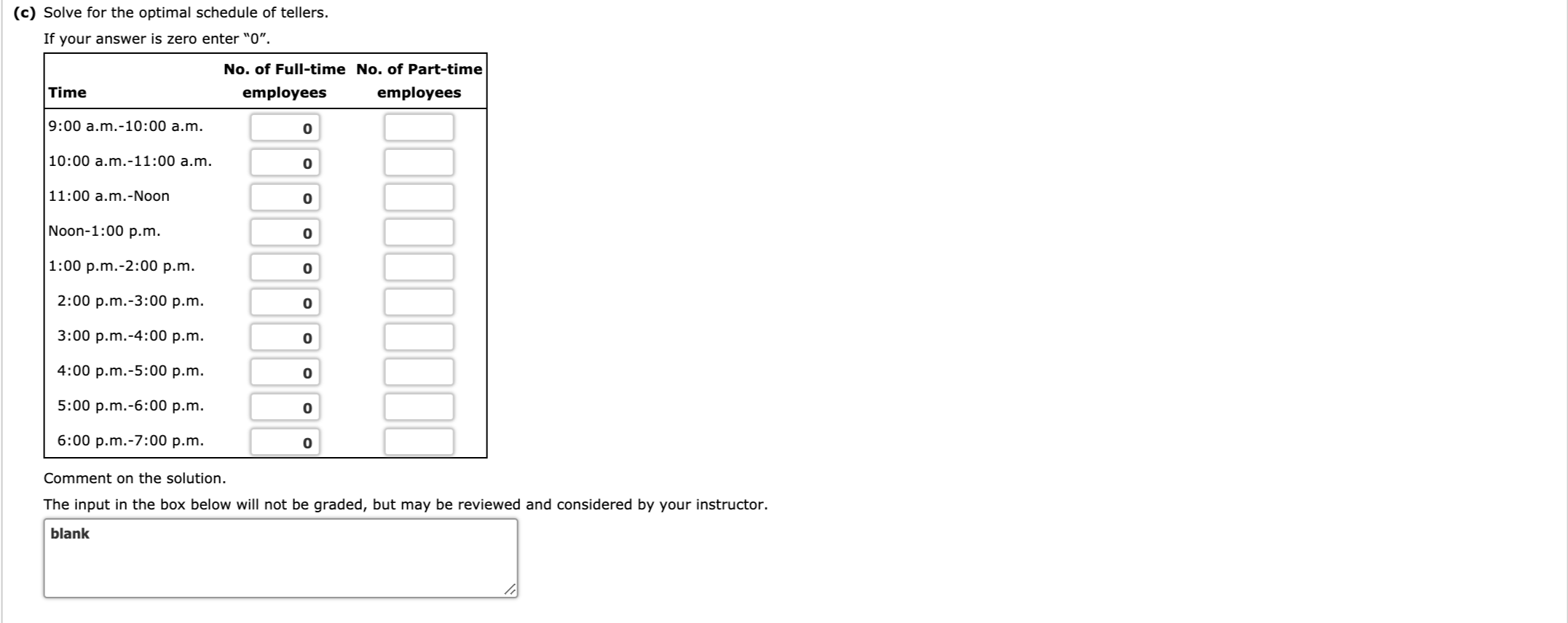
The bank is working to develop an efficient work schedule for full-time and part-time tellers. The schedule must provide for efficient operation of the bank, including adequate customer service, employee breaks, and so o 9:00 A.M. to 7:00 P.M. The number of tellers necessary to provide adequate customer service during each hour of operation is summarized here. Time No. of Tellers Time No. of Tellers 9:00 a.m.-10:00 a.m. 4 2:00 p.m.-3:00 p.m. 10:00 a.m.-11:00 a.m. 2 3:00 p.m.-4:00 p.m. 11:00 a.m.-Noon 7 4:00 p.m.-5:00 p.m. Noon-1:00 p.m. 11 5:00 p.m.-6:00 p.m. UT 1:00 p.m.-2:00 p.m. 7 6:00 p.m.-7:00 p.m. UT Each full-time employee starts on the hour and works a 4-hour shift, followed by a 1-hour break and then a 3-hour shift. Part-time employees work one 4-hour shift beginning on the hour. Considering salary and fringe be bank $15 per hour ($105 a day), and part-time employees cost the bank $8 per hour ($32 per day). (a) Formulate an integer programming model that can be used to develop a schedule that will satisfy customer service needs at a minimum employee cost. (Hint: Let x; = number of full-time employees coming on duty number of part-time employees coming on duty at the beginning of hour j.) If your answer is zero enter "0" and if the constant is "1" it must be entered in the box. Min 105 X9 105 X10 + 105 X11 + 32 y9 32 y10 + s.t. 1 x9 + 32 y11 + 0 x10 + 32 y12 + 32 y1 + 0 X11 + 1 y9 + 32 12 + o y10 + 32 y3 1 x9 + 0 y11 + 1 X10 + 0 y12 + o y1 + 0 x11 + 0 y2 + 1 y9 + 2 1 y10 + 0 y3 1 x9 + 0 y11 + 1 X10 + 0 y12+ 0 y1 + 1 X11 + 0 yz + 2 1 y9 + 1 y10 + 0 y3 1 x9 + 1 y11 + 1 X10 + 0 y12 + o y1 + 1 X11 + 0 y2 + 1 y9 + 0 y3 2 1 y10 + 1 y11 + 0 x9 + 1 X10 + 1 y12+ 0 y1 + 1 X11 + 0 y2 + 0 y9 + 0 3 2 1 y10 + 1 x9 + 1 y11 + + 0 x10 + 1 y1 + 1 X11 + 0 yz + 0 y9 2 + 0 y3 0 y10 + 1 y11 + 1 X9 1 X10 + 1 y12 + 1 y1 0 x11 + 1 y2 + 0 y9 0 3 2 + 0 y10 + 0 y11 + 1 X9 1 X10 + 1 y12 + 1 y1 + 1 X11 + 1 yz + 0 y9 + 1 y3 2 0 y10 + 0 y11 + 0 x9 + 1 X10 + 0 y12 + 1 y1 1 x11 + 1 yz + 0 y9 + 1 y3 2 0 y10 + o y11 + 0 x9 + 0 x10 + 0 y12 + 1 X11 + o y1 1 y2 + 0 y9 1 y3 2 0 y10 + xi, yj 2 0 and integer for i = 9, 10, 11 and j = 9, 10, 11, 12, 1, 2, 3 0 y11 + 0 y12 + 0 y1 + 0 y2 + 1 13 2(b) Solve the LP Relaxation of your model in part (a). If required, round your answers to the nearest whole number. If your answer is zero enter "0". X10 X11 y9 y10 y11 y12 y1 y2 y3 Total Cost: $(c) Solve for the optimal schedule of tellers. If your answer is zero enter "0". No. of Full-time No. of Part-time Time employees employees 9:00 a.m.-10:00 a.m. 0 10:00 a.m.-11:00 a.m. 0 11:00 a.m.-Noon Noon-1:00 p.m. 0 1:00 p.m.-2:00 p.m. 0 2:00 p.m.-3:00 p.m. 0 3:00 p.m.-4:00 p.m. 0 4:00 p.m.-5:00 p.m. 0 5:00 p.m.-6:00 p.m. 0 6:00 p.m.-7:00 p.m. 0 Comment on the solution. The input in the box below will not be graded, but may be reviewed and considered by your instructor. blank(d) After reviewing the solution to part (c), the bank manager realized that some additional requirements must be specified. Specifically, she wants to ensure that one full-time employee is on duty at all times and that t employees. Revise your model to incorporate these additional requirements, and solve for the optimal solution. If required, round your answers to the nearest whole number. If your answer is zero enter "0". The new optimal solution is as follows: No. of Full-time No. of Part-time Time employees employees 9:00 a.m.-10:00 a.m. 10:00 a.m.-11:00 a.m. 11:00 a.m.-Noon Noon-1:00 p.m. 1:00 p.m.-2:00 p.m. 2:00 p.m.-3:00 p.m. 3:00 p.m.-4:00 p.m. 4:00 p.m.-5:00 p.m. 5:00 p.m.-6:00 p.m. 6:00 p.m.-7:00 p.m. Total Cost: $