I would prefer pseudo code.

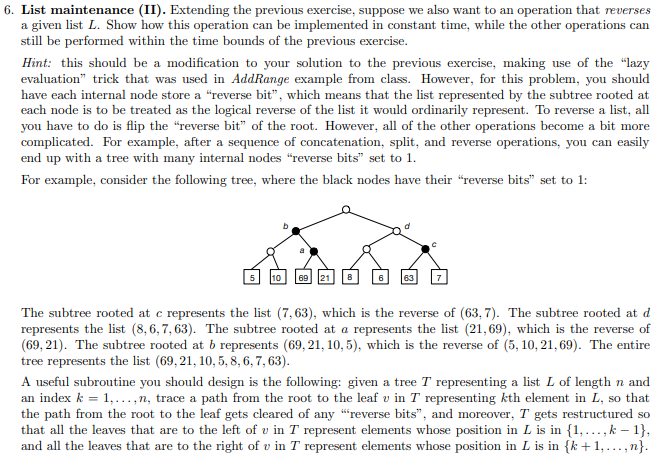
5. List maintenance (I). Consider the problem of maintaining a collection of lists of items on which the following operations can be performed: (i) Create a new list with one item. (ii) Given two lists L1 and L2, form their concatenation L, i.e., the list consisting of all items in L followed by all items in L2 (destroying Li and L2 in the process). (iii) Given a list L and a positive integer k, split L into two lists L1 and L2, where L1 consists of the first k items of L, and L2 the rest (L is destroyed in the process). (iv) Given a list L and a positive integer k, report the kth item in L. Describe a data structure and algorithms supporting these operations so that operation (i) takes constant time, and operations (ii)-(iv) can be performed in time (log n) (where n is the length of L). Hint: Use a variation on 2-3 trees, where the list elements are stored at the leaves in the same order as they appear in the list. For example, the following tree represents the list (5, 10, 69, 21, 8, 6,63,7): 6. List maintenance (II). Extending the previous exercise, suppose we also want to an operation that reverses a given list L. Show how this operation can be implemented in constant time, while the other operations can still be performed within the time bounds of the previous exercise. Hint: this should be a modification to your solution to the previous exercise, making use of the "lazy evaluation" trick that was used in AddRange example from class. However, for this problem, you should have each internal node store a "reverse bit", which means that the list represented by the subtree rooted at each node is to be treated as the logical reverse of the list it would ordinarily represent. To rev you have to do is flip the "reverse bit of the root. However, all of the other operations become a bit more complicated. For example, after a sequence of concatenation, split, and reverse operations, you can easily end up with a tree with many internal nodes "reverse bits" set to 1. For example, consider the following tree, where the black nodes have their "reverse bits" set to 1: The subtree rooted at c represents the list (7,63), which is the reverse of 63,7). The subtree rooted at d represents the list (8. 6, 7, 63). The subtree rooted at a represents the list (21,69), which is the reverse of (69,21). The subtree rooted at b represents (69, 21, 10,5), which is the reverse of 5, 10, 21,69). The entire tree represents the list 69.21, 10,5, 8, 6, 7, 63). A useful subroutine you should design is the following: given a tree T representing a list of length n and an index k = 1,...,n, trace a path from the root to the leaf u in T representing kth element in L, so that the path from the root to the leaf gets cleared of any "reverse bits", and moreover, T gets restructured so that all the leaves that are to the left of u in T represent elements whose position in L is in {1,..., k-1}, and all the leaves that are to the right of u in T represent elements whose position in L is in {k +1,...,n}. 5. List maintenance (I). Consider the problem of maintaining a collection of lists of items on which the following operations can be performed: (i) Create a new list with one item. (ii) Given two lists L1 and L2, form their concatenation L, i.e., the list consisting of all items in L followed by all items in L2 (destroying Li and L2 in the process). (iii) Given a list L and a positive integer k, split L into two lists L1 and L2, where L1 consists of the first k items of L, and L2 the rest (L is destroyed in the process). (iv) Given a list L and a positive integer k, report the kth item in L. Describe a data structure and algorithms supporting these operations so that operation (i) takes constant time, and operations (ii)-(iv) can be performed in time (log n) (where n is the length of L). Hint: Use a variation on 2-3 trees, where the list elements are stored at the leaves in the same order as they appear in the list. For example, the following tree represents the list (5, 10, 69, 21, 8, 6,63,7): 6. List maintenance (II). Extending the previous exercise, suppose we also want to an operation that reverses a given list L. Show how this operation can be implemented in constant time, while the other operations can still be performed within the time bounds of the previous exercise. Hint: this should be a modification to your solution to the previous exercise, making use of the "lazy evaluation" trick that was used in AddRange example from class. However, for this problem, you should have each internal node store a "reverse bit", which means that the list represented by the subtree rooted at each node is to be treated as the logical reverse of the list it would ordinarily represent. To rev you have to do is flip the "reverse bit of the root. However, all of the other operations become a bit more complicated. For example, after a sequence of concatenation, split, and reverse operations, you can easily end up with a tree with many internal nodes "reverse bits" set to 1. For example, consider the following tree, where the black nodes have their "reverse bits" set to 1: The subtree rooted at c represents the list (7,63), which is the reverse of 63,7). The subtree rooted at d represents the list (8. 6, 7, 63). The subtree rooted at a represents the list (21,69), which is the reverse of (69,21). The subtree rooted at b represents (69, 21, 10,5), which is the reverse of 5, 10, 21,69). The entire tree represents the list 69.21, 10,5, 8, 6, 7, 63). A useful subroutine you should design is the following: given a tree T representing a list of length n and an index k = 1,...,n, trace a path from the root to the leaf u in T representing kth element in L, so that the path from the root to the leaf gets cleared of any "reverse bits", and moreover, T gets restructured so that all the leaves that are to the left of u in T represent elements whose position in L is in {1,..., k-1}, and all the leaves that are to the right of u in T represent elements whose position in L is in {k +1,...,n}