Answered step by step
Verified Expert Solution
Question
1 Approved Answer
(i) You are given that u = (2,3,4) and v= (-1,-1,4). Find a vector x that is orthogonal to both u* and v. Also
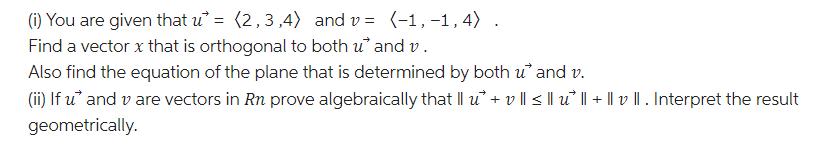
(i) You are given that u = (2,3,4) and v= (-1,-1,4). Find a vector x that is orthogonal to both u* and v. Also find the equation of the plane that is determined by both u* and v. (ii) If u and v are vectors in Rn prove algebraically that II u + v || | u || + || v II. Interpret the result geometrically.
Step by Step Solution
★★★★★
3.48 Rating (168 Votes )
There are 3 Steps involved in it
Step: 1
i You are given that 2 3 4 and 1 1 4 Find a vector that is orth og onal to both and ANS WER The vector 1 2 1 is orth og onal to both and WORK ING Let ...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Elementary Linear Algebra with Applications
Authors: Howard Anton, Chris Rorres
9th edition
471669598, 978-0471669593
